Практическая работа 23
Тема «Сумма бесконечно убывающей геометрической последовательности»
Цель: вывести формулу суммы бесконечной геометрической прогрессии; выработать практические навыки применения этой формулы при решении задании.
Ход работы:
1. Изучить материал к практической работе.
2. Выполнить практическую часть.
3. Выполнить тест.
Материал к практической работе
Бесконечно малые и бесконечно большие последовательности.
Определение. Последовательность {хn} называется бесконечно малой, если её предел равен нулю,
.
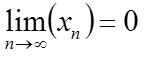Пример: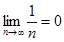 
, последовательность {хn}:1, 
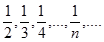, - бесконечно малая.
Определение. Последовательность {хn} называется бесконечно большой, если для любого положительного числа M, как бы велико оно ни было, существует такой номер N , что для всех {хn} с номерами n > N справедливо неравенство | х n | > M .
То есть, последовательность называется бесконечно большой, если её предел равен бесконечности,
.
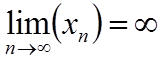Пример: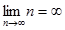 
, последовательность {zn}:1,2,3,4,5,…,n,… - бесконечно большая.
Заметим, что если последовательность {хn} является бесконечно малой (бесконечно большой), то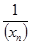 
- бесконечно большая (бесконечно малая).
Сумма бесконечной геометрической прогрессии
Рассмотрим бесконечную геометрическую прогрессию b1, b2, b3, …, bn,…
Пусть S1=b1,
S2=b1+b2,
S3=b1+b2+b3,
…………………….
Sn= b1+b2+b3+…+bn.
Получилась последовательность S1, S2, S3,…, Sn,… Как всякая последовательность она может сходиться или расходиться. Если последовательность Sn сходится к пределу S, то число S называют суммой геометрической прогрессии.
Пусть надо найти сумму n первых членов геометрической прогрессии:
Sn= b1+b2+b3+…+bn., то
.
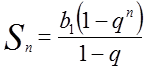Рассмотрим случай, когда знаменатель q геометрической прогрессии удовлетворяет неравенству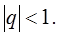 
Найдём: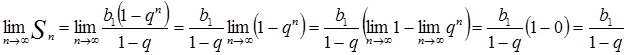 
.
(Так как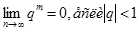 
)
Поэтому 
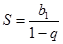
для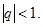 
Практическая часть
Задача 1. Найдите сумму геометрической прогрессии {bn}, если:
а) b1 = 3, q = 
; б) b1 = -1, q = 0,2;
в) 32, 16, 8, 4, 2, … ; г) 27, 9, 3, 1, , …
Задача 2. Вычислите:
а) 2 + 1 +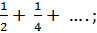 
б)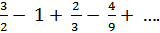 
Задача 3. Найдите знаменатель и сумму геометрической прогрессии {bn}, если:
а) b1 = - 2, b2 = 1; б) b1 = 3, b2 = .
Задача 4. Найдите знаменатель геометрической прогрессии {bn}, если:
а) S = 2, b1 = 3; б) S = - 10, b1 = - 5.
Задача 5. Найдите первый член геометрической прогресс {bn}, если:
а) S = 10, q = 0,1; б) S = - 3, q = - .
Задача 6. Найдите сумму геометрической прогрессии, если известно, что сумма первого и третьего ее членов равна 29, а второго и четвертого 11,6.
Задача 7. Вычислите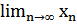 
, если:
а) хn =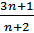 
; б) хn = 
.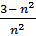