Оценка будущей стоимости денег по простым процентам
Чтобы рассчитать будущую стоимость вклада с начисленной суммой процентов, используется формула:
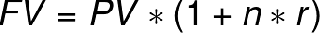
Формула простых процентов
Где n — число интервалов расчета процентных платежей, r — процентная ставка в виде десятичной дроби.
Для вложения в 1000 рублей , будущая стоимость вклада через 3 года (при ставке в 10%) будет составлять:
1000 x (1 + 3x0,1) = 1300 рублей
Вычисление будущей стоимости денег по сложным процентам
Вложенная в банк тысяча рублей по ставке 10% обладает текущей стоимостью в 1000 рублей. Процент, как мы помним из определения сложных процентов, начисляется на первоначальную сумму и полученный процент. Соответственно, через 3 года вклад составит:
| Год | Сумма на начало | Процент | Сумма на конец |
| 1 | 1000 | 0,1 * 1000 = 100 | 1000+100=1100 |
| 2 | 1100 | 0,1 * 1100 = 110 | 1100+110=1210 |
| 3 | 1210 | 0,1 * 1210 = 121 | 1210+121=1331 |
Расчеты необходимо делать по формуле:

Формула сложных процентов
Где FV - будущая стоимость, PV - текущая стоимость, r – процентная ставка, n- количество лет.
Если проценты будут начисляется чаще, чем ежегодно, то и будущая стоимость будет расти. Формула, позволяющая определить будущую стоимость по сложным процентам при выплатах, которые происходят чаще, чем ежегодно выглядит иначе.
В зависимости от того, насколько часто будут выплачиваться проценты, вы будете получать и разную будущую стоимость.
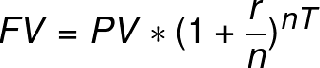
Формула сложных процентов с определенной частотой начисления процентов
Где Т - общее время вклада в годах, n - частота начисления процентов. Если начисления выполняются каждый месяц, то n=12, а если каждый день, то n=365
Дисконтирование
Операция, являющаяся обратной начислению сложных процентов - дисконтирование. Она позволяет рассчитать будущую стоимость денег сегодня, это позволяет определить, что выгоднее: взять в рассрочки или купить сегодня со скидкой. Именно этим вы обычно занимаетесь, когда оцениваете насколько эффективно будет вложение денег на период.
Допустим, необходимо определить какой размер капитала нужно вложить сегодня, чтобы через три года его стоимость составила 1330 рублей при 10 процентах годовых. Неизвестный размер капитала – текущая стоимость будущей стоимости в 1300 рублей. Определить текущую стоимость – вычислить дисконтирование.
Чтобы найти текущую стоимость, требуется будущую стоимость поделить на (1+ % ставка) такое количество раз, сколько лет берется для выполнения расчетов.
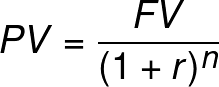
Формула дисконтирования с помощью сложных процентов
Допустим, что на протяжении 20 лет каждый год будут доходы, равные тысячи рублей. Расчет текущей стоимости этих денег можно увидеть в таблице.
| Год | Будущая стоимость | Текущая стоимость |
| 1 | 1000 | 1000/(1+0,1)^1=909,1 |
| 2 | 1000 | 1000/(1+0,1)^2=826,4 |
| 3 | 1000 | 1000/(1+0,1)^3=751,3 |
| ... | ||
| 10 | 1000 | 1000/(1+0,1)^10=385,5 |
| ... | ||
| 20 | 1000 | 1000/(1+0,1)^20=148,6 |
Процентная ставка для дисконтирования при экономическом анализе – доходы, которые можно получать при использовании разных инвестиционных возможностей.
К примеру, если существуют альтернативы: 3% годовых, при в кладе в государственные облигации, 4% годовых – банковский вклад или 10% годовых – в акции надежных компаний. При выполнении экономического анализа дисконтной ставкой как правило будет являться ставка в 10% годовых.
Для финансового анализа дисконтной ставкой является типичная процентная ставка, по которой компания может занимать капитал. Например, если банки осуществляют кредитование фирмы под 6%, то именно эта процентная ставка = дисконтной.
2. Практическая часть
Задача 1. 400 тыс. руб. инвестированы на год под сложные проценты по ставке 10 % годовых. Найдите наращенную сумму при начислении процентов:
а) по полугодиям;
б) ежеквартально.
Определите величину номинального и реального доход а, если годовой темп инфляции 8,5%.
Задача 2. На какой срок необходимо поместить денежную сумму под простую процентную ставку 8% годовых, чтобы она увеличилась в 2 раза?
Задача 3 . Определить реальную будущую стоимость инвестируемых денежных средств, если объем инвестиций - 100 тыс. рублей, период инвестирования - 3 года; номинальная ставка процента (с учетом инфляции) - 20 % в год; ожидаемый темп инфляции в год - 10 %.
Ситуационная задача 1
Вы получили неожиданную премию по итогам года в размере 150 тыс. руб.
На семейном совете было решено вложить их на ремонт в квартире, который предполагается делать через 3 года.
Каков будет ваш доход или потери в реальном выражении в следующих случаях.
1. Вы храните деньги дома «под матрасом» в течение 3 лет.
2. Вы кладете деньги на 3-летний депозит со ставкой 8,5% годовых (простые проценты).
3. Вы кладете деньги на годовой депозит со ставкой 7% годовых. Через год вы видите, что ставки выросли, и делаете новый вклад на 2 года под 9% годовых (простые проценты).
Ситуационная задача 2
У вас есть свободные денежные средства в сумме 25000 руб. Вы планируете разместить их в банке на 1 год.
Ставка по вкладу: в рублях — 7,5% годовых, в валюте — 3%.
Курс покупки/продажи доллара США в банке: на начало срока вложения денег — 62,75 / 65,30 руб.;
на конец срока (ожидаемый) — 67,30 / 69,10 руб.
Рассчитайте приращенную сумму в рублях и в валюте.
Проанализируйте, в какой валюте выгоднее вкладывать деньги в банк.
Сделайте вывод по ситуационным задачам.








