Тогда переменные называются главными переменными. Все остальные называются свободными.

Дата: 2025-06-02; Просмотры: 7

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Зиняков Георгий ИУ3-31 ОТЧЕТ

Исходные данные

Вариант 6

-150.6000 -8.2900 7.3900 8.5700 -484.3700 @ 3

7.7000 -77.0000 -0.8900 -2.6200 -355.0300 @ 5

4.3300 3.0300 146.8000 -4.2800 1077.1400 @ 7

8.7400 -2.6000 -1.2700 -112.4000 566.3300 @ -5

Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Описание метода

Пусть исходная система выглядит следующим образом

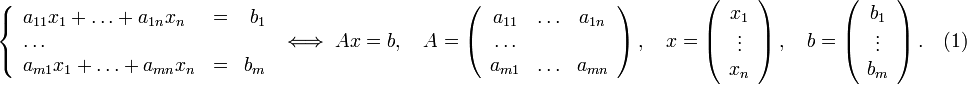
Матрица A называется основной матрицей системы, b — столбцом свободных членов.

Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

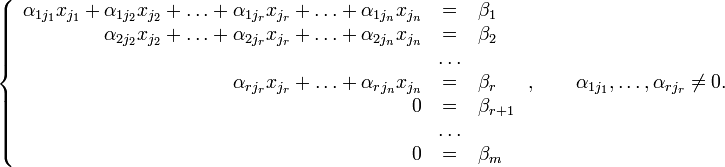
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных 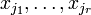^[3].

Тогда переменные 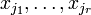называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число 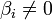, где i > r, то рассматриваемая система несовместна.

Пусть 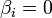для любых i > r.

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом 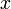( 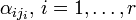, где 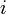— номер строки):

,
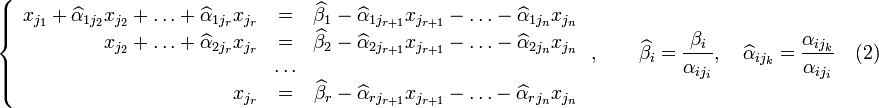где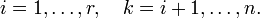

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

Текст программы

A=[-150.6000, -8.2900, 7.3900, 8.5700; 7.7000, -77.0000, -0.8900, -2.6200; 4.3300, 3.0300, 146.8000, -4.2800; 8.7400, -2.6000, -1.2700, -112.4000];

AOLD=A;

AOLD2=A;

F=[-484.3700; -355.0300; 1077.1400; 566.3300];

FOLD=F;

L1=[A(1,1) 0 0 0; A(2,1) 1 0 0; A(3,1) 0 1 0; A(4,1) 0 0 1]

for m=1:4,

buf=A(m, m);

if m==2

L2=[1 0 0 0; 0 A(2, 2) 0 0; 0 A(3,2) 1 0; 0 A(4,2) 0 1]

end

if m==3

L3=[1 0 0 0; 0 1 0 0; 0 0 A(3,3) 0; 0 0 A(4,3) 1]

end

if m==4

L4=[1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 A(4,4)]

end

for i=m:4,

A(m, i)=A(m, i)/buf;

end

F(m)=F(m)/buf;

for i=m+1:4,

if A(i, m)~=0

F(i)=F(i)-F(m)*A(i, m);

for j=m+1:4

A(i, j)=A(i, j)-A(m, j)*A(i, m);

end

end

end

for i=m+1:4,

A(i, m)=0;

end

end

x4 = F(4);

x3 = F(3) - A(3, 4)*x4;

x2 = F(2) - A(2, 4)*x4 - A(2, 3)*x3;

x1 = F(1) - A(1, 4)*x4 - A(1, 3)*x3 - A(1, 2)*x2;

F

A

L=L1*L2*L3*L4

ANEW=inv(L)*inv(A);

AOLD*ANEW

x1

x2

x3

x4

max=abs(A(1,1))+abs(A(1,2))+abs(A(1,3))+abs(A(1,4));

for i=2:4,

n1=abs(A(i,1))+abs(A(i,2))+abs(A(i,3))+abs(A(i,4));

if n1>max

max=n1;

end

end

n1=max

max=abs(A(1,1))+abs(A(2,1))+abs(A(3,1))+abs(A(4,1));

for i=2:4,

n2=abs(A(1,i))+abs(A(2,i))+abs(A(3,i))+abs(A(4,i));

if n2>max

max=n2;

end

end

noo=max

AOLD

for m=2:4

for i=m:4,

if AOLD(i, m-1)~=0

buf=AOLD(i, m-1);

for j=m-1:4,

AOLD(i, j) = AOLD(i, j) - AOLD(m-1, j)*buf/AOLD(m-1,m-1);

end

end

end

end

AOLD

det=1;

for i=1:4,

det=det*AOLD(i,i);

end

det

XNEW=[x1, x2, x3, x4];

B=[0; 0; 0; 0];

AOLD2

XNEW

for i=1:4,

for j=1:4,

B(i)=B(i)+AOLD2(i,j)*XNEW(j);

end

end

FOLD-B

Полученные данные

L1 =

-150.6000 0 0 0

7.7000 1.0000 0 0

4.3300 0 1.0000 0

8.7400 0 0 1.0000

L2 =

1.0000 0 0 0

0 -77.4239 0 0

0 2.7916 1.0000 0

0 -3.0811 0 1.0000

L3 =

1.0000 0 0 0

0 1.0000 0 0

0 0 146.9940 0

0 0 -0.8207 1.0000

L4 =

1.0000 0 0 0

0 1.0000 0 0

0 0 1.0000 0

0 0 0 -111.8388

F =

3.2163

4.9054

7.1399

-5.0000

A =

1.0000 0.0550 -0.0491 -0.0569

0 1.0000 0.0066 0.0282

0 0 1.0000 -0.0280

0 0 0 1.0000

L =

-150.6000 0 0 0

7.7000 -77.4239 0 0

4.3300 2.7916 146.9940 0

8.7400 -3.0811 -0.8207 -111.8388

ans =

1.0027 0.0567 0.0987 -0.0184

0.0009 0.9933 -0.0125 -0.0049

0.0020 -0.0047 0.9990 0.0665

-0.0001 -0.0065 -0.0030 1.0051

x1 =

3

x2 =

5

x3 =

7

x4 =

-5.0000

n1 =

1.1610

noo =

1.1131

AOLD =

-150.6000 -8.2900 7.3900 8.5700

7.7000 -77.0000 -0.8900 -2.6200

4.3300 3.0300 146.8000 -4.2800

8.7400 -2.6000 -1.2700 -112.4000

AOLD =

-150.6000 -8.2900 7.3900 8.5700

0.0000 -77.4239 -0.5122 -2.1818

0 0 146.9940 -4.1123

0 0 0 -111.8388

det =

-1.9169e+008

AOLD2 =

-150.6000 -8.2900 7.3900 8.5700

7.7000 -77.0000 -0.8900 -2.6200

4.3300 3.0300 146.8000 -4.2800

8.7400 -2.6000 -1.2700 -112.4000

XNEW =

3.0000 5.0000 7.0000 -5.0000

ans =

1.0e-012 *

-0.0568

0

-0.2274

-0.1137