Задача 6. Посчитать произведение чисел, вводимых с клавиатуры до тех пор, пока не встретится 0.
Решение. Здесь заранее не известно, сколько чисел будет введено, поэтому лучше воспользоваться циклом While:
Sub Произведение()
Dim a As Integer, P As Integer
a = InputBox("Введите ненулевое число")
P = 1
While a <> 0
P = P * a
a = InputBox("Введите число")
Wend
MsgBox (P)
End Sub
Обратите внимание, что «чистка» переменной Р заключается в присвоении ей значения 1, т.к. Р участвует в произведении P = P *a и обнуление Р при- вело бы к нулевому результату всей программы. Исполнение цикла продолжается до тех пор, пока не введен 0 в переменную а. В первой строке мы потребовали, чтобы вначале было введено ненулевое число. А что, если все-таки пользователь программы ввел 0? Тогда цикл не проработает ни разу и результат будет Р=1. Такой же результат будет, если ввели 1, а затем 0. Как различить эти случаи? «Защититься» от первого нуля можно, поставив, например, «оберегающий» оператор Until c проверкой на ноль:
Sub Произведение ()
Dim a As Integer, P As Integer
Do
a = InputBox("Введите ненулевое число")
Loop Until a <>0 P = 1
While a <> 0
P = P * a
a = InputBox("Введите число")
Wend
MsgBox (P)
End Sub
Здесь первый оператор цикла не позволит продолжить программу, если вводятся нули: условие выхода из цикла a<>0.
Задача 7. Найти максимальное из 10-ти чисел, вводимых с клавиатуры.
Решение. При нахождении максимума в последовательности значений, нужно определить начальное значение переменной (max), в которой будет храниться этот максимум. Затем каждое число в последовательности (здесь - каждое введенное число) сравнивается со значением max и, если это число превышает max, то оно теперь считается максимальным и поэтому заносится (присваивается) в max, стирая предыдущее значение. Таким образом, основной оператор алгоритма решения – это цикл, в котором тело составляют два действия: ввод нового значения и проверка, не является ли это значение максимальным (из тех, что уже были введены). По окончании цикла (когда все числа уже введены и проверены) в max будет находиться наибольшее из них. Что взять в качестве начального значения max? Верное решение – взять любое из анализируемой последовательности, например, первое. Неверное решение – взять «с потолка», например, 0. Ноль сгодится, если вводятся только положительные числа (тогда любое из них «закроет» первоначальный максимум). Но, если могут быть введены только отрицательные числа, то этот 0 и окажется максимальным, хотя и не был введен. Ответ будет неверным. Итак, возьмем в качестве начального значения первое из вводимых чисел и откроем цикл с проверкой оставшихся 9-ти чисел на максимум. Поскольку число шагов известно, проще воспользоваться циклом For:
Sub МаксЧисло()
Dim max As Single, a As Single ‘типпеременных – Single
max = InputBox("Введите число")
For i = 1 To 9
a = InputBox("Введите число")
If a > max Then
max = a
End If
Next
MsgBox (max)
End Sub
Аналогично решаются задачи на поиск минимума, нужно только заме- нить знак неравенства на < и переобозначить переменную (для ясности): вместо max взять, например, min.
Задачи для самостоятельной работы:
1. Найти максимальный из отрицательных элементов среди произвольных 20 чисел, вводимых с клавиатуры.
2. Найти первый отрицательный член последовательности sin(tg(n)) для n, изменяющегося так: n=1, 2, 3,…
3. Вычислить положительные значения функции y=sin(x)+4cos(x-2) для x, изменяющемся на отрезке [-15,10] с шагом 1.
4. Найти количество чисел, кратных трем, из последовательности, вводимой с клавиатуры до тех пор, пока не встретится ноль.
Лабораторная работа № 4. Итерации (рекуррентные соотношения) и вложенные циклы
Задачи такого типа можно представить как определение некоторой величины Y, которая является результатом последовательности вычислений Yi=F(Yi-1) , т.е. каждое последующее значение Y вычисляется на основе его предыдущих значений. Процесс заканчивается при достижении какого-либо условия или конкретного значения. Для решения подобных задач нужно понять закономерность образования каждого последующего значения, т.е. задать функцию (или выражение) F. Очевидно, что процесс вычисления является циклом и для начала проще всего определить его тело: какие действия повторяются, какие величины и на сколько изменяются на каждом шаге. После этого будет яснее условие продолжения (окончания) цикла.
Задача 8. Вычислить значение Y, определяемое формулой:
.
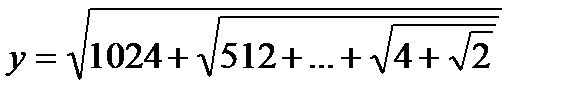Решение. Алгоритм будет понятнее, если представить числа в этом выражении как степени двойки:
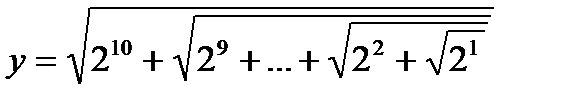
Вычисление Y можно организовать тогда, используя цикл из десяти шагов. На каждом шаге i выполняется операция: к 2i прибавляется значение, вычисленное на предыдущем шаге, и из результата извлекается квадратный корень. Таким образом, результат i-го шага: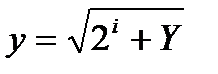 
Осталось только задать начальное значение Y=0. Программа тогда:
Sub Корень ( )
Dim Y As Single
Y=0
For i = 1 To 10
Y = (2^i + Y)^(1/2)
Next
MsgBox Y
End Sub
Здесь символ ^ означает операцию возведения в степень: ab в языке VBA можно представить как a^b , тогда и Öa (a в степени 1/2) есть a^(1/2).
Задача 9. Вычислить значение Y , определяемое формулой:
.
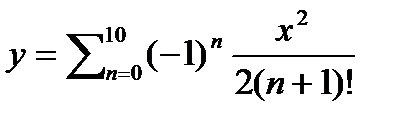Решение. Вычисление, очевидно, реализуется циклическим алгоритмом, состоящим из 11 шагов. На каждом шаге к сумме Y прибавляется очередной, Y i, элемент ряда: Y=Y+Yi. Сложность этой задачи можно понизить, если выявить зависимость каждого последующего Y i от предыдущего Yi-1 значения. Величина x от шага к шагу не изменяется, в такой постановке задачи ее просто нужно один раз ввести, например, с клавиатуры.
Итак, для всякого i от 0 до 10,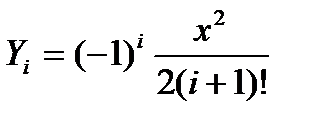 
. Соответственно 
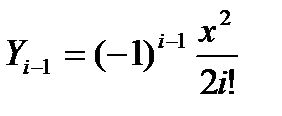. Разделим Y i на Yi-1 , учитывая, что, по определению факториала, (i + 1)! = i !(i +1). После сокращений получим: 
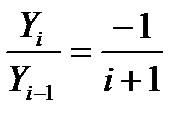, отсюда следует, что 
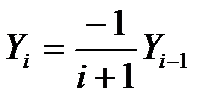. В суммируемой последовательности последний Y i +1 – это Y10 , а первый Yi - это Y0 . Вычислим это начальное значение, подставив в формулу для Yi вместо i –ноль: 
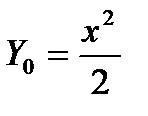. Окончательно, программа:
Sub MyY ( )
Dim Y As Single, yi As Single, x As Single
x = InputBox(“Введите значение х”)
yi = (x^2)/2 ‘значение начального –Y 0 элемента ряда
Y = yi ‘начальное значение суммы
For i = 1 To 10
yi = (-1/(i+1))*yi ‘считаем очередной Y i -й элемент
Y = Y + yi ‘считаем сумму
Next
MsgBox Y
End Sub
Отметим, что (частая ошибка!) замена двух операторов тела цикла на один: Y = Y +(-1/(i+1))*yi приведет к тому, что на каждом шаге цикла к сумме Y будет прибавляться одно и то же значение yi, равное Y0 , ведь yi тогда никак не изменяется. В программах, использующих зависимость i-го эле- мента в итерации от i-1-го, необходимо запоминать это предыдущее, вычисленное на (i-1)-м шаге значение, чтобы потом использовать именно его.
Задача 10. Для каждого числа b из 20-ти чисел, вводимых с клавиатуры определить наименьшее неотрицательное целое k такое, что b < 2 k .
Решение. Алгоритм составляет цикл из 20-ти шагов, на каждом из которых: вводится очередное число; проверяется, какую (наименьшую) степень двойки оно не превышает; выводится показатель этой степени. Как получить нужную степень двойки? Пусть число b введено. Начинаем процесс проверки с 20 , т.е. b< 20? Если да, процесс окончен, ответ k= 0. Если нет, проверяем 21 , т.е. b < 21? Если да, процесс окончен, ответ k = 1. Если нет, проверяем 22 , b < 22 ? И так до тех пор, пока не найдем нужное k. Таким образом, на каждом шаге внешнего цикла (ввод очередного числа) работает внутренний цикл, перечисляющий степени k двойки. Условие выхода из этого внутреннего цикла –число b больше или равно 2k . Программа:
Sub MinK ( )
Dim b As Integer, k As Integer
For i = 1 To 20 ‘внешний цикл вводит очередное b и печатает результат
b = InputBox("Введите целое число")
k = 0 ‘для каждого b начинаем поиск k с нуля!
While b >= 2 ^ k ‘внутренний цикл; условие цикла на каждом его шаге пересчитывается
k = k + 1 ‘увеличиваем показатель степени
Wend
MsgBox "Для b =" & CStr(b) & " k=" & CStr(k)
Next
End Sub
Здесь операция & склейки строк при выводе текста потребовала преобразования типов CStr из целого в строковый, т.к. она определена для аргументов- строк.
Задачи для самостоятельной работы:
1. Вычислить выражение: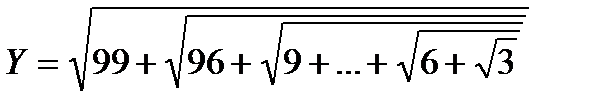 
2. Найти сумму бесконечного ряда с точностью до e>0: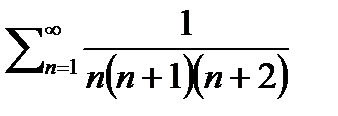 
.
3. Найти сумму k первых членов ряда: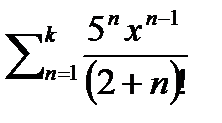 
.
4. Для каждого числа a из 20-ти чисел, вводимых с клавиатуры определить наибольшее целое k такое, что a > k3 .
Лабораторная работа № 5. Задачи с данными –одномерными (линейными) массивами