Определение уравновешивающей силы методом "жесткого рычага" Н. Е. Жуковского
Уравновешивающую силу Ру можно найти более коротким методом, предложенным Н.Е.Жуковским.
Теорема Н.Е.Жуковского о жестком рычаге. Если силу, приложенную к какой-либо точке звена плоского механизма, перенести параллельно самой себе в одноименную точку повернутого на 90° плана скоростей, то момент этой силы относительно полюса плана скоростей будет пропорционален ее мощности.
Мощность некоторой силы Fi , приложенной к точке механизма, имеющей скорость vi , может быть определена следующим образом
.
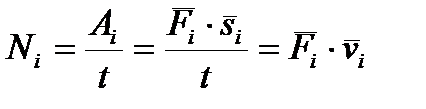Или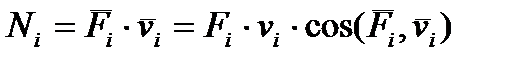 
. (2.8)
Следовательно, произведение силы и скорости точки ее приложения с учетом косинуса угла между направлениями этих векторов позволяет рассчитать значение мощности, развиваемой данной силой. Как раз эту процедуру и реализует теорема Н.Е.Жуковского.
На основании теоремы Жуковского представляется возможным определить уравновешивающую силу как движущую силу, необходимую для обеспечения равномерного движения входного звена.
Физический смысл метода "жесткого рычага" Н.Е.Жуковского заключается в том, что при установившемся режиме работы циклового механизма в любой момент времени должен выполняться баланс мощностей: мощность Nдв, поступающая в механизм за счет движущих сил, должна быть равна алгебраической сумме мощностей Ni, расходуемых силами, действующими на звенья механизма:
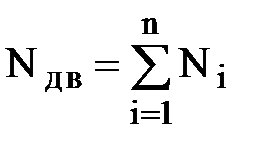. (2.9)
Для механизма, представленного на рис. 2.2, методика определения уравновешивающей силы будет состоять в следующем:
План скоростей механизма в анализируемом положении поворачивают на 90° ( желательно в ту сторону, чтобы одноименные точки плана скоростей и плана положений механизма максимально совпали).
К соответствующим точкам повернутого плана скоростей, рассматриваемого уже как "жесткая" неизменяемая фигура, прикладывают путем параллельного переноса все внешние активные силы: силы тяжести, силы инерции, силу полезного сопротивления и уравновешивающую силу. Точка приложения каждой силы на жестком рычаге должна быть определена по принципу подобия.
Составляется уравнение равновесия жесткого рычага с приложенными к нему силами в виде уравнения моментов относительно полюса т. рv, из которого определяется величина уравновешивающей силы Ру.
На рис. 2.3 представлен жесткий рычаг рассматриваемого механизма с приложенными к нему действующими силами.
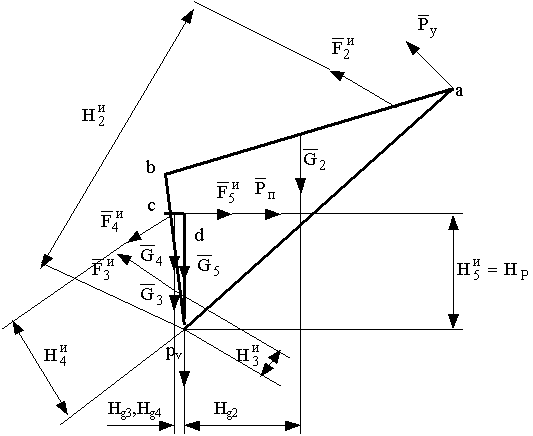
Рис. 2.3. "Жесткий рычаг" Н.Е. Жуковского
Уравнение равновесия рычага в виде суммы "моментов" действующих сил относительно полюса pv имеет вид
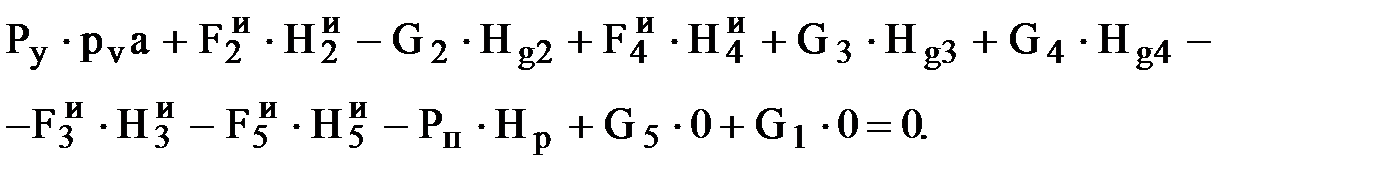
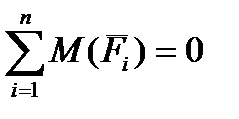; (2.10)
Из уравнения (2.10) уравновешивающая сила Ру
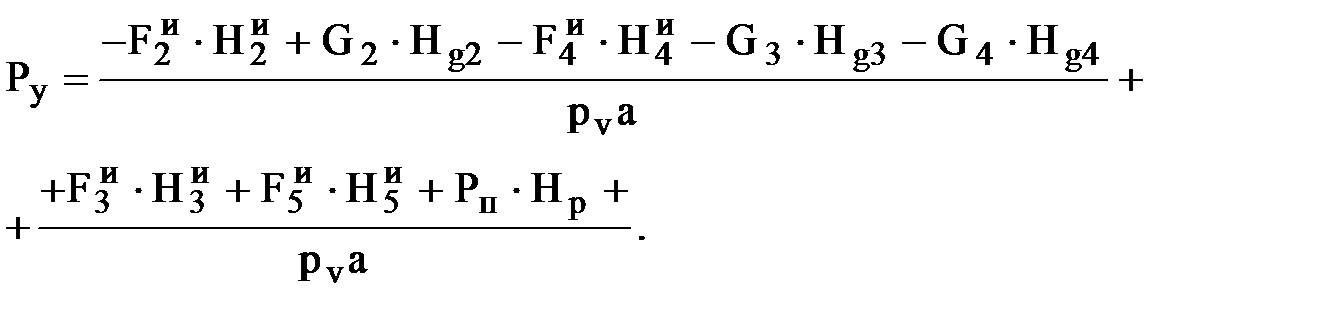
Сопоставление уравновешивающих сил, определенных из силового анализа и методом "жесткого рычага", позволяет осуществлять проверку и оценивать погрешность расчетов.