Сила инерции и точка ее приложения
Как уже было отмечено ранее, силы инерции звеньев могут быть приведены к главному вектору и главному моменту сил инерции:
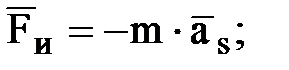
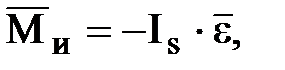 (1.1)
(1.1)
где 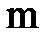 - масса звена;
- масса звена;
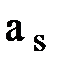 - ускорение центра масс звена;
- ускорение центра масс звена;
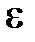 - угловое ускорение звена;
- угловое ускорение звена;
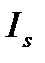 - момент инерции звена относительно оси, проходящей через центр масс.
- момент инерции звена относительно оси, проходящей через центр масс.
Сила инерции приложена к центру масс звена и направлена в сторону, противоположную направлению соответствующего линейного ускорения центра масс.
При поступательном линейном движении звена, например, ползуна, силы инерции приводятся к силе инерции, равной (рис.1.1,а):
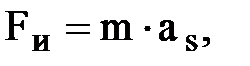 (1.2)
(1.2)
где as - ускорение центра масс звена.
При плоском движении силу инерции и момент сил инерции, действующие на звено, можно заменить одной силой, которая должна быть смещена параллельно силе инерции на плечо h (рис.1.1,б), определяемое из условия:
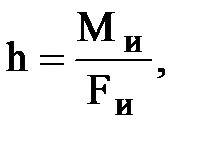 (1.3)
(1.3)
где 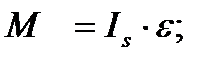
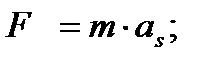
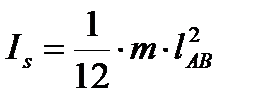 — момент инерции стержня относительно его середины. Причем момент перенесенной силы
— момент инерции стержня относительно его середины. Причем момент перенесенной силы 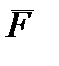 относительно центра масс должен иметь то же направление, что и момент сил инерции
относительно центра масс должен иметь то же направление, что и момент сил инерции 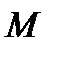 .
.
При вращательном движении сила инерции проходит через центр качания т.К (рис.1.1,в). Расстояние между центром масс и центром качания т.К определяется из выражения:
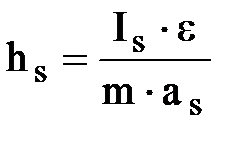 . (1.4)
. (1.4)
Если момент инерции вращающегося звена определен относительно оси вращения т.О
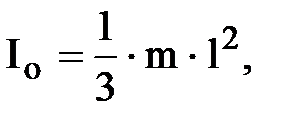 (1.5)
(1.5)
то плечо переноса силы инерции рассчитывается относительно т.О (рис.6.1,в): 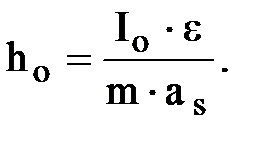 (1.6)
(1.6)
а) в)


 * * *
* * *
Рис.1.1. Частные случаи нахождения сил инерции:
а) поступательное линейное движение;
б) плоское движение;
в) вращательное движение
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В КИНЕМАТИЧЕСКИХ ПАРАХ. СИЛОВАЯ ОПРЕДЕЛИМОСТЬ СТРУКТУРНЫХ ГРУПП Л.В.АССУРА
Для определения реакций в кинематических парах используется принцип Д¢Аламбера или метод кинетостатики: составляются уравнения равновесия всех действующих сил и сил инерции. Для плоского механизма записываются следующие уравнения равновесия:

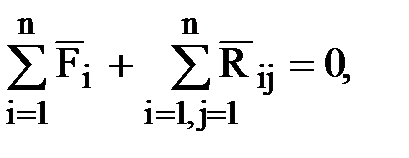 ( 1.7)
( 1.7)
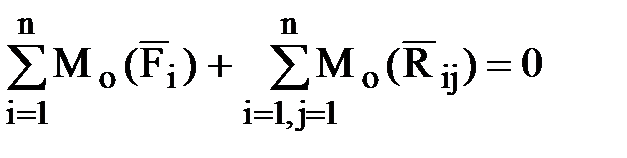 , (1.8)
, (1.8)
где 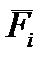 - i-тые внешние активные силы вместе с силами инерции;
- i-тые внешние активные силы вместе с силами инерции;
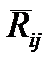 - вектор реакций связей ( реакция i-того звена на j-тое);
- вектор реакций связей ( реакция i-того звена на j-тое);
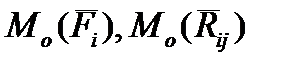 - моменты выше указанных сил.
- моменты выше указанных сил.
В проекциях на оси координат уравнения равновесия (6.7) и (6.8) имеют вид:
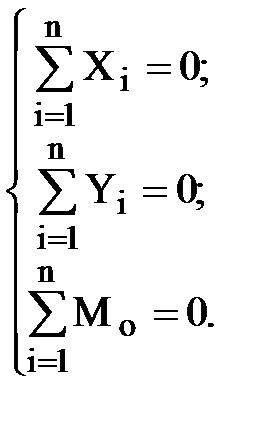
 (1.9)
(1.9)
Следовательно, для плоского механизма можно составить три условия (уравнения) его кинетостатического равновесия. Количество же неизвестных сил, подлежащих определению, значительно превышает это количество уравнений, следовательно система (6.9) является многократно статически неопределимой. Так, например, для механизма, представленного на рис. 6.2 в число неизвестных сил входят:
- составляющие реакции в опоре О1 (неподвижный шарнир) 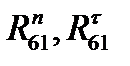 ;
;
- составляющие реакции в опоре О2 (неподвижный шарнир) 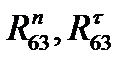 ;
;
- реакция направляющей ползуна 5 R65;
- движущая сила Ру, приложенная к ведущему звену (кривошипу 1).
Таким образом, количество неизвестных превышает количество уравнений, и система (6.9) является дважды статически неопределимой.
Решение задачи силового анализа становится выполнимой при разделении механизма  на структурные группы Л.В.Ассура, которые обладают силовой определимостью.
на структурные группы Л.В.Ассура, которые обладают силовой определимостью.
В качестве примера рассмотрим силовой расчет плоского рычажного механизма, изображенного на рис. 1.2. Для этого его условно разделяют структурные группы, включая начальный механизм (ведущее звено со стойкой). Силовой анализ начинают с наиболее удаленной от ведущего звена структурной группы, а заканчивают расчетом начального механизма.
Будем считать, что для рассматриваемого положения механизма уже выполнен кинематический анализ, а следовательно, определены силы и моменты сил инерции, осуществлен перенос сил инерции для учета действующих моментов сил инерции, а также рассчитаны силы тяжести всех звеньев 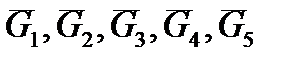 и сила полезного сопротивления
и сила полезного сопротивления 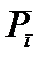 .
.
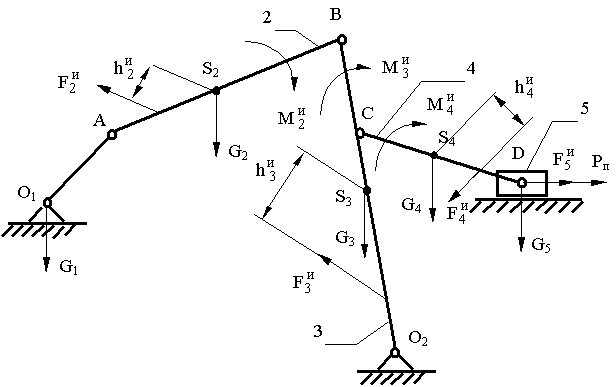
Рис.1.2. Схема механизма
Выделяем первую структурную группу, состоящую из звеньев 5 и 4, и рассматриваем ее кинетостатическое равновесие (рис.1.3,а).
а) б) mF=_Н/мм
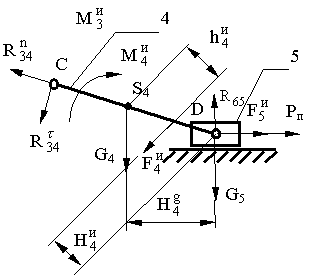
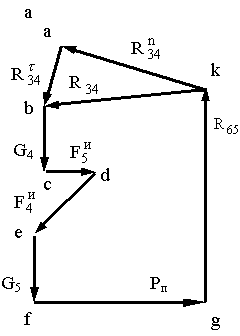
Рис.1.3. Силовой анализ I-ой структурной группы:
а) схема нагружения; б) план сил
На нее действуют известные силы 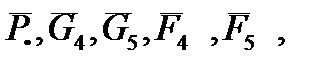 момент сил
момент сил 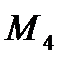 и неизвестные реакции
и неизвестные реакции 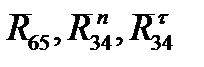 . Для исключения из расчета момента сил инерции
. Для исключения из расчета момента сил инерции 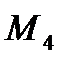 , но обеспечения его действия силу инерции
, но обеспечения его действия силу инерции 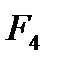 переносят на плечо
переносят на плечо 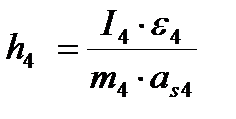
с учетом масштаба построения 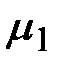 в ту сторону, чтобы относительно центра масс звена т. S4 момент действовал в ту же сторону, что и исходный.
в ту сторону, чтобы относительно центра масс звена т. S4 момент действовал в ту же сторону, что и исходный.
Уравнение равновесия для структурной группы
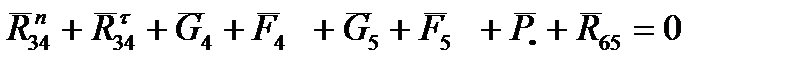 . ( 1.10 )
. ( 1.10 )
Тангенцильную составляющую 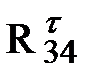 определяют из условия равновесия звена 4. Для этого составляют уравнение моментов относительно точки D:
определяют из условия равновесия звена 4. Для этого составляют уравнение моментов относительно точки D:
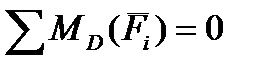 ;
; 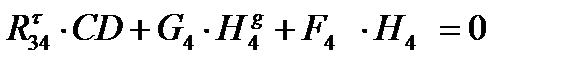 . (1.11)
. (1.11)
Откуда
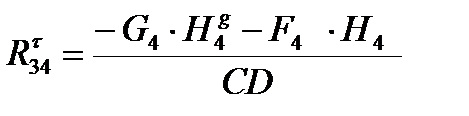 .
.
Неизвестные реакции 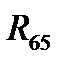 и
и 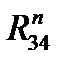 , а также полную реакцию
, а также полную реакцию 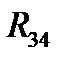 определяют из плана сил (рис. 6.3,б), построенного на основании уравнения равновесия (6.10). Для этого, выбрав масштаб mF (Н/мм), проводим вектора, изображающие силы
определяют из плана сил (рис. 6.3,б), построенного на основании уравнения равновесия (6.10). Для этого, выбрав масштаб mF (Н/мм), проводим вектора, изображающие силы 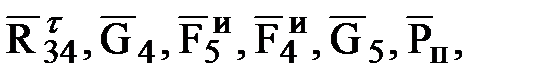 модули которых равны
модули которых равны
(ab)= 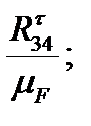 (bc)=
(bc)= 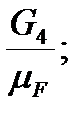 (cd)=
(cd)= 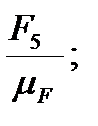 (de)=
(de)= 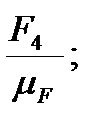 (ef)=
(ef)= 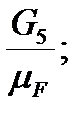 (fg)=
(fg)= 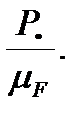
Линии действия векторов 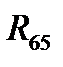 и
и 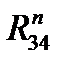 проводим соответственно через конец вектора
проводим соответственно через конец вектора 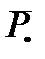 и начало вектора
и начало вектора 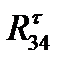 . Точка пересечения этих линий (т.д) определяет отрезки (gk) и (ka), изображающие вектора искомых сил
. Точка пересечения этих линий (т.д) определяет отрезки (gk) и (ka), изображающие вектора искомых сил
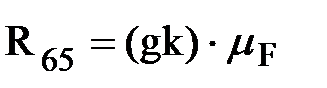 ;
; 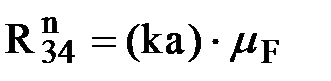 .
.
Полная реакция 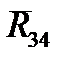 определится как векторная сумма
определится как векторная сумма  и
и 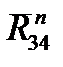 . Ее величина будет равна
. Ее величина будет равна
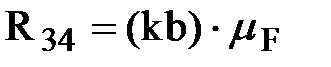 .
.
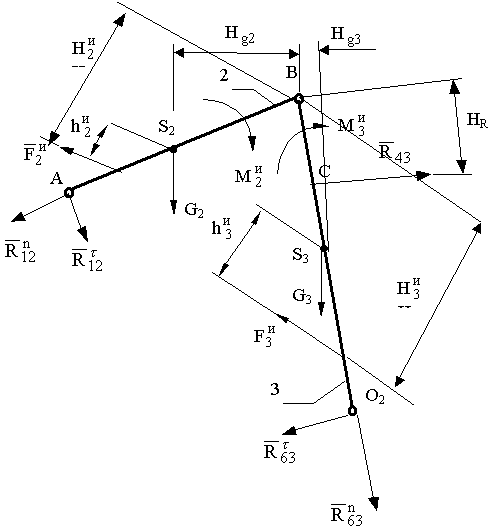
Продолжая силовой анализ механизма, выделяем следующую, вторую структурную группу, состоящую из звеньев 2 и 3, и рассматриваем её равновесие (рис.2.1,а). На нее действуют известные силы 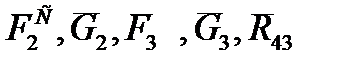 , причем
, причем 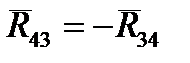 , моменты сил инерции
, моменты сил инерции 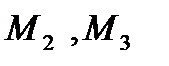 , а также неизвестные реакции
, а также неизвестные реакции 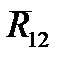 и
и 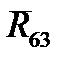 , которые разложим на составляющие
, которые разложим на составляющие 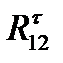 ,
, 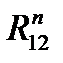 ,
, 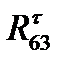 ,
, 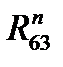 (нормальные составляющие направим вдоль соответствующих звеньев, а тангенциальные — перпендикулярно им). Уравнение равновесия для данной структурной группы будет иметь вид:
(нормальные составляющие направим вдоль соответствующих звеньев, а тангенциальные — перпендикулярно им). Уравнение равновесия для данной структурной группы будет иметь вид:
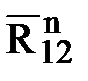 +
+ 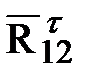 +
+ 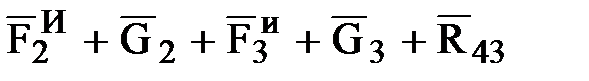 +
+ 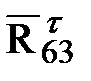 +
+ 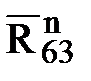 = 0. (2.1)
= 0. (2.1)
Тангенциальные составляющие 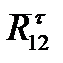 и
и 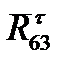 определяют из рассмотрения равновесия каждого звена 2 и 3 в отдельности. Для этого составляют уравнение моментов всех сил относительно точки B
определяют из рассмотрения равновесия каждого звена 2 и 3 в отдельности. Для этого составляют уравнение моментов всех сил относительно точки B
а)
б)
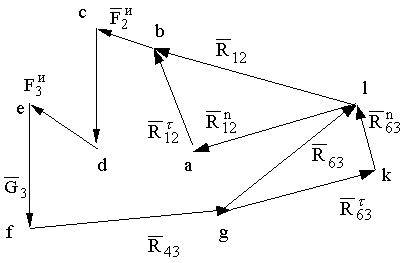
Рис. 2.1. Силовой анализ II- ой структурной группы:
а) схема нагружения; б) план сил
для звена 2:
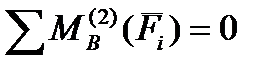 ;
; 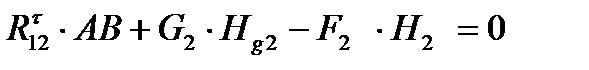 (1.2)
(1.2)
- для звена 3:
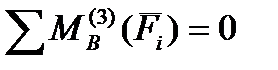 ;
; 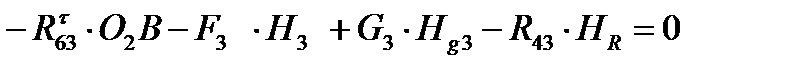 .
.  (1.3)
(1.3)
Из уравнения (7.2) определяем

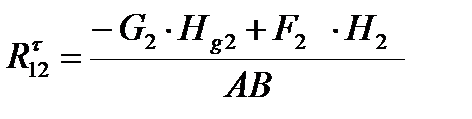 ;
;
а из уравнения (7.3) 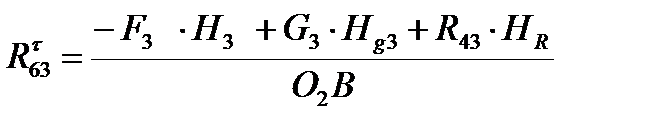 .
.
Неизвестные составляющие реакций 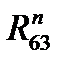 и
и 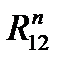 , а также полные реакции
, а также полные реакции 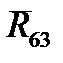 и
и 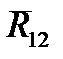 находим из плана сил второй структурной группы (рис. 1.1,б), построенного на основании уравнения равновесия (1.1). Для построения плана сил выбираем масштаб mF (Н/мм) и проводим вектора, изображающие силы
находим из плана сил второй структурной группы (рис. 1.1,б), построенного на основании уравнения равновесия (1.1). Для построения плана сил выбираем масштаб mF (Н/мм) и проводим вектора, изображающие силы 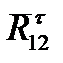 ,
, 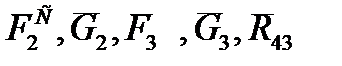 ,
, 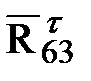 , модули которых равны
, модули которых равны
(ab)= 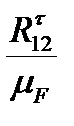 ; (bc)=
; (bc)= 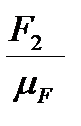 ; (cd)=
; (cd)= 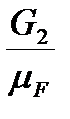 ; (de)=
; (de)= 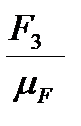 ; (ef)=
; (ef)= 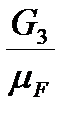 ; (fg)=
; (fg)= 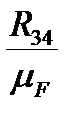 ; (gk)=
; (gk)= 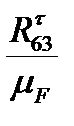 .
.
Линии действия векторов 
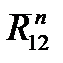 и
и 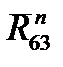 проводим соответственно через начало вектора
проводим соответственно через начало вектора 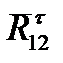 и конец вектора
и конец вектора 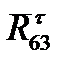 . Точка пересечения этих линий определит отрезки ((la) и (kl), изображающие искомые составляющие
. Точка пересечения этих линий определит отрезки ((la) и (kl), изображающие искомые составляющие 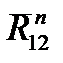 и
и 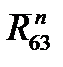 . Их величины будут равны
. Их величины будут равны
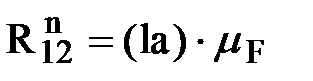 ;
; 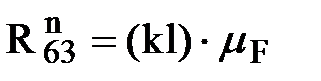 .
.
Полные реакции 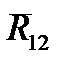 и
и 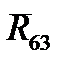 могут быть получены векторным сложением нормальных и тангенциальных составляющих (соответственно вектора (lb) и (gl)), а их величины определены по формулам
могут быть получены векторным сложением нормальных и тангенциальных составляющих (соответственно вектора (lb) и (gl)), а их величины определены по формулам 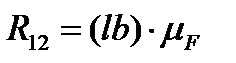 ;
; 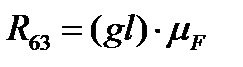 .
.
Затем переходим к силовому анализу начального механизма (рис.1.2,а). Считаем, что ведущее звено 1 вращается равномерно, а его центр масс за счет противовеса лежит на оси вращения. Тогда 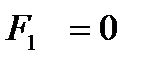 и
и 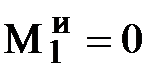 , и на кривошип 1 будут действовать следующие силы:
, и на кривошип 1 будут действовать следующие силы: 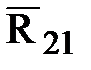 , причем
, причем 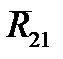 =-
=- 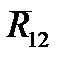 ,
, 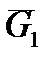 ,
, 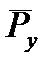 ,
, 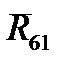 . Сила
. Сила 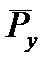 , приложенная в т.А перпендикулярно кривошипу , называется уравновешивающей и возникает в результате действия крутящего момента, передаваемого от электродвигателя, и поэтому относится к категории движущих сил.
, приложенная в т.А перпендикулярно кривошипу , называется уравновешивающей и возникает в результате действия крутящего момента, передаваемого от электродвигателя, и поэтому относится к категории движущих сил.
Уравнение равновесия начального механизма:
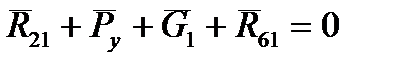 . (2.4)
. (2.4)
а)  б)
б) 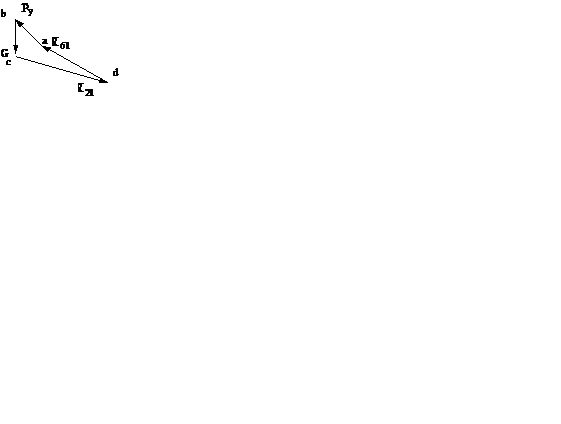
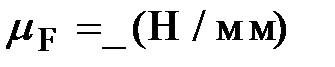
Рис. 2.2. Силовой анализ начального механизма:
а) схема нагружения; б) план сил
Уравновешивающую силу 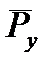 находим из уравнения моментов относительно точки О1
находим из уравнения моментов относительно точки О1
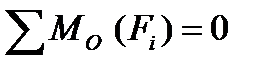 ;
; 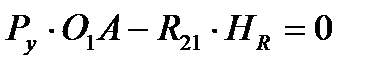 . (2.5)
. (2.5)
Откуда
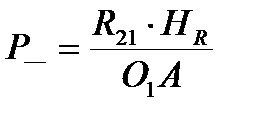 . (2.6)
. (2.6)
Уравновешивающий момент на кривошипе
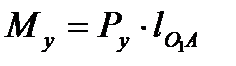 . (2.7)
. (2.7)
Величину и направление реакции стойки на кривошип 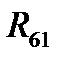 найдем из плана сил (рис.2.2,б), построенного на основании уравнения равновесия (2.4) в выбранном масштабе mF. Его величина
найдем из плана сил (рис.2.2,б), построенного на основании уравнения равновесия (2.4) в выбранном масштабе mF. Его величина
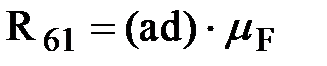 .
.
Таким образом, в результате силового анализа определены величины и направления реакций в кинематических парах, а также уравновешивающая сила.








