5. Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Вариант № профиль.
1. Килограмм орехов стоит 75 рублей. Маша купила 4 кг 400 г орехов. Сколько рублей сдачи она должна получить с 350 рублей?
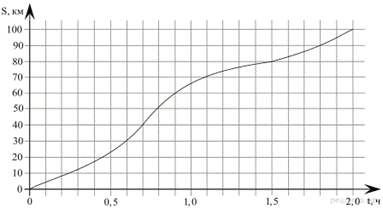
2. На рисунке показан график движения автомобиля по маршруту. На оси абсцисс откладывается время (в часах), на оси ординат — пройденный путь (в километрах). Найдите среднюю скорость движения автомобиля на данном маршруте. Ответ дайте в км/ч.
3. 
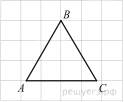На клетчатой бумаге с размером клетки 1 
1 изображён равносторонний треугольник. Найдите радиус описанной около него окружности.
4. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
5. Решите уравнение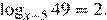 
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
6. 
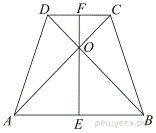В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
7. 
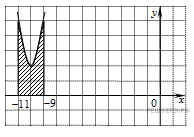На рисунке изображён график функции y = f(x). Функция 
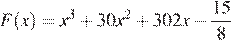— одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.
8. В кубе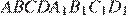 
точка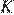 
— середина ребра 
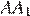, точка 
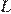— середина ребра 
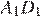, точка 
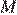— середина ребра 
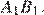Найдите угол 
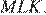Ответ дайте в градусах.
9. Найдите значение выражения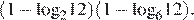 
10. Скорость колеблющегося на пружине груза меняется по закону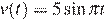 
(см/с), где t – время в секундах. Какую долю времени из первой секунды скорость движения была не менее 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
11. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20 000 рублей, через два года был продан за 15 842 рублей.
12. Найдите абсциссу точки максимума функции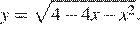 
13. а) Решите уравнение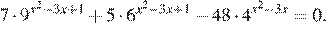 
б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].
14. В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 4, точка N — середина ребра AC, точка O центр основания пирамиды, точка P делит отрезок SO в отношении 3 : 1, считая от вершины пирамиды.
а) Докажите, что прямая NP перпендикулярна прямой BS.
б) Найдите расстояние от точки B до прямой NP.
15. Решите систему неравенств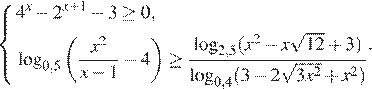 
16. На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD.
а) Докажите, что треугольник DCL равнобедренный.
б) Известно, что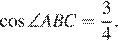 
В каком отношении прямая DL делит сторону AB?
17. На каждом из двух заводов работает по 100 человек. На первом заводе один рабочий изготавливает за смену 3 детали А или 1 деталь В. На втором заводе для изготовления t деталей (и А, и В) требуется t2 человеко-смен. Оба завода поставляют детали на комбинат, где собирают изделие, причем для его изготовления нужна 1 деталь А и 3 детали В. При этом заводы договариваются между собой изготавливать детали так, чтобы можно было собрать наибольшее количество изделий. Сколько изделий при таких условиях может собрать комбинат за смену?