%Основной комментарий
%Дополнительный комментарий
Тело файла с любыми выражениями
Особенности файлов-сценариев состоят в следующем:
–они не имеют входных и выходных аргументов;
–работают с данными из рабочей области;
–в процессе выполнения не компилируются;
–представляют собой зафиксированную в виде файла последовательность операций, полностью аналогичную той, что используется в сессии при работе в командном окне.
Основным комментарием является первая строка текстовых комментариев, а дополнительным – последующие строки. Основной комментарий выводится при выполнении команд lookfor и help-имя_каталога. Полный комментарий выводится при выполнении команды help-Имя_файла.
Создание m-файла сценария производится путем копирования заданной последовательности команд из Command Window, размещением ее в окне редактора, вызываемом последовательностью File - New - BlankM - File и сохранением ее под некоторым именем.
Использование m-файла-сценария состоит в вызове его в заданное место Command Window для выполнения определяемых им действий.
М-файл-функция является типичным объектом языка программирования системы Matlab. Одновременно он является полноценным модулем с точки зрения структурного программирования, поскольку содержит входные и выходные параметры и использует аппарат локальных переменных. Структура такого модуля с одним выходным параметром выглядит следующим образом:
functionvаг = f_name(Список_параметров)
%Основной комментарий
%Дополнительный комментарий
Тело файла с любыми выражениями
vаг=выражение
М-файл-функция имеет следующие свойства:
– он начинается с объявления function, после которого указывается имя переменной var – выходного параметра, имя самой функции и список ее входных параметров;
– функция выдает значение и может использоваться в виде
name(список_параметров)
в математических выражениях;
–все переменные, имеющиеся в теле файла-функции, являются локальными , т.е. действуют только в пределах тела функции;
–файл-функция является самостоятельным программным модулем, который общается с другими модулями через свои входные и выходные параметры;
–правила вывода комментариев те же, что у файлов-сценариев;
–файл-функция служит средством расширения системы Matlab;
–при обнаружении файла-функции он компилируется и затем исполняется, а созданные машинные коды хранятся в рабочей области системы Matlab.
Последняя конструкция vаг = выражение вводится, если требуется, чтобы функция выдавала результат вычислений.
Пример 5. Файл - функция
function r=randint(m,n)
%RANDINT случайная матрица с целыми элементами.
%randint(m,n) возвращает матрицу mxn с целыми
%элемента м и между 0 и 9.
a =floor(10*rand(m,n));
Пример 6. Более общий вид файл-функции
function r=randint(m,n,a,b)
%RANDINT случайная матрица с целыми элементами.
%randint(m,n)возвращает матрицу mxn с целыми
%элементами между 0 и 9.
%rand(m,n,a,b) возвращает матрицу с целыми
%элементами в диапазоне между целыми a и b.
ifnargin<3,a =0;b =9;end
r =floor((b-a+1)*rand(m,n))+a;
Этот текст должен быть записан на диск в виде файла с именем randint.m (в соответствии с именем функции – это обязательное условие для функции).
Первая строка функции – объявление имени функции, входные аргументы, выходные аргументы. Без такой строки весь следующий файл является программой, или сценарием, а не функцией. Так, например, оператор
z =randint(4,5)
приведет к передаче чисел 4 и 5 переменным m и n, а выходной результат будет передан переменной z. Поскольку переменные в файле-функции локальные, их имена никак не влияют на имена и значения переменных в текущей рабочей области Matlab.
Приведенная форма файла-функции характерна для функции с одним выходным параметром. Если выходных параметров больше, то они указываются в квадратных скобках после слова function. При этом структура модуля имеет следующий вид:
function[vаг1,vаг2,...]=f_namе (список_параметров)
%Основной комментарий
%Дополнительный комментарий
Тело файла с любыми выражениями
var1-выражение
Такая функция во многом напоминает процедуру. Ее нельзя слепо использовать непосредственно в математи-ческих выражениях, поскольку она выдает не единственный результат, а множество результатов – по числу выходных параметров. Если функция, имеющая несколько выходных параметров, входит в состав математического выражения, для вычислений в выражении будет использован первый из выходных параметров. Это зачастую ведет к ошибкам в вычислениях. Поэтому, как отмечалось, данная функция используется как отдельный элемент программ в виде
[varl,var2, …] = namе (Список_параметров).
После такого вызова выходные переменные varl, var2, … становятся определенными и их можно использовать в последующих математических выражениях и иных сегментах программы. Если функция используется в виде
f_namе (список_параметров),
то выдается значение только для первого выходного параметра – переменной varl. Приведенная далее функция, которая вычисляет наибольший общий делитель двух целых чисел с помощью алгоритма Евклида, иллюстрирует также использование функции вывода сообщений об ошибках.
Пример 7. Файл-функция с двумя параметрами
function a=gcd(a,b)
%GCD Наибольший общий делитель.
%gcd(a,b) является наибольшим общим делителем
%целых чисел a и b,оба не равны нулю.
a =round(abs(a));b =round(abs(b));
if a ==0 &b ==0
error(’gcd не определена, если оба числа равны нулю ’)
else
while b ~=0
r =rem(a,b);
a=b;b=r;
end
end
Создание m-файла функции производится в окне редактора, вызываемом последовательностью File - New - Function - M - File и сохранением ее под некото-рым именем.
Использование m-файла функции состоит в вызове его по имени функции в заданное место Command Window для выполнения определяемых ею действий. При этом значения передаваемых функции параметров должны быть определены заранее.
Рабочая область системы Matlab Workspace – это область памяти, в которой размещены переменные системы. Содержимое этой области можно просмотреть из командной строки с помощью команд who и whos. Различие между этими командами состоит в следующем:
– who– выводит только имена переменных;
–whos– выводит дополнительно информацию о размерах массивов и типе переменной.
Сохранение переменных рабочей области. Команда Save Workspace As … меню File либо команда save fname, набранная в командном окне позволяет сохранить содержимое рабочей области в двоичном m-файле, который можно в дальнейшем вызвать командой Open из меню главного окна, либо командой load из командного окна.
Загрузка рабочей области. Команда Open меню File или команда load, набранная в командном окне позволяет загрузить m-файл, который был ранее сохранен с помощью команды save. При загрузке m-файла новые значения одноименных переменных будут записаны взамен старых. Если m-файл имеет расширение, отличающееся от .mat, то необходимо использовать флаг –mat; в противном случае MATLAB будет считать форматом файла ASCII-формат.
Загрузка файлов данных в ASCII-формате. Команда load позволяет выполнять импорт файлов данных в ASCII-формате; она преобразует содержимое файла в переменную с именем файла только без расширения. Например, применение команды load tides.dat создает в рабочей области системы Matlab переменную с именем tides. Если исходный файл в ASCII-формате имеет m строк с n значениями в каждой строке, то результатом будет массив чисел размера m×n.
Для сохранения или загрузки последовательности файлов, имена которых имеют общий корень и дополнительный целочисленный суффикс, необходимо использовать структуру цикла.
Например, следующая конструкция позволяет сохранить квадраты чисел от 1 до 10 в файлах с именами data1, …, data10:
file = 'data';
fori = 1:10
j = i.^2;
save([file int2(i)],'j');
end
Использование группового символа. Команды load и save допускают использование группового символа (*) в качестве замены ряда символов в шаблоне имени переменной.
Например, команда save rundate x* сохраняет все переменные, имена которых начинаются с символа x в файле с именем rundata.mat.
Точно также команда load testdata ex1*95 загружает все переменные, имена которых начинаются с символов 'ex1' и заканчиваются символами '95', независимо от того, какие символы размещены между ними.
Пример 8. Использование рабочего пространства Matlab.
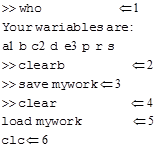
Комментарии к вычислениям:
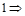 Команда вывода имен всех переменных рабочего пространства.
Команда вывода имен всех переменных рабочего пространства.
 Команда удаления переменной из рабочего пространства.
Команда удаления переменной из рабочего пространства.
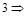 Команда сохранения рабочего пространства в дисковом файле под заданным именем.
Команда сохранения рабочего пространства в дисковом файле под заданным именем.
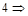 Команда очистки рабочего пространства.
Команда очистки рабочего пространства.
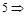 Команда загрузки рабочего пространства из ранее сохраненного файла.
Команда загрузки рабочего пространства из ранее сохраненного файла.
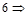 Команда очистки командного окна (рабочее пространство не изменяется).
Команда очистки командного окна (рабочее пространство не изменяется).
В результате сохранения рабочего пространства на диске создается файл с заданным именем (может быть произвольным) и расширением mat. Сохранение рабочего пространства можно выполнить через меню командного окна File пункт Save workspaceas …
В командном окне есть возможность вернуть в командную строку ранее введенные команды, они запоминаются в специальной области памяти, называемой стеком команд. Для этого используются клавиши «стрелка вверх» и «стрелка вниз». Клавиша «стрелка вверх» позволяет вывести предыдущие команды в порядке обратном их вводу. Клавиша «стрелка вниз» осуществляет прокрутку команд в противоположном направлении.
Создание графиков. Для построения двумерных графиков используются функции plot (в декартовой системе координат) и fplot или polar (в полярной системе координат).
Функция plot имеет различные формы, связанные с входными параметрами, например p lot (у) создает кусочно-линейный график зависимости элементов у от их индексов. Если задать два вектора в качестве аргументов, то plot(x,y) создаст график зависимости у от х.
Например, для построения графика значений функции sin от нуля до 2p сделаем следующее:
t = 0:pi/100:2*pi;
у = sin(t);
plot ( t , y ).
Вызов функции plot с многочисленными парами х-у создаст многочисленные графики. Matlab автоматически присваивает каждому графику свой цвет (исключая случаи, когда это делает пользователь), что позволяет различать заданные наборы данных. Например, следующие три строки отображают график близких функций, и каждой кривой соответствует свой цвет:
у 2 = sin(t-.25) ;
уЗ = sin(t-.5) ;
plot ( t, y, t, y2, t, уЗ).
Графики в полярной системе строятся аналогично:
t=0:0.01:2*pi;
y=3*(1+sin(t));
polar(t,y)
Для совмещения графиков в одной системе координат можно использовать функцию hold on:
t=0:0.01:2*pi;
y1=3*(1 + sin(t));
y2=3*(1 - sin(t));
y3=3*(1 + cos(t));
y4=3*(1 - cos(t));
polar(t,y1),hold on, polar(t,y2,’r’),polar(t,y3,’g’), polar(t,y4,’k’).
Установка цветов графиков производится введением символа-обозначения цвета в число параметров функции. Обозначения цветов графиков приведены в табл. 7
Таблица 7
Обозначения цветов графиков
| Цвет | Обозначение цвета | |
| по-английски | по-русски | |
| yellow | желтый | Y |
| magenta | светло-фиолетовый | M |
| cyan | светло-зеленый | C |
| red | красный | R |
| green | зеленый | G |
| blue | голубой | B |
| white | белый | W |
| black | черный | K |
Аналогично производится выбор символов для изображения графиков из таблицы 8
Таблица 8
Символы для изображения графиков
| Символ | Обозначение символа | |
| по-английски | по-русски | |
| point | точка | . |
| circle | окружность | O |
| x-mark | крестик | X |
| star | звездочка | * |
| suare | квадратик | S |
| diamond | алмаз | D |
| triangle(down) | треугольник(углом вниз) | V |
| triangle(up) | треугольник(углом вверх) | ^ |
| triangle(left) | треугольник(углом влево) | < |
| triangle(right) | треугольник(углом вправо) | > |
| pentagram | 5-угольная звездочка | P |
| hexagram | 6-угольная звездочка | H |
| solid | непрерывная линия | - |
| dotted | пунктирная линия | : |
| dashdot | штрих-пунктирная линия | -. |
| dashed | разрывная линия | -- |
Функция hist – построение графика гистограммы заданного вектора. Стандартное обращение имеет вид: hist ( y , x ), где y – вектор, гистограмму которого нужно построить; x – вектор, определяющий интервалы изменения первого вектора, внутри которых подсчитывается число элементов вектораy.
Действия с графическими окнами. Команды работы с графическим окном находятся в главном меню окна и во всплывающем меню (щелчок правой кнопкой мыши в координатной плоскости, рис. 6).
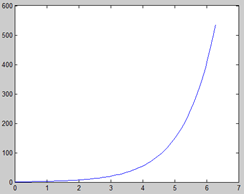
Рис. 6. Основное меню графического окна
С его помощью могут быть выполнены различные действия с графическими окнами:
– нанесение координатной сетки (пункт всплывающего меню Grid, рис. 7);
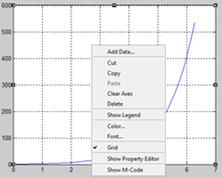
Рис. 7. Нанесение координатной сетки
– вывод информации об отдельных точках графика (наведение курсора мыши на данную точку и нажатие левой кнопки (не отпуская)); например, для временного графика будет выведена информация о текущем значении сигнала и о текущем времени (рис. 8).
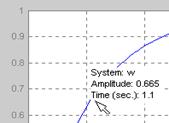
Рис. 8. Информация о координатах точки графика
Информационная надпись не исчезает при отпускании кнопки мыши. Для ее удаления необходимо щелкнуть левой кнопкой мыши на свободном поле либо правой кнопкой мыши вызвать всплывающее меню, показанное на рис. 9 и воспользоваться пунктом Delete. Аналогично выводится информационная надпись о текущем значении и текущей частоте для частотных характеристик.
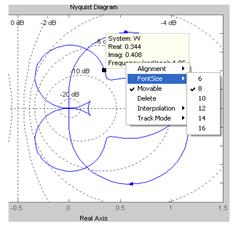
Рис. 9. Всплывающее меню при работе с графиком
Масштабирование и удаление графиков. Существует несколько способов изменения масштаба графика (как временной, так и частотной характеристики).
Первый способ – использование подменю Zoom всплывающего меню (см. рис. 6). Пунктами подменю Zoom являются:
In - X – масштабирование по горизонтали;
In - Y – масштабирование по вертикали;
X - Y – масштабирование по вертикали и по горизонтали (выделение прямоугольного фрагмента);
Out – возврат исходного масштаба.
Масштабирование выполняется мышью, при удержании нажатой левой кнопки, путем проведения горизонтальной линии (In - X), вертикальной линии (In - Y) или прямоугольника (X - Y).
Второй способ изменения масштаба – использование окна параметров координатной плоскости. Для вывода окна параметров необходимо сначала войти в режим редактирования графического окна, нажав мышью кнопку с изображением стрелки в меню окна, а затем выполнить двойной щелчок по координатной плоскости (но не по самому графику!). В результате появится окно параметров (рис. 10).
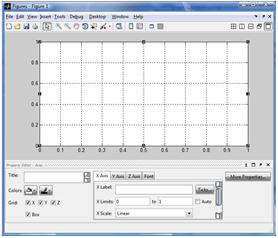
Рис. 10. Окно параметров графического окна
Максимальное и минимальное значения по оси X и оси Y (для разных характеристик эти оси имеют разный смысл) задаются в строках ввода напротив надписи Limits. При этом должен быть установлен флажок ручного ввода пределов Manual.
Иногда требуется скрыть некоторые графики (если на одной координатной плоскости их несколько). Для того чтобы скрыть графики (с возможностью последующего восстановления) используется всплывающее меню графического окна (режим редактирования выключен). В подменю Systems перечислены имена всех объектов, характеристики которых были выведены в окно. Для того чтобы скрыть график, необходимо снять флажок напротив имени объекта.
Изменение параметров графиков. Для изменения параметров графика можно использовать всплывающее меню графика (рис. 10). Для его вывода необходимо в режиме редактирования графического о кна выполнить щелчок правой кнопкой мыши при наведении курсора на сам график.
Для изменения толщины линии используется подменю Line Width, для изменения стиля линии (сплошная, пунктирная и т.д.) – подменю Line Style. При выборе пункта Color … появляется окно установки цвета линии. Те же действия можно выполнить, используя окно установки параметров графика (пункт Properties …).
Оформление графического окна. Для добавления текстовых комментариев нажмите мышью кнопку Insert – TextBox меню графического окна. Затем выполните щелчок мыши в нужном месте координатной плоскости, введите текст и выполните щелчок мыши в любом другом месте координатной плоскости. В режиме редактирования графического окна можно перетаскивать текстовую надпись с помощью мыши на любое место координатной плоскости.
Для введения заголовка над координатной плоскостью заполните строку Title в окне параметров Insert. Для введения поясняющих надписей для осей – строки Label для оси X и для оси Y.
Сохранение графического окна. Для сохранения координатной плоскости и ее содержимого в графическом файле используется пункт Export … в подменю File … главного меню графического окна. В окне сохранения файла задается тип файла (например, Bitmapfiles *. bmp) и имя файла. Файлы типа Bitmap могут быть открыты графическим редактором Paint.
Ввод и действия с комплексными числами. Язык системы M atlab, в отличие от многих языков программирования высокого уровня, содержит очень простую в пользовании встроенную арифметику комплексных чисел Большинство элементарных математических функций построено таким образом, что аргументы предполагаются комплексными числами, а результаты также формируются как комплексные числа. Эта особенность языка, делает его очень полезным для инженеров и научных работников.
Для обозначения мнимой единицы в M atlab зарезервировано два имени - i и j. Ввод с клавиатуры значения комплексного числа производится путем записи в командном окне строки вида:
<Имя переменной> = <Значение ДЧ> + i*<Значение МЧ>,
где ДЧ - действительная часть комплексной величины;
МЧ - мнимая ее часть.
Пример ввода комплексного числа:
I=34.63-j*13.965
I =
34.63 - 13.965i
Простейшие действия с комплексными числами - сложение, вычитание, умножение, деление и возведение в степень - осуществляются с помощью обычных арифметических знаков +, -, *, /, \ и ^ соответственно. Далее, в разделе расчетов цепей переменного тока мы покажем, как это выглядит на примерах.
Практически все элементарные математические функции, переченькоторых приведен далее, вычисляются при комплексном значении аргумента и получают в результате этого комплексные значения результата.
Благодаря этому, например, функция sqrt (корень квадратный), в отличие от других языков программирования, вычисляет квадратный корень из отрицательного аргумента, а функция abs (абсолютное значение) при комплексном значении аргумента вычисляет модуль комплексного числа.
» x=sqrt(5-j*4)
x =
2.3878 - 0.83759i
» y=abs(x)
y =
2.5304
В M atlab есть несколько дополнительных функций, рассчитанныхтолько на комплексный аргумент:
real(Z) - выделяет действительную часть комплексного аргумента Z;
imag(Z) - выделяет мнимую часть комплексного аргумента;
angle(Z) - вычисляет значение аргумента комплексного числа Z (врадианах от -π до +π);
conj(Z) - выдает число, комплексно сопряженное относительно Z.
Кроме того, в M atlab есть специальная функция cplxpair(V), которая осуществляет сортировку заданного вектора V с комплексными элементами таким образом, что комплексно-сопряженные пары этих элементов располагаются в выходном векторе в порядке возрастания их действительных частей, при этом элемент с отрицательной мнимой частью всегдарасполагается первым. Действительные элементы завершают комплексно-сопряженные пары.
Приспособленность большинства функций M atlab к оперированию с комплексными числами позволяет значительно проще строить вычисления с действительными числами, результат которых является комплексным (например, находить комплексные корни квадратных уравнений).
Решение систем линейных уравнений в среде MatLab . Система MatLab имеет библиотеку для реализации задач линейной алгебры. В ее составе можно выделить, в частности, следующие функции и операции.
D=det(A) - определитель (для квадратной матрицы);
R=rank(A) - ранг матрицы (число линейно независимых строк / cтолбцов);
T=norm(A) - норма матрицы ||A||2;
О=inv(A) - обращение матрицы (при близости матрицы к вырожденной выдаются предупреждения о ненадежности результатов); часто используется для решения системы АХ=В в форме:
Х= inv(A) *В;
X=B/A , X=A\B - решение системы АХ=В (B –матрица правой части):
» A=[1 2; 3 1]
A=12
31
» B=[5;5]
B=5
5
» X=A\B
X=1
2
» X=B'/A'
X = 1 2
» B=[5 13;5 17]
B=5 13
5 17
» X=A\B
X=1.0 4.20
2.0 4.40
Интегрирование системы обыкновенных дифференциальных уравнений осуществляется при помощи функций ode 23 и ode 45. Функция ode 23 осуществляет интегрирование численным методом Рунге-Кутта 2-го порядка, а с помощью метода 3-го порядка контролирует относительные и абсолютные ошибки интегрирования на каждом шаге и изменяет величину шага интегрирования так, чтобы обеспечить заданные пределы ошибок интегрирования. При использовании функции ode 45 интегрирование осуществляется методом Рунге-Кутта 4-го порядка, а величина шага контролируется методом 5-го порядка.
Система дифференциальных уравнений должна быть представлена в форме Коши:
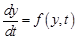 ,
,
где y – вектор переменных состояния системы, t – аргумент (обычно время), f – нелинейная вектор-функция от переменных состояния у и аргумента t.
Обращение к процедурам численного интегрирования имеет вид
[t, y] = ode23(‘< имя функции >’, tspan, y0, options)
[t, y] = ode45(‘< имя функции >’, tspan, y0, options),
где <имя функции> – имя m-файла, являющегося функцией Matlab от t и y , в котором вычисляется вектор функция f(y , t), т.е. правые части системы дифференциаль-ных уравнений; tspan – вектор задающий интервал интегрирования [t0 tfinal], t0 – начальное значение интервала, tfinal – конечное; y0 – вектор начальных условий; options – строка параметров, определяющих значения допустимой относительной и абсолютной погрешности интегрирования. Этот параметр можно не указывать, если пользователя устраивают значения погрешностей, заданных по умолчанию, т.е. относительная погрешность интегриро-вания 1.0e-3,а абсолютная (по каждой из переменных состояния) – 1.0e-6. В противном случае, перед обращением к процедуре ode 23 следует указать значения погрешностей при помощи процедуры odeset.
Результатом интегрирования является матрица проинтегрированных значений фазовых переменных y, в которой каждый столбец соответствует одной из переменных состояния, а строка содержит значения переменных состояния, соответствующих определенному шагу интегрирования, т.е. значению вектора t.
Пусть задана система обыкновенных дифференциальных уравнений:
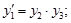
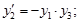
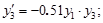
с начальными условиями: 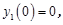
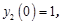
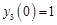 .
.
Для интегрирования данной системы уравнений необходимо создать m-файл, который является функцией переменных t и y. Для создания файла воспользуемся редактором Matlab Editor / Debugger, который вызывается из основного меню File – New – Blank M-File. Текст файла:
function
dy=rigid(t,y)
dy=zeros(3,1);
dy(1)=y(2)*y(3);
dy (2)=- y (1)* y (3);
dy (3)=-0.51* y (1)* y (2);
Название файла и функции должны совпадать. Файл надо сохранить с названием rigid.
В этом примере абсолютная и относительная погрешность задается при помощи команды odeset, время интегрирования зададим в интервале от 0 до 12 [0 12], вектор начальных условий [0 1 1]. Для осуществления процедуры интегрирования в рабочем пространстве Matlab необходимо набрать:
» options=odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-5]);
» [t,y]=ode45('rigid',[0 12],[0 1 1],options);
Чтобы просмотреть результаты в рабочем пространстве Matlab необходимо ввести в командной строке y. Графически результаты выводятся при помощи команды plot
» plot(t,y(:,1),'-',t,y(:,2),'-.',t,y(:,3),'.').
с постоянными параметрами. Объект может являться моделью всей системы, ее части или отдельного элемента системы.
Нахождение корней полиномов. Система Matlab имеет функцию roots ( P ), которая вычисляет вектор, элементы которого являются корнями заданного полинома Р.
Рассмотрим пример. Пусть задан полином:
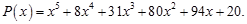
В системе Matlab полином задается вектором его коэффициентов:
>> p=[1,8,31,80,94,20].
При вводе функции roots ( p ) вычисляются корни полинома p:
>> roots ( p ).
Ввод моделей в виде пространства состояний производится по заданным матрицам A, B, C, D уравнений состояния системы:
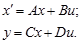
Матрицы вводятся в рабочем пространстве Matlab в квадратных скобках по срокам через точку с запятой. Например, матрица
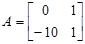
вводится следующим образом:
>> A=[0 1;−10 1].
Модель в виде пространства состояний вводится при помощи функции
sys = ss ( A , B , C , D ),
где sys – произвольное название системы. Перед вводом этой команды необходимо ввести в рабочее пространство Matlab последовательно матрицы A,B,C,D.
Построение основных характеристик объекта. Создав объект с определенной структурой и параметрами, можно исследовать различные характеристики объекта. Графики характеристик строятся в специальных графических окнах. Рассмотрим способы получения основных временных и частотных характеристик (табл.9 – 12).
Примечание 1. Обозначение координатных осей графического окна производится при выводе временных характеристик:
Amplitude – ось значений выходной величины объекта;
Time ( sec ) – ось времени (единицы – секунды).
Таблица 9
Исследование переходной функции и весовой функции
| Команда | Комментарий |
| step(w) impulse(w) | Построение переходной функции (step) и весовой функции (impulse) функции объекта w. Время моделирования определяется автоматически |
| step(w,t) impulse(w,t) | Построение переходной (весовой) функции объекта wна заданном отрезке времени от 0 до t (где t – это константа или переменная); t также можно задавать как массив вида 0: dt : tmax, где tmax – время окончания моделирования, dt – шаг расчета переходной функции (должен быть достаточно малым) |
| step(w1,w2,…,wn) impulse(w1,w2, …,wn) | Построение переходной (весовой) функции нескольких объектов на одной координатной плоскости |
| step(w1,w2,…,wn,t) impulse(w1,w2, …,wn,t) | То же с заданием времени моделирования |
Таблица 10
Исследование реакции на произвольно заданное воздействие
| Команда | Комментарий |
| lsim(w,u,t) | Построение реакции объекта w на воздействие заданное двумя массивами. Массив t – это массив значений времени. Задается в виде 0: dt : tmax, где tmax – время окончания моделирования, dt – шаг расчета (должен быть достаточно малым). Массив u – это массив значений входного воздействия того же размера, что и массив t |
| lsim(w1,w2,…,wn,u, t) | То же для нескольких объектов (графики выводятся на одну координатную плоскость) |
Таблица 11
Исследование АФЧХ – амплитудно-фазовой частотной характеристики (Nyquistdiagram)
| Команда | Комментарий |
| nyquist(w) | Построение АФЧХ объекта w |
| nyquist(w,{omin,omax}) | То же с заданием диапазона частот, для которого строится АФЧХ (в фигурных скобках). Частота ominдолжна быть больше нуля |
| nyquist(w1,w2,…,wn) | Построение АФЧХ нескольких объектов на одной комплексной плоскости. |
| nyquist(w1, …,wn,{omin, omax}) | То же с заданием диапазона частот |
Примечание 2. Амплитудно-фазовая частотная характеристика строится в виде годографа на комплексной плоскости для диапазона частот –∞…∞ и представляет собой две симметричные относительно действительной оси кривые: одна для положительных частот, другая для отрицательных частот. В отечественной литературе принято строить амплитудно-фазовую частотную характеристику строить только для положительных частот. Обозначение осей комплексной плоскости в графическом окне: RealAxis– действительная ось, ImaginaryAxis – мнимая ось.
Таблица 12
Исследование ЛЧХ – логарифмических частотных характеристик
(Bodediagram)
| Команда | Комментарий |
| bode(w) | Построение ЛЧХ объекта w |
| bode(w,{omin, omax}) | То же с заданием диапазона частот Частота omin должна быть больше нуля |
| bode(w1,w2,…,wn) | Построение ЛЧХ нескольких объектов в одном окне |
| bode(w1,w2,…,wn,{omin, omax}) | То же с заданием диапазона частот |
| margin(w) | Построение ЛЧХ объекта w с выводом информации о запасах устойчивости автоматической системы по амплитуде и по фазе. Объект w должен описывать разомкнутую систему |
Примечание 3. Команды bode и margin всегда строят 2 логарифмические частотные характеристики в одном окне друг под другом в одном масштабе частоты: ЛАЧХ – логарифмическую амплитудную частотную характеристику и ЛФЧХ – логарифмическую фазовую частотную характеристику. Обозначение координатных осей: Magnitude(dB) – ось значений амплитудно-фазовой частотной характеристики в децибелах, Phase(deg) – ось значений логарифмической фазовой частотной характеристики в градусах, Frequency(rad / sec) – ось частоты (в радианах в секунду).
Для того чтобы построить новую характеристику в другом графическом окне (при сохранении на экране уже имеющегося графического окна) необходимо ввести команду figure (создается новое пустое графическое окно); после запуска следующей команды вывода графиков они появятся в новом окне. При построении нескольких характеристик на одной координатной плоскости каждый график строится своим цветом в зависимости от порядка построения. Стандартным для Matlab является следующий порядок цветов графиков: синий, зеленый, красный, голубой, фиолетовый.
Построение амплитудно-фазовой характеристики W(jw) в командном окне Matlab. Набор исходных данных, функции W и графической команды plot представлен ниже:
>> k=12;
z=0.1;
T=1;
w=0:0.01:100;
W=k./(T.^2.*(w.*j).^2+2.*T.*z.*w.*j+1);
plot(real(W), imag(W))
Далее с помощью пункта меню Insert → XLabel → LabelY → Title окна Figure № вводятся обозначения осей и заголовок рисунка. Общий вид изображения амплитудно-фазовой характеристики показан на рис. 18.
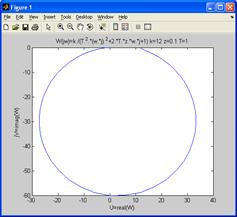
Рис. 18. Изображение амплитудно-фазовой характеристики
Щелкнув правой кнопкой мыши на поле рисунка, можно вызвать всплывающее меню, с помощью которого вводится координатная сетка (пункт Grid). С помощью пункта меню View → Plot Browser можно изменить тип, форму и цвет линий графика.
Построение расчетных логарифмических амплитудной LР (w) и фазовой arР(w) частотных характеристик производится в соответствии со следующими ниже правилами.
1. Характеристики строятся в полулогарифмических координатах (ось Х – логарифмическая, ось У – естественная) с использованием функции semilogx, у которой правила ввода аргументов и значений спецификатора кривой аналогичны функции plot.
2. В силу особенностей функции Matlab atan(x) = arctg(x) (выдаются значения только в диапазоне от -π/2 до π/2), функция ar(w) набирается в виде двух выражений (см. текст последовательности вычислений ниже).
3. Каждая характеристика набирается отдельным графиком, и ввод заканчивается командой holdon, обеспечивающей вывод последующего графика в то же текущее окно рисунка.
4. Из набранных осевых надписей Matlab выводит только последние (ar2 и log(w2)).
Для вывода всех необходимых надписей следует:
– в окне Figure No.1 командой меню Edit – AxesProperties вызвать окно редактора заголовка и осевых надписей (Property Editor) и ввести необходимые тексты; кнопки Editрядом с каждым оконцем позволяют менять у текста тип шрифта и его параметры;
– нажатием кнопки «А» и щелчком левой кнопки мышки ввести текстовое поле (с последующим вводом текста) для пометки выбранной кривой (стрелка вставляется нажатие кнопки «Стрелка» с последующим вычерчиванием линии левой кнопкой мышки).
Характеристики набираются в командном окне согласно формул (10) и (11) в соответствии с цепочкой команд:
>> k=12;
z=0.1;
T=1;
w=0:0.01:100;
W=k./(T.^2.*(w.*j).^2+2.*T.*z.*w.*j+1);
L=20.*log10(k./sqrt((2.*T.*z.*w).^2+(1-T.^2.*w.^2).^2));
semilogx(w,L);
hold on;
w1=0.1:0.01:1;
ar1=-(180./pi).*atan(2.*T.*z.*w1./(1-T.^2.*w1.^2));
semilogx(w1,ar1);
hold on;
w2=1.01:0.01:100;
ar2=-180-(180./pi).*atan(2.*T.*z.*w2./(1-T.^2.*w2.^2));
semilogx(w2,ar2);
Warning: Divide by zero.
(Type "warning off MATLAB:divideByZero" to suppress this warning.).
После нажатия клавиши Enter , завершающего ввод команд, Matlab построит графики на поле рисунка FigureNo .1 (рис.19), причем надписи на рисунке дополнительно редактируются средствами окна рисунка Figure No .1.
Последние две строки – это сообщение Matlab, которое игнорируется.
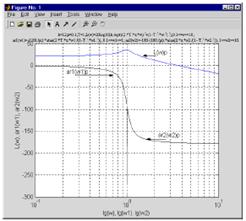
Рис.19. Логарифмические амплитудная и фазовая частотные характеристики звена
1.3. Работа с приложением Simulink
Модели элементов. После запуска Matlab запуск Simulink может быть произведен с использованием соответствующего раздела меню Start пакета Matlab (рис. 20).
При этом происходит переход к обозревателю библиотеки модулей Simulink Library Browser, из которой вызываются модели компонентов исследуемой системы, показанные на рис. 21.
В настоящей работе мы будем пользоваться частью библиотеки Simulink, включающей в себя разделы:
– Continuous – модели линейных непрерывных систем;
– Math Operations – модели математических операций;
– Sinks – приемники сигналов;
– Sourses – источники сигналов;
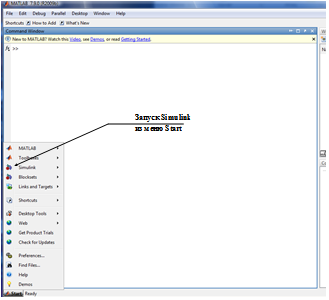
Рис. 20. Средства запуска Simulink
Приложение SimPowerSystem, непосредственно используемое для решения задач электротехники, рассматривается в следующих лабораторных работах.
Библиотека блоков. Внешний вид наиболее часто встречающихся в системах управления элементов показан на рис. 22.
Рассмотрим некоторые блоки, входящие в состав библиотеки. Каждый блок имеет определенное число входов и выходов для связи с другими блоками модели. Некоторые блоки имеют только входы или только выходы. Свойства блоков определяются параметрами, задаваемыми пользователем. Эти параметры вводятся в окне параметров, для раскрытия которого выполняется двойной щелчок левой кнопкой мыши по изображению блока.
Первые четыре блока (рис.22, а–г, библиотека Sourses)
представляют собой настраиваемые источники сигнала. Они имеют один выход и не имеют входов.
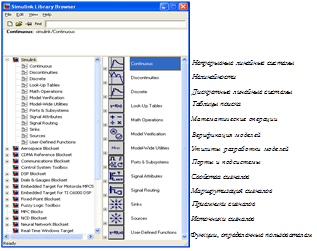
Рис. 21. Окно библиотеки модулей Simulink

а б в г

д е ж з
и к
Рис. 22. Блоки-компоненты систем управления
Источник постоянного сигнала (константа), рис.22, а, формирует постоянный сигнал заданной величины.
Параметр блока: ConstantValue – значение константы.
Источник ступенчатого сигнала (Step), рис.22,б, формирует ступенчатый сигнал (рис. 23).
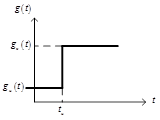
Рис. 23. Ступенчатый сигнал
Параметры блока:
Steptime – время скачка сигнала.
Initialvalue – начальное значение.
Finalvalue – конечное значение.
Источник линейно изменяющегося сигнала (Ramp), рис. 22,в, формирует сигнал, возрастающий или убывающий с постоянной скоростью (рис. 24).

Рис. 24. Линейно возрастающий сигнал
Параметры блока:
Slope – наклон (значение производной по времени).
Starttime – время начала действия сигнала.
Источник синусоидального сигнала, рис. 22,г, формирует сину-соидальный сигнал с заданной частотой, амплитудой и начальной фазой.
Параметры блока:
Amplitude – амплитуда.
Frequency ( rad / sec ) – частота в рад/с.
Phase ( rad ) – начальная фаза в радианах.
Графический индикатор сигналов, рис.22,д, предназначен для наблюдения результатов моделирования – временных графиков величин модели. Блок имеет один вход, куда подается исследуемый сигнал модели, и не имеет выходов. В модели можно использовать только один индикатор. Наблюдение нескольких графиков в одном окне осуществляется с помощью мультиплексора. После того как расчет модели произведен компьютером, можно посмотреть результат, для чего необходимо выполнить двойной щелчок по значку индикатора. В результате раскрывается графическое окно с графиком сигнала в функции времени.
Мультиплексор, рис.22,е, имеет несколько входов, число ко-торых определяется пользователем, и один выход. Мультиплексор объединяет несколько сигналов в один векторный сигнал, который передается в модели по одной линии. Использование мультиплексора позволяет подать на индикатор несколько сигналов и наблюдать их графики на одной координатной плоскости.
Параметр блока: Number of inputs – число входов.
Остальные блоки (рис. 22,ж – к) представляют собой преобразователи сигналов.
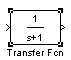
Линейное динамическое звено, рис. 22, ж.
Параметры блока:
Numerator – массив коэффициентов числителя передаточной функции.
Denominator – массив коэффициентов знаменателя передаточной функции.
Коэффициенты числителя и знаменателя передаточной функции задаются по тем же правилам, как в Control System Toolbox. После ввода параметров передаточная функция показывается внутри значка блока.
Пропорциональное звено, рис. 22, з, умножает сигнал на величину Gain.
Параметр блока: Gain – коэффициент передачи.
Звено запаздывания, рис. 22, и, выполняет задержку сигнала на выходе блока относительно входного сигнала, при этом полностью сохраняет форму входного сигнала.
Параметр блока: Time delay – время задержки.
Сумматор, рис. 22, к, выполняет алгебраическое суммирование (сложение или вычитание) заданного числа входных сигналов. Графическая форма сумматора может быть изменена после вывода элемента в окно модели (щелчок на сумматоре левой кнопкой мыши →Sum parameters во всплывающем окне →Icon Shape).
Параметр блока: List of signs – список знаков. В список знаков записываются плюсы и минусы без пробелов (например +–++). Тем самым определяется число входов сумматора, и знак каждого слагаемого.
Действия с блоками. В состав основных действий с блоками входят:
– вставка блока из библиотеки в окно модели;
– выделение блока;
– удаление блока;
– изменение размеров блока;
– изменение атрибутов блока;
– копирование блока;
– изменение ориентации блока.
Вставка блока из окна библиотеки в окно модели выполняется с помощью мыши (удерживая левую кнопку). При этом окно модели должно быть предварительно создано (File → New → Model).
Выделение блоков. Блок может быть выделенным или невыделенным. Для выделения блока выполняется однократный щелчок левой кнопкой мыши по значку блока. Выделение показывается четырьмя квадратными метками по углам значка блока (рис. 25, а). Для выделения нескольких блоков выполняется однократный щелчок мышью по значкам блоков с удержанием клавиши Shift или путем обведения прямоугольного участка окна рамкой.
Удаление блоков. Нажатие клавиши Delete приводит к удалению всех выделенных блоков.
а б в
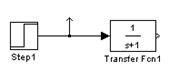
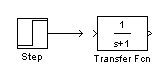
Соединение выполнено Соединение не выполнено
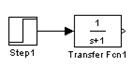
г д
Рис. 25. Действия с блоками
Изменение размеров блока. Значок блока можно растягивать, захватив мышью за квадратные угловые метки.
Изменение имени блока. Чтобы ввести новое имя блока выполняется однократный щелчок левой кнопкой мыши по старому имени. Имя блока обводится рамкой и появляется курсор (рис. 25,б). После этого можно редактировать имя. Не допускается отсутствие имени блока (пустая строка) и наличие в одном окне блоков с одинаковыми именами.
Вращение блока. При выполнении щелчка правой кнопкой мыши по значку блока появляется всплывающее меню блока, где находится подменю Format. В подменю Format содержатся команды: Rotate block – вращение блока на 90° по часовой стрелке, Flip block – разворот блока на 180°, Flip name – переброска имени на другую сторону блока.
Создание копии блока. Для создания копии необходимо захватить блок, удерживая правую кнопку мыши и перетащить на свободное место окна.
Сборка схемы модели. Сборка модели включает в себя выполнение следующих действий:
– компоновка блоков;
– проведение и корректировка соединительных линий;
Компоновка блоков состоит в таком их размещении на экране, при котором структура соединительных линий будет выглядеть наиболее просто.
Проведение соединительных линий. Для соединения выхода одного блока с входом другого указатель мыши наводится на исходную точку и затем проводится линия (удерживая левую кнопку мыши). Когда линия доведена до конечной точки, кнопка мыши отпускается. Жирный конец стрелки означает, что соединение выполнено (рис.25, г). Если линия осталась не подключенной, конец стрелки будет тонким (рис.25, д). Неподключенную стрелку затем можно продолжить. Линии можно захватывать мышью и изменять их конфигурацию.
Отделение блока от линии. Для отделения блока он захватывается мышью с удержанием клавиши Shift и перетаскивается на другое место.
Удаление линий. Линии, как и сами блоки, можно выделять. После нажатия клавиши Delete выделенные линии удаляются.
Создание узлов. Для создания узла на линии новая линия тянется от выбранной точки с удержанием правой кнопки мыши (рис.10, в).
Чтобы собрать схему, сначала необходимо выполнить следующие действия:
1. "Перетащить" все нужные звенья из соответствующих наборов на пространство модели untitled, предназначенное для составления блок-схемы вашей модели. Делается это следующим образом: выбрать элемент в библиотеке, нажать на элементе левой кнопкой мыши и, не отпуская кнопку, перенести указатель мыши в окно построения модели и там отпустить.
В соответствии со схемой на рис. 4 нам необходимы: источник скачкообразного возмущения для 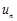 , сумматор, три усилителя, два интегратора, два источника постоянного сигнала (для задания начальных условий) и осциллограф. После выбора на структурной схеме модели будут помещены все необходимые элементы, рис. 26.
, сумматор, три усилителя, два интегратора, два источника постоянного сигнала (для задания начальных условий) и осциллограф. После выбора на структурной схеме модели будут помещены все необходимые элементы, рис. 26.
2. Связать между собой эти звенья, соединив их в соответствии со схемой, рис. 4. Для этого вначале необходимо разместить звенья так, чтобы было удобно проводить соединения. Затем нужно установить курсор на выходе нужного звена и нажать левую кнопку мыши. При этом указатель примет вид перекрестия. Теперь, не отпуская кнопки, "тащить" появившуюся линию до входа другого звена. Когда указатель примет вид двойного перекрестия, отпустить кнопку. Система создаст связь между элементами и обозначит ее стрелкой по направлению сигнала.
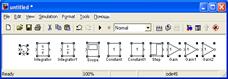
Рис. 26. Пространство модели с размещенными в нем звеньями будущей модели
Другие действия по размещению элементов и построению соединительных линий приведены ниже:
– если подвести линию от входа элемента к другой, уже существующей, линии связи и отпустить кнопку мыши, то система создаст узел, в котором сигнал расходится в двух направлениях;
– если необходимо перевернуть звено, то его сначала выделить одинарным щелчком мыши (появятся точки по углам элемента). Затем, нажимая Ctrl+R, добиться нужного расположения.
– линии связи, как и элементы, удаляют выделением и нажатием Del; выделенная связь обозначается двумя пустыми точками на ее концах.
Перемещение целой группы элементов "с вытягиванием линий связи" осуществляется в два этапа. Сначала выделяем прямоугольную область, которая охватывает нужные вам элементы. При этом все элементы этой области будут "помечены". Затем, "ухватив" любой отмеченный элемент из этой области, перемещаем его в нужное место и отпускаем. В результате переместятся все элементы отмеченной области.
3. Для установки нужного количества входов сумматора (в нашем примере – три) поступают следующим образом. Двойным щелчком на сумматоре открывают меню его свойств. В строке этого меню задают последовательность плюсов и минусов, которая определит количество входов и знаки, считая сверху вниз, с которыми сигналы будут суммироваться. В нашем примере возмущающее воздействие суммируется с положительным знаком, а нулевая и первая производные ̶ с отрицательными (комбинация " + - - ").
4. Чтобы иметь возможность задавать начальные условия от внешнего источника, в свойствах интеграторов, в меню Источник исходных условий (Initial condition source) выбирают внешний (external). После этого на иконке интегратора появляется еще один вход (нижний), на который и подают сигнал задания начального условия. В нашем примере это будет источник постоянного сигнала. Меню свойств закрывают нажатием кнопки ОК.
5. Величину постоянного сигнала задают в свойствах источника (строка Constant value). Величину коэффициента усиления задают в свойствах усилителя (строка Gain) как показано на рис. 27.
Величину и время скачкообразного возмущения задают в свойствах источника скачкообразного возмущения. Там же определяют момент поступления возмущения (строка Steptime), значения сигнала до и после возмущения (строки Initial value и Fina lvalue соответственно).
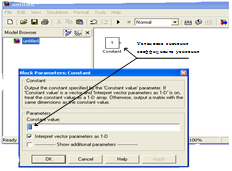
Рис. 27. Пример установки параметров источника сигнала
6. Окончательный вид готовой блок-схемы модели показан на рис. 28.
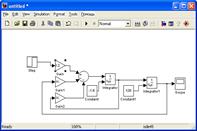
Рис. 28. Модель системы в рабочем окне Simulink
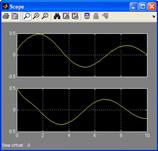
7. Запуск модели в работу, т.е. начало собственно процесса моделирования производится нажатием кнопки  или через команду Start меню Simulation. Двойной щелчок на иконке осциллографа (Scope) открывает его окно, в котором можно наблюдать изменение выходных переменных во времени, как показано на рис. 29.
или через команду Start меню Simulation. Двойной щелчок на иконке осциллографа (Scope) открывает его окно, в котором можно наблюдать изменение выходных переменных во времени, как показано на рис. 29.
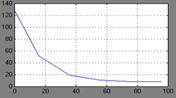
Рис. 29. Изображение выходного сигнала на экране осциллографа
Для удобства наблюдения рекомендуется разбить весь экран монитора по горизонтали на два поля: в верхнем поле развернуть осциллограф, а в нижнем оставить модель (или наоборот, вверху блок-схема модели, а внизу экран осциллографа).
8. Настройка длительности процесса моделирования производится в меню Simulation окна построения модели untitled (Simulation→Simulation parameters). В этом меню в закладке Solver (Решатель) можно выставить время начала процесса моделирования (поле Starttime) и его конца (поле Stoptime).
9. Настройка параметров осциллографа осуществляется следующим образом. При двойном щелчке левой кнопкой мыши на иконке осциллографа появляется его экран с координатной разметкой. При нажатии на вторую справа кнопку (Параметры) на панели инструментов появляется окно с двумя закладками Axes и Settings. Используя закладку Axes, устанавливаем размеры по вертикали (Ymin, Ymax). Кнопкой "бинокль"  на панели инструментов осциллографа можно автоматически подобрать степень увеличения, при которой на осциллографе видны все участки уже полученных кривых без "зашкаливания". Сохранить эти настройки осциллографа можно кнопкой
на панели инструментов осциллографа можно автоматически подобрать степень увеличения, при которой на осциллографе видны все участки уже полученных кривых без "зашкаливания". Сохранить эти настройки осциллографа можно кнопкой  , расположенной там же, справа от "бинокля". Действие "увеличительных стекол" X и Y надо испробовать самим. Они предназначены для разворачивания на весь экран какой-либо интересующей части графиков. Разметка оси абсцисс (времени) устанавливается автоматически в соответствии с величинами StartTime и StopTime, (если употребить слово auto в поле Timerange).
, расположенной там же, справа от "бинокля". Действие "увеличительных стекол" X и Y надо испробовать самим. Они предназначены для разворачивания на весь экран какой-либо интересующей части графиков. Разметка оси абсцисс (времени) устанавливается автоматически в соответствии с величинами StartTime и StopTime, (если употребить слово auto в поле Timerange).
10. Работу модели можно приостановить кнопкой Pause, в которую превращается кнопка запуска моделирования (п. 9) после ее нажатия. Рядом, справа расположена кнопка возврата в начальное состояние.
11. Simulink автоматически преобразует блок-схему модели в систему дифференциальных уравнений. Выбор метода интегрирования этой системы можно произвести также через меню Simulation. На панели Solver options в меню Simulation можно выставить шаг интегрирования (левое поле) и тип решателя (правое поле). По умолчанию выставлен автоподбор шага (Variable step) и интегрирование методом Дорманда-Принца (ode5 Dormand-Prince). Там же можно выставить допустимые Абсолютную погрешность и Относительную погрешность интегрирования (поля Absolute tolerance и Relative tolerance соответственно).
12. Многолучевой осциллограф получается добавлением элемента – мультиплексора Mux из библиотеки Signal Routing, рис. 30. В этом случае можно наблюдать в одних координатах одновременно несколько сигналов, например 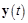 ,
, 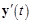 ,
, 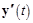 ,
, 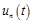 . Двойным щелчком мыши на мультиплексоре открывается меню его свойств, где можно выставить количество входов.
. Двойным щелчком мыши на мультиплексоре открывается меню его свойств, где можно выставить количество входов.
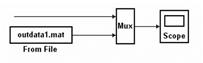
Рис. 30. Подключение мультиплексора к приемнику сигналов
13. Запись кривых – результатов моделирования (для долговременного хранения и дальнейшего использования) осуществляется подсоединением на место осциллографа (или параллельно с ним) элемента В Файл (ToFile), расположенного в наборе Приемники (Sinks), как показано на рис. 31.
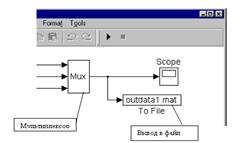
Рис. 31. Подключение мультиплексора для записи результатов моделирования в файл
В свойствах элементаВ Файл необходимо задать (придумать) имя файла c расширением "mat" (например outdata1.mat, рис. 31), в который будет производиться запись данных.
14. Сравнение вида новой(ых) кривой(ых) – результатов только что проведенного моделирования, с некоторыми "реперными кривыми", полученными ранее, легко проводить с помощью элементаИз Файла (FromFile). Для этого из набора Источники (Sources) помещаем на поле блок-схемы моделирования элементИз Файла. Это обеспечит вывод на осциллограф "реперных кривых" вместе с новой(ыми) кривой(ыми) моделирования (см. рис. 30). в свойствах элементаИз Файла необходимо указать конкретное имя файла, в котором хранятся "реперные кривые". Естественно также, что файл под этим именем ранее выступал в качестве элементаВ Файл, когда в него записывались "реперные кривые".
15. Для сохранения блок-схемы на жестком диске достаточно нажать кнопку  , расположенную на панели инструментов окна untitled. Если вы сохраняете блок-схему первый раз, вам будет предложено ввести имя, под которым будет сохранена ваша схема. При последующих сохранениях данные в файле с указанным именем будут обновляться. По умолчанию файлы сохраняются в директории "…/Matlab/ work", но настоятельно рекомендуется (чтобы не смешивались пользовательские файлы и собственные программные файлы средыMatLab) создать новую поддиректорию. Рекомендуется в качестве имени поддиректории использовать свою фамилию, записанную латинскими буквами, например "…/Matlab/Afanasiev/".
, расположенную на панели инструментов окна untitled. Если вы сохраняете блок-схему первый раз, вам будет предложено ввести имя, под которым будет сохранена ваша схема. При последующих сохранениях данные в файле с указанным именем будут обновляться. По умолчанию файлы сохраняются в директории "…/Matlab/ work", но настоятельно рекомендуется (чтобы не смешивались пользовательские файлы и собственные программные файлы средыMatLab) создать новую поддиректорию. Рекомендуется в качестве имени поддиректории использовать свою фамилию, записанную латинскими буквами, например "…/Matlab/Afanasiev/".
16. Для вызова с жесткого диска ранее сохраненной модели достаточно активизировать функцию Открытие Файла (OpenFile) кнопкой  с панели инструментов окна untitledили выбрать эту функцию из меню Файл (File). В диалоговом меню следует выбрать директорию расположения и имя ранее сохраненного файла с расширением ".mdl".
с панели инструментов окна untitledили выбрать эту функцию из меню Файл (File). В диалоговом меню следует выбрать директорию расположения и имя ранее сохраненного файла с расширением ".mdl".
17. Для того чтобы продолжить работу с моделью на другом ПК и/или в другое время, необходимо:
– сохранить Рабочее Поле (Workspace) в файл на жестком диске (mat-файлы);
– сохранить блок-схему модели в файл на жестком диске (mdl-файлы);
– сохранить на жестком диске файлы-функции (если вы их создавали в окне MatLabEditor/Debugger(m-файлы);
– переписать все файлы, созданные в трех предыдущих пунктах, на внешнее ЗУ.
Методы контроля правильности набора схем и установки коэффициентов. Первым и наиболее общим показателем правильности составления структурной схемы и установки коэффициентов является изменение всех переменных в допустимых границах. Если после нажатия кнопки Пуск некоторые переменные монотонно возрастают и "уходят в бесконечность", то схема собрана неверно. Причиной этого может быть наличие интегратора, не охваченного обратной связью (неправильно сделаны соединения), или установка большого значения коэффициента усиления в статике (неправильно установлены коэффициенты).
Если решение сильно колебательное, то это может характеризовать: отсутствие обратных связей по производным (например, при решении дифференциального уравнения второго порядка) или наличие большого коэффициента усиления.
Если переменные не выходят за предусмотренные пределы, то следующие количественные методы позволяют оценить точность моделирования.
Проверка правильности выставления коэффициентов передачи по коэффициенту усиления в статике. На вход собранной схемы подают скачкообразное возмущение. Например 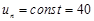 , рис. 32.
, рис. 32.
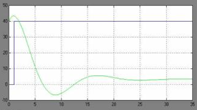
Рис. 32. Изображение входного единичного воздействия и его результатов
После окончания переходного процесса измеряют численное значение выходной величины 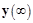 . Это удобно сделать, подсоединив параллельно осциллографу элемент Дисплей (Display) из набора Приемники (Sinks).
. Это удобно сделать, подсоединив параллельно осциллографу элемент Дисплей (Display) из набора Приемники (Sinks).
Пусть для модели, описываемой уравнением
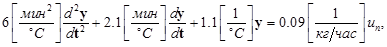
получилось 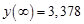 .
.
Следовательно, полученный коэффициент усиления будет
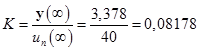 .
.
Сравниваем полученный коэффициент в статике с действительным по приведенному выше уравнению
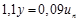 ,
, 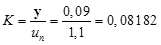 .
.
Коэффициенты усиления в статике должны совпадать с необходимой точностью. Если нужна более высокая точность, то следует вновь выставить коэффициенты, взяв большее количество знаков после десятичной точки.
Проверка правильности выставления коэффициентов по характеру переходного процесса (решения) для дифференциальных уравнений второго порядка. На вход собранной схемы подают скачкообразную возмущающую функцию, например 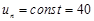 , и наблюдают характер решения (переходного процесса), см. рис. 32.
, и наблюдают характер решения (переходного процесса), см. рис. 32.
Если объект является объектом второго порядка, то, в зависимости от корней характеристического уравнения, могут быть получены следующие виды переходных процессов (рис. 33):
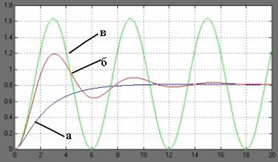
Рис. 33. Изображение входного синусоидального воздействия и его результатов
а) оба корня действительные, отрицательные – переходный процесс апериодический;
б) оба корня комплексные сопряженные – переходный процесс колебательный;
в) оба корня чисто мнимые (в уравнение не входит первая производная) – переходный процесс представляет собой незатухающие колебания.
Следовательно, для такой проверки предварительно нужно вычислить корни характеристического уравнения. Кстати, это легко за вас сделает MatLab, надо только знать соответствующие команды, которые необходимо задать в Командном Окне (MatLabCommandWindow).
Проверка правильности времени переходного процесса производится при исследовании объекта на скачкообразное возмущение: переходный процесс должен закончиться приблизительно за время, чуть большее 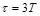 , где
, где 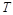 – постоянная времени при первой производной
– постоянная времени при первой производной 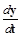 , полученная после деления всех членов дифференциального уравнения на коэффициент при
, полученная после деления всех членов дифференциального уравнения на коэффициент при 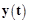 . Для уравнения
. Для уравнения
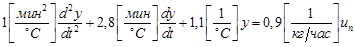 (1.16)
(1.16)
постоянная времени
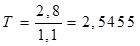 мин.
мин.
(линия «а» на рис. 33), и весь переходный процесс закончится за время
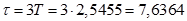 минут.
минут.
Дифференциальные уравнения и системы уравнений. Возможности использования программы Simulink не ограничиваются созданием моделей систем и наблюдением происходящих в них процессов. Рассмотрим применение этой программы для решения дифференциальных уравнений.
Дифференциальные уравнения первого порядка. Пусть необходимо решить уравнение:
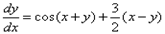
Попробуем решить его с помощью программы Simulink пакета M atlab.
Метод решения дифференциальных уравнений отличается от традиционного. Нам необходимо создать схему уравнения. Необходимо будет создать обратную связь между выходными значениями интегратора и новым значением переменной. У нашего уравнения линейно изменяется x от 0 до 20. Поэтому для решения уравнения необходимо использовать блок Ramp. В конце обязательно должен быть интегрирующий блок, а из него результат выходит на осциллограф.
Решение уравнения выглядит так:
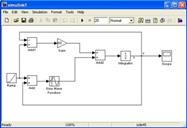
Результатом будет график x от y:
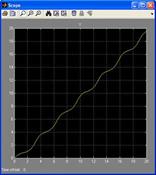
Рассмотрим из каких библиотек взяты использованные блоки.
Ramp – из Sources. Формирует линейный сигнал. В параметрах необходимо задать 1.
Add – из Math Operations. В параметрах выбираем необходимые нам операции.
Gain – из Math Operations. Коэффициент усиления сигнала. В параметрах ставим значение 3/2.
Sine Wave Function – из Sources. Т.к. нам необходим косинус, то в параметрах Phase ставим pi/2.
Integrator – из Continuous. Выполняет интегрирование входного сигнала.
Scope – из Sinks. Выводим результат – график сигнала в функции времени.
Дифференциальные уравнения 2-го порядка. Дана система уравнений:
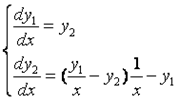
Решим ее с помощью программы Simulink пакета M atlab аналогично предыдущему случаю.
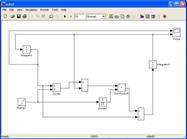
В данной системе уравнений x линейно изменяется от 1 до 10. Также необходимо сделать обратную связь между выходными значениями интеграторов и новым значение переменной x. Обязательно надо в интеграторах задать начальные значения y1(0) = 0.1; y2(0) = 0.5.
Результатом будут два графика: