Описание методов статистической обработки данных . Пример описания данных на основе полученных первичных результатов исследования
t-критерий Стьюдента – общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках. Он используется для определения статистической значимости различий средних величин. Может применяться как в случаях сравнения независимых выборок (например, группы больных сахарным диабетом и группы здоровых), так и при сравнении связанных совокупностей (например, средняя частота пульса у одних и тех же пациентов до и после приема антиаритмического препарата). В последнем случае рассчитывается парный t-критерий Стьюдента
Для применения t-критерия Стьюдента необходимо, чтобы исходные данные имели нормальное распределение. Также имеет значение равенство дисперсий (распределения) сравниваемых групп (гомоскедастичность). При неравных дисперсиях применяется t-критерий в модификации Уэлча.
При отсутствии нормального распределения сравниваемых выборок вместо t-критерия Стьюдента используются аналогичные методы непараметрической статистики, среди которых наиболее известными является U-критерий Манна — Уитни .
Для сравнения средних величин t-критерий Стьюдента рассчитывается по следующей формуле:
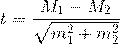
где М1 - средняя арифметическая первой сравниваемой совокупности (группы), М2 - средняя арифметическая второй сравниваемой совокупности (группы), m1 - средняя ошибка первой средней арифметической, m2 - средняя ошибка второй средней арифметической.
Полученное значение t-критерия Стьюдента необходимо правильно интерпретировать. Для этого нам необходимо знать количество исследуемых в каждой группе (n1 и n2). Находим число степеней свободы f по следующей формуле:
f = (n1 + n2) - 2
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p=0,05) и при данном числе степеней свободы f.
Если рассчитанное значение t-критерия Стьюдента равно или больше критического, найденного по таблице, делаем вывод о статистической значимости различий между сравниваемыми величинами.
Если значение рассчитанного t-критерия Стьюдента меньше табличного, значит различия сравниваемых величин статистически не значимы.
Парный t-критерий Стьюдента – одна из модификаций метода Стьюдента, используемая для определения статистической значимости различий парных (повторных) измерений.
Парный t-критерий Стьюдента используется для сравнения двух зависимых (парных) выборок. Зависимыми являются измерения, выполненные у одних и тех же пациентов, но в разное время, например, артериальное давление у больных гипертонической болезнью до и после приема антигипертензивного препарата. Нулевая гипотеза гласит об отсутствии различий между сравниваемыми выборками, альтернативная - о наличии статистически значимых различий.
Основным условием является зависимость выборок, то есть сравниваемые значения должны быть получены при повторных измерениях одного параметра у одних и тех же пациентов.
Как и в случае сравнения независимых выборок, для применения парного t-критерия необходимо, чтобы исходные данные имели нормальное распределение. При несоблюдении этого условия для сравнения выборочных средних должны использоваться методы непараметрической статистики, такие как G-критерий знаков или Т-критерий Вилкоксона.
Парный t-критерий может использоваться только при сравнении двухвыборок. Если необходимо сравнить три и более повторных измерений, следует использовать однофакторный дисперсионный анализ (ANOVA) для повторных измерений.
Парный t-критерий Стьюдента рассчитывается по следующей формуле:
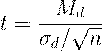
где Мd - средняя арифметическая разностей показателей, измеренных до и после, σd - среднее квадратическое отклонение разностей показателей, n - число исследуемых.
Интерпретация полученного значения парного t-критерия Стьюдента не отличается от оценки t-критерия для несвязанных совокупностей. Прежде всего, необходимо найти число степеней свободы f по следующей формуле:
f = n - 1
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p<0,05) и при данном числе степеней свободы f.
Если рассчитанное значение парного t-критерия Стьюдента равно или больше критического, найденного по таблице, делаем вывод о статистической значимости различий между сравниваемыми величинами.
Если значение рассчитанного парного t-критерия Стьюдента меньше табличного, значит различия сравниваемых величин статистически не значимы.
U-критерий Манна-Уитни – непараметрический статистический критерий, используемый для сравнения двух независимых выборок по уровню какого-либо признака, измеренного количественно. Метод основан на определении того, достаточно ли мала зона перекрещивающихся значений между двумя вариационными рядами (ранжированным рядом значений параметра в первой выборке и таким же во второй выборке). Чем меньше значение критерия, тем вероятнее, что различия между значениями параметра в выборках достоверны.
U-критерий Манна-Уитни используется для оценки различий между двумя независимыми выборками по уровню какого-либо количественного признака. U-критерий Манна-Уитни является непараметрическим критерием, поэтому, в отличие от t-критерия Стьюдента, не требует наличия нормального распределения сравниваемых совокупностей. U-критерий подходит для сравнения малых выборок: в каждой из выборок должно быть не менее 3 значений признака. Допускается, чтобы в одной выборке было 2 значения, но во второй тогда должно быть не менее пяти. Условием для применения U-критерия Манна-Уитни является отсутствие в сравниваемых группах совпадающих значений признака (все числа – разные) или очень малое число таких совпадений. Аналогом U-критерия Манна-Уитни для сравнения трех и более групп является Критерий Краскела-Уоллиса.
Сначала из обеих сравниваемых выборок составляется единый ранжированный ряд, путем расставления единиц наблюдения по степени возрастания признака и присвоения меньшему значению меньшего ранга. В случае равных значений признака у нескольких единиц каждой из них присваивается среднее арифметическое последовательных значений рангов.
Например, две единицы, занимающие в едином ранжированном ряду 2 и 3 место (ранг), имеют одинаковые значения. Следовательно, каждой из них присваивается ранг равный (3 + 2) / 2 = 2,5.
В составленном едином ранжированном ряду общее количество рангов получится равным: N = n1 + n2 где n1 - количество элементов в первой выборке, а n2 - количество элементов во второй выборке.
Далее вновь разделяем единый ранжированный ряд на два, состоящие соответственно из единиц первой и второй выборок, запоминая при этом значения рангов для каждой единицы. Подсчитываем отдельно сумму рангов, пришедшихся на долю элементов первой выборки, и отдельно - на долю элементов второй выборки. Определяем большую из двух ранговых сумм (Tx) соответствующую выборке с nx элементами.
Наконец, находим значение U-критерия Манна-Уитни по формуле:
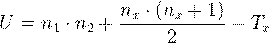
Полученное значение U-критерия сравниваем по таблице для избранного уровня статистической значимости (p=0.05 или p=0.01) с критическим значением U при заданной численности сопоставляемых выборок.
Если полученное значение U меньше табличного или равно ему, то признается статистическая значимость различий между уровнями признака в рассматриваемых выборках (принимается альтернативная гипотеза). Достоверность различий тем выше, чем меньше значение U.
Если же полученное значение U больше табличного, принимается нулевая гипотеза.
Критерий Уилкоксона для связанных выборок (Т-критерий Уилкоксона) – непараметрический статистический критерий, используемый для сравнения двух связанных (парных) выборок по уровню какого-либо количественного признака, измеренного в непрерывной или в порядковой шкале.
Суть метода состоит в том, что сопоставляются абсолютные величины выраженности сдвигов в том или ином направлении. Для этого сначала все абсолютные величины сдвигов ранжируются, а потом суммируются ранги. Если сдвиги в ту или иную сторону происходят случайно, то и суммы их рангов окажутся примерно равны. Если же интенсивность сдвигов в одну сторону больше, то сумма рангов абсолютных значений сдвигов в противоположную сторону будет значительно ниже, чем это могло бы быть при случайных изменениях.
Т-критерий Уилкоксона используется для оценки различий между двумя рядами измерений, выполненных для одной и той же совокупности исследуемых, но в разных условиях или в разное время. Данный тест способен выявить направленность и выраженность изменений - то есть, являются ли показатели больше сдвинутыми в одном направлении, чем в другом.
Классическим примером ситуации, в которой может применяться Т-критерий Уилкоксона для связанных совокупностей, является исследование "до-после", когда сравниваются показатели до и после лечения. Например, при изучении эффективности антигипертензивного средства сравнивается артериальное давление до приема препарата и после приема.
Условия и ограничения применения Т-критерия Уилкоксона:
1. Критерий Уилкоксона является непараметрическим критерием, поэтому, в отличие от парного t-критерия Стьюдента, не требует наличия нормального распределения сравниваемых совокупностей.
2. Число исследуемых при использовании T-критерия Уилкоксона должно быть не менее 5.
3. Изучаемый признак может быть измерен как в количественной непрерывной (артериальное давление, ЧСС, содержание лейкоцитов в 1 мл крови), так и в порядковой шкале (число баллов, степень тяжести заболевания, степень обсемененности микроорганизмами).
4. Данный критерий используется только в случае сравнения двух рядов измерений.








