Контрольные вопросы
1. Назначение, области применения и средства пакета Matlab в теоретических основах электротехники.
2. Запуск пакета Matlab и выход из него.
3. Виды сохраняемой информации и способы ее сохранения.
4. Рабочие окна пакета Matlab и работа с ними.
5. Понятие m-файла и Script-файла.
6. Работа с переменными в пакете Matlab.
6. Основные операции с матрицами в пакете Matlab.
7. Генерация векторов и массивов в пакете Matlab.
8. Основные пакеты расширения Matlab, используемые в электротехнике.
9. Создание графических объектов (функции plot () и hist ()).
10. Масштабирование и удаление графиков.
11. Совмещение нескольких графиков в одном окне.
12. Формы представления объектов в Control System Toolbox.
13. Операции над объектами в Control System Toolbox.
14. Действия с графическими окнами в Control System Toolbox и способы их выполнения.
15. Работа с графическими объектами в Control System Toolbox.
19. Понятие канонического вида дифференциального уравнения системы.
20. Порядок установки параметров блоков исследуемой модели системы.
21. Действия с блоками исследуемой модели системы.
22. Порядок сборки модели исследуемой системы.
24. Запись результатов моделирования в файл.
25. Методы контроля правильности модели.
Приложение 1
MATLAB как среда моделирования электрических цепей
1.1. Работа с ядром пакета прикладных программ Matlab
Общие сведения о ППП Matlab. Matlab – это сложный программный продукт, предназначенный для научных и инженерных расчетов.
Как всякому сложному понятию Matlabу трудно дать определение, охватывающее одновременно все его свойства. Можно лишь концептуально определить его основные свойства. С этой точки зрения Matlab – это:
- высокоэффективный язык инженерных и научных вычислений, поддерживающий математические вычисления, визуализацию научной графики и программирование с использованием легко осваиваемого операционного окружения, когда задачи и их решения могут быть представлены в нотации, близкой к математической;
– язык программирования, позволяющий написание программ и функций для многократного использования в виде m-файлов, из которых по мере увеличения их количества формируются пакеты прикладных программ (ППП) в виде коллекций m-файлов для решения определенной задачи или проблемы;
- операционная среда.
Наиболее известные области применения системы Matlab:
– математика и вычисления;
– разработка алгоритмов;
– вычислительный эксперимент, имитационное моделирование, макетирование;
– анализ данных, исследование и визуализация результатов;
– научная и инженерная графика;
– разработка приложений, включая графический интерфейс пользователя.
Одним из направлений ее использования является решение математических задач теории цепей и силовой электроники. Особенностями этого направления являются большая скорость и прозрачность технологий вычислений.
Далее описывается работа с Matlab 7.9.0 ( R 2009) (далее Matlab) и лишь в части, касающейся обеспечения выполнения лабораторных работ по дисциплине «Теоретическме основы электротехники». В настоящей работе рассматривается работа с ядром Matlab и его приложением Simulink, другие аспекты его использования рассматриваются в следующих лабораторных работах.
Для запуска Matlab необходимо найти на рабочем столе ярлык этой программы и запустить его на выполнение, при этом откроется рабочее окно программы, общий вид которого показан на рис. 1
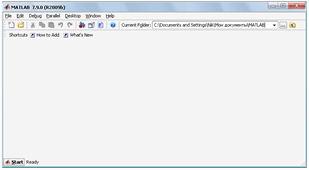
Рис. 1. Командное окно системы M atlab
Здесь же показано ниспадающее меню File. Оно
содержит опции, приведенные в табл.1.
Некоторые из команд подопций могут быть вызваны с помощью комбинаций «горячих клавиш», указанных в меню.
Таблица 1
Основные опции командного окна системы Matlab
| Опция | Подопции | Назначение | |
| New | Blank M-file Function M-file Class M-file Figure Variable Model GUI Deployment Project | Открыть в редакторе/отладчике новый файл Создать М-файл функции Определить класс для М-файла функции Открыть графическое окно Показать переменные текущейсесии Открыть окно доля создания новой модели Открыть графический интерфейс пользователя Создать/открыть файл проекта | |
| Open | Открыть в редакторе/отладчике указанный файл | ||
| Import Data… | Импортировать данные из файла | ||
| Save Workspace As… | Вызов окна сохранения m-файла | ||
| Set Path… | Вызов средства просмотра путей доступа PathBrowser | ||
| Preferences … | Выбор характеристик | ||
| Page Setup… | Формат страницы вывода на печать | ||
| | Установка опций вывода на печать | ||
| PrintSelection | Печать выделенного фрагмента | ||
| Exit MATLAB | Окончание текущей сессии | ||
Для отображения всех действий и результатов при выполнении расчетов в Matlab используются четыре рабочих окна:
- окно команд (Command Window);
- рабочее пространство (Workspace);
- окно истории текущей сессии (Command History);
-окно текущей папки (Current Folder).
Каждое из них может быть выведено на полный экран щелчком левой кнопки мыши на значке  , убрано в исходное состояние – щелчком левой кнопки мыши на значке
, убрано в исходное состояние – щелчком левой кнопки мыши на значке  , а убрано из рабочего окна М atlab– щелчком левой кнопки мыши на значке
, а убрано из рабочего окна М atlab– щелчком левой кнопки мыши на значке  соответствующего окна. При этом в разделе Desktop основного меню программы производится сброс соответствующих флажков вызова окон в рабочее окно программы. Восстановление каждого из окон производится повторной установкой флажков в разделе меню Desktop, а одновременно всех окон по умолчанию – последовательностью Desktop – DesktopLayout – Default.
соответствующего окна. При этом в разделе Desktop основного меню программы производится сброс соответствующих флажков вызова окон в рабочее окно программы. Восстановление каждого из окон производится повторной установкой флажков в разделе меню Desktop, а одновременно всех окон по умолчанию – последовательностью Desktop – DesktopLayout – Default.
В окне Command History сохраняются все набранные в процессе текущей сессии команды, что позволяет использовать их повторно в окне Command Window в исходном или модифицированном виде.
В окне рабочего пространства Workspace сохраняются имена всех использованных в текущей сессии переменных.
Подсказка «>>» в окне команд Command Window является приглашением системы и показывает готовность системы к выполнению команд. После набора простейших математических выражений в естественной форме записи и нажатия клавиши Enter на экране сразу же появляется результат. Самó выражение может быть записано в двух видах:
Выражение
или
Имя переменной=Выражение
В первом случае на самом деле результат выражения присваивается специальной служебной переменной имеющей имя ans (answer – ответ). Эту переменную также можно использовать в расчетах.
Во втором случае результат не только вычисляется, но и присваивается указанной переменой. Matlab не требует от пользователя специальных команд для объявления переменных, они создаются автоматически при первом указании пользователем их имени. Если результаты промежуточных выражений выводить на экран не нужно, то необходимо поставить в конце выражения символ «;».
Команды набора и редактирования команд в Matlab такие же, как в любом другом оконном редакторе Windows, например в блокноте. Например, Matlab предоставляет пользователю возможность пролистать предыдущие команды, сделать это можно с помощью клавиш Page Up и Page Down. В эти команды легко можно внести изменения и повторно их выполнить.
Работа с командным окном Matlab. Командное окно можно использовать для текущих вычислений в режиме калькулятора. Для этого в командной строке вводится математическое выражение. После нажатия Enter будет выведен результат. В системе Matlab используются традиционные арифметические операции +,–,*,/, а также операция возведения в степень ^. Для определения приоритета выполнения операций в выражении можно использовать круглые скобки. При вводе дробных чисел используется десятичная точка (не запятая!).
Кроме того, в выражении можно использовать встроенные функции системы Matlab. Количество этих функций превышает 1000 наименований. В табл.2 - 6 приведены некоторые из функций, часто используемых при решении различных задач.
Таблица 2
Элементарные функции в Matlab
(Большими буквами обозначены массивы, малыми – элемент массива или число)
| Имя | Вычисление |
| Функции работы с числами | |
| abs(x) | абсолютных значений действительных и комплексных чисел |
Продолжение табл.2
| real(z) | действительной части комплексного числа | ||
| imag(z) | мнимой части комплексного числа | ||
| mod(x,y) | целой части от деления чисел | ||
| rem(x,y) | остатка от деления чисел | ||
| pov2(z) | степеничисла 2 | ||
| sqrt(z) | квадратного корня | ||
| exp(z) | e в степени z | ||
| log2(z) | двоичногологарифмачисла | ||
| log10(z) | десятичного логарифма числа | ||
| log(z) | натурального логарифма числа | ||
| expm(Z) | матричной экспоненты (e в степени Z, где Z– матрица) | ||
| angle(Z) | аргумента комплексного числа в радианах | ||
| conj(Z) | числа, комплекно-сопряженного Z | ||
| sign(X) |
| ||
| Имя | Вычисление | ||
| Функции работы с векторами | |||
| primes(n) | простых чисел в интервале от 0 до n | ||
| icm(m,n) | наименьшего общего кратного чисел m и n | ||
| icm(A,B) | наименьшего общего кратного чисел в массивах A и B | ||
| perms(V) | матрицы перестановок элементов вектора V | ||
| pov2([M,N]) | массивачисел M.*(2^N) | ||
| length(V) | длины вектора Р | ||
| prod (V) | произведения элементов вектора Р | ||
| sum (V) | суммы элементов вектора Р | ||
| Функции работы с матрицами | |||
| tril (A) | создание нижней треугольной матрицы | ||
| triu (A) | создание верхней треугольной матрицы | ||
Окончание табл.2
| fliplr (A) | вращение матрицы относительно вертикальной плоскости |
| flipud (A) | то же, относительно горизонтальной плоскости |
| A‘ | транспонирование матрицы А |
| eig (A) | вычисление собственных чисел матрицы А |
| poly (A) | формирование характеристического полинома матрицы А |
| poly (eig (A)) | то же, по ее собственным значениям |
| size (A) | вычисление размерности матрицы А |
| Преобразование координат | |
| [T,R]=cart2pol(x,y) | Преобразование 2-мерных декартовых координат x, y и полярныеT, R (T – угол в рад.) |
| [T,R,Z]=cart2pol(x,y,z) | То же, для трехмерных координат |
| [X,Y]=pol2cart(T,R) | Преобразование полярных координат T, R в декартовыX, Y |
| [X,Y,Z]=pol2cart(T,R,Z) | То же, для трехмерных координат |
Таблица 3
Функции линейной алгебры в Matlab
| Имя | Вычисление | |
| inv(A) | обратной матрицы | |
| pinv(A) | псевдообратной матрицы | |
| det(A) | определителя матрицы | |
| rank(A) | ранга матрицы | |
| trace(A) | следа матрицы | |
| norm(A) | нормы матрицы | |
| size(A) | размера матрицы | |
| jordan(A) | Жордановой формы матрицы | |
| poly(A) | характеристического полинома матрицы | |
| eig(A) | собственных векторов (значений) матрицы | |
| cond(A) | числа обусловленности матрицы | |
| null(A) | базиса ядра матрицы | |
Таблица 4
Функции работы с полиномами в Matlab
| Имя | Вычисление |
| polyval(a) | полинома в точке а |
| poly(P) | восстановление полинома по корням |
| roots(P) | корней полинома |
| conv(P) | свертки (произведения) полинома |
| deconv(P) | деления полиномов |
| polyder(P) | производной полинома |
| residue(P) | разложения отношения полиномов в сумму простых дробей |
Таблица 5
Функции работы с дифференциальными уравнениями в Matlab
| Имя | Вычисление |
| diff() | конечных разностей произвольного порядка |
| gradient() | аналога градиента |
| del2() | оператора Лапласа |
| trapz() | определенного интеграла методом трапеций |
| quad() | определенного интеграла методом парабол |
| ode 45() | вызов решателя задачи Коши |
| ode 23() | вызов решателя задачи Коши |
| ode 113() | вызов решателя задачи Коши |
| ode 15s() | вызов решателя задачи Коши |
| ode 23s() | вызов решателя задачи Коши |
| ode 23t() | вызов решателя задачи Коши |
| ode 23tb() | вызов решателя задачи Коши |
| bvp4c() | вызов решателя краевой задачи системы ОДУ |
| fzero() | корня нелинейного уравнения |
| fsolve() | решения системы нелинейных уравнений |
| fminbnd() | минимума |
| fminsearch() | многомерного минимума |
Таблица 6
Функции проектирования и моделирования систем управления в Matlab
| Имя | Вычисление |
| tf | передаточной функции в tf-форме |
| zpk | передаточной функции в zpk-форме |
| ss | передаточной функции в ss-форме |
| dss | дискретной передаточной функции в ss-форме |
| frd | передаточной функции в frd-форме |
| tfdata | числителя и знаменателя передаточной функции |
| zpkdata | нулей и полюсов передаточной функции |
| ssdata | матриц пространства состояний |
| frdata | частот и откликов |
| parallel | передаточной функции параллельного соединения |
| series | передаточной функции последовательного соединения |
| feedback | передаточной функции соединения с ОС |
| append | объединения подсистем |
| ltiview | активация графического интерфейса |
| bode | годографа системы (диаграммы Боде) |
| nyquist | диаграммы Найквиста |
| nichols | диаграммы Никольса |
| place | вектора обратной связи для заданных полюсов |
| kalman | наблюдателя Калмана |
| ctrb | матрицы управляемости |
| obsv | матрицы наблюдаемости |
| canon | канонического представления в пространстве состояний |
| step | переходной функции |
| impulse | весовой функции |
| initial | отклика системы на начальные условия |
| lsim | отклика системы на заданное воздействие |
Общие правила вычислений в командном окне сводятся к следующему:
1. Работа с системой в режиме прямых вычислений носит диалоговый характер и происходит по правилу «задал выражение, получи ответ».
2.Пользователь набирает на клавиатуре вычисляемое выражение, редактирует его (если нужно) в командной строке и завершает ввод нажатием клавиши Enter. Для указания текущего места ввода и вычисления используется символ >>на пустой строке. В предшествующих месту ввода строках редактирование выражений и вычисления невозможны.
3. Данные вводятся с помощью строчного редактора, (встроенного в Matlab (по умолчанию) или внешнего, выбираемого пользователем).
4. Знаком присваивания является привычный математикам знак равенства =, а не комбинированный знак :=, как во многих других математических системах.
5. Правила записи матрицы, вектора и скаляра: большими буквами (например, А) обозначаются матрицы, малыми (а) – векторы и скаляры. Векторные функции(выдающие значения в виде вектора) обозначаются большими буквами (F(x)), скалярные функции(их значение – скаляр – действительное число) обозначаются малыми буквами (f(x)).
6. Комплексное или мнимое число определяется по наличию в его составе констант i или j, которым присваивается значение
qrt(-1) = √ -1.
Комплексное число можно вводить одним из следующих способов:
5+3 i; 5+3* I; 5+3 j; 5+3* j
или
5+3* sqrt (-1).
7. Значения аргумента функции в виде выражения присваивания вводятся раньше выражения функции и отделяются от него точкой с запятой (см. далее пп.11-13). Аргумент в виде одного числа можно вставлять в окаймлении круглых скобок непосредственно в выражение функции. Правильный ввод простейшего вычисляемого выражений
y = sin (0.35) Enter
или
sin (0.35) Enter.
Если аргументов несколько, то они отделяются запятыми. Если вычисляемых функций несколько в одном месте ввода, то они отделяются запятыми.
8. Арифметические операции для массивов отличаются от матричных операций наличием точки перед знаком операции:
–А.*Б (умножение массивов – массивы должны иметь одинаковое количество чисел или один из них должен быть числом);
–А./Б (деление);
–А.\Б (левое деление);
–А.^Б (возведение в степень).
Точка перед «+» и «–» не ставится!
9. Встроенные функции (например, sin) записываются строчными буквами и их аргументы указываются в круглых скобках (см. табл.2). Если аргументов несколько, то они отделяются запятыми.
10. Для изменения формата вывода результата вычисления необходимо до нажатия клавиши Enter установить нужный формат через меню «Файл  Свойства».
Свойства».
11. Для блокировки вывода результата некоторого выражения (ввиду промежуточного характера) после него надо установить знак; (точка с запятой): если блокировка отсутствует, то Matlab выдаст результат расчета по части выражения до неустановленного знака и сообщение об ошибке, а остальную часть вычисляемого выражения игнорирует, как показано на рис. 2, в.
а) »x = [0.5 0.7 1];
Y = sin(x)
Y = 0.4794 0.6442 0.8415
б) »x = [0.5 0.7 1; 1 3 12; 0.8 0.1 3];
Y = sin(x)
Y = 0.4794 0.6442 0.8415
0.8415 0.1411 –0.5366
0.7174 0.0998 0.1411
в) »x = [0.5 0.7 1]
Y = sin(x)
??? x = [0.5 0.7 1] Y = sin(x)
Error: Missing MATLAB operator
Рис. 2. Правильная запись вычисления функции на одномерном (а) и
многомерном (б) массивах и неправильная (в) (пропуск точки с запятой после первого оператора)
12. Если не указана переменная для значения результата вычислений, то Matlab назначает такую переменную с именем ans.
13. Результат вычислений выводится в строках вывода (без знака >>).
14. Для вычисления функции на одномерном или многомерном матричных массивах значений аргумента необходимо выполнить действия согласно рис.13.
В векторе (одномерном массиве) значения заключены в квадратные скобки и отделяются друг от друга пробелом (рис.3, а); в матрице (многомерном массиве) значения заключены тоже в квадратные скобки, причем, строки отделяются точкой с запятой (порядок следования строк: левая выше правой), а значения в каждой строке отделяются аналогично вектору (рис.3, б).
15. Если значения аргумента вычисляемой функции являются членами отрезка арифметической прогрессии с заданной разностью (шагом), то для записи аргумента применяется оператор «:» (двоеточие), как показано на рис. 3. При разности, равной единице, ее запись в операторе можно опускать (рис. 3, б).
а) » x=[1:2.5:16.5];
Y=sin(x)
Y =
0.8415 –0.3508 –0.2794 0.7985 –1.0000 0.8038 –0.2879
б) » x=1:10;
Y=sin(x)
Y = Columns 1 through 7
0.8415 0.9093 0.1411 –0.7568 –0.9589 –0.2794 0.6570
Columns 8 through 10
0.9894 0.4121 –0.5440
в) x =[1:2.5:11.5; 2:6];
Y = sin ( x )
Y = 0.8415 -0.3508 -0.2794 0.7985 -1.0000 0.9093 0.1411 -0.7568 -0.9589 -0.2794
Рис. 3. Правильная запись вычисления функции на одномерном массиве аргумента в виде отрезка арифметической прогрессии (с разностями 2,5 (а) и 1 (б)) и в виде 2-строчной матрицы с теми же разностями (в)
Для правильной записи значений матрицы аргумента, когда ее строки являются отрезками арифметических прогрессий, необходимо руководствоваться правилами 14 и 15 одновременно.
16. Комментарии записываются в отдельную строку, помечаемую знаком «%» (процент) в первом знакоместе строки (см. рис. 4, а).
Разбиение строки с длинным выражением или комментарием на две производится установкой курсора перед переносимой на создаваемую вторую строку частью выражения и нажатием клавиш Shift + Enter (рис. 4, б) – двукратное разбиение выражения х = [23 45 67 45] на три строки).
17. Соединение двух строк в одну в программе или в выражении производится установкой курсора в начало второй строки и нажатием клавиш Shift + Backspace. Эта операция над строками с выражениями 67 и 45 показана рис. 4, в.
а)»x=[0.5 0.7 1];
Y=sin(x)
% Комментарии размещаются в отдельных строках
Y =
0.4794 0.6442 0.8415
б)» x=[23 45 67 45]
x=[23 45
67
45]
в)» x=[23 45 67
45]
Рис. 4. Ввод комментария в вычисляемое выражение или программу (а), разбиение первой строки на три (б), объединение 3-й и 2-й строк (в)
18. Вычисляемое выражение сразу после завершения вычисления можно ввести вновь в текущее место ввода нажатием кнопки «стрелка вверх» ↑(для изменения величин аргументов или коррекции выражения).
Повторное нажатие кнопки ↑ заменит текущие условия на условия, им предшествующие: этот процесс можно повторять многократно, добиваясь вызова в место ввода все более ранних вычислительных условий.
Ранее вытеснявшееся выражение можно быстро вставить в место ввода путем выделения его левой кнопкой мышки (кнопка далее отпускается) и небольшого протягивания его вниз повторно нажатой левой кнопкой: Matlab сам вставит выделенное выражение.
19. Ранее примененную функцию можно вставить в командное окно через копирование её из окна Command History (Протокола команд), в котором все ранее использованные команды и функции сохраняются до тех пор, пока пользователь не удалит их.
20. Чтобы сохранить данные вычислений в окне управления (выражения, программы, результаты или их части) для повторного вызова и работы, необходимо:
− выделить данные,
− скопировать их в буфер,
− вызвать редактор-отладчик m-файлов через меню «Файл-Создать- m -файл», либо командой edit в командном окне,
− вставить скопированные данные в открывшийся новый m-файл и сохранить его через меню редактора File - SaveAs … («Файл-Сохранить как»).
21. Для продолжения вычислительной работы в окне управления с данными, сохраненными по правилам п.20, необходимо через меню «Файл-Открыть» открыть требуемый файл, выделить в нем требуемые для работы фрагменты, скопировать их в буфер и вставить в текущее место ввода окна управления.
Рассмотрим применение перечисленных выше правил для выполнения вычислений.
Использование переменных. Результат вычислений можно присвоить любой переменной, определенной пользователем. Имя переменной должно начинаться с буквы и может состоять из букв, цифр и символа подчеркивания. Система Matlab различает строчные и прописные буквы в именах переменных (A и a – это разные переменные). Знак = соответствует операции присваивания. Значения переменных, вычисленные в течение текущего сеанса работы, сохраняются в специально зарезервированной области памяти компьютера, называемой рабочим пространством (Workspace). Использование переменных рассмотрено в примере 1.
Пример 1. Использование переменных
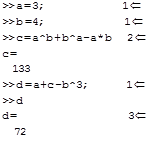
Комментарии к вычислениям:
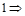 Если в конце строки ставится точка с запятой, то результат не будет выведен после нажатия Enter.
Если в конце строки ставится точка с запятой, то результат не будет выведен после нажатия Enter.
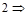 Здесь нет точки с запятой, и после нажатия Enter результат выводится и присваивается переменной c.
Здесь нет точки с запятой, и после нажатия Enter результат выводится и присваивается переменной c.
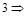 Для того чтобы узнать значение переменной достаточно ввести ее имя в командную строку и нажать Enter.
Для того чтобы узнать значение переменной достаточно ввести ее имя в командную строку и нажать Enter.
Использование Matlab как калькулятора иллюстрирует также пример 2.
Пример 2. Использование Matlab как калькулятора
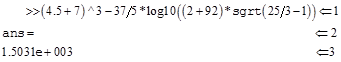
Комментарии к вычислениям:
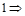 Нажатие клавиши Enter.
Нажатие клавиши Enter.
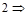 Результат присваивается переменной с именем ans
Результат присваивается переменной с именем ans
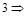 Результат выводится в формате с плавающей точкой. Такая запись означает 1,5031·103.
Результат выводится в формате с плавающей точкой. Такая запись означает 1,5031·103.
Длинные выражения можно записать в нескольких строках с использованием в качестве знака переноса символа многоточия ….
Использование массивов . В системе Matlab также используются массивы, математической формой представления которых являются матрицы. Напомним основные действия над матрицами и их реализацию в Matlab.
1. Присвоение значений матрице. Простейшей операцией с матрицей является ее создание. Для создания столбца необходимо указать его имя, знак равенства и в квадратных скобках через запятую или через пробел перечислить значения элементов. Например:
A=[1 2 3 4 5]
A =
1 2 3 4 5
В случае, если необходимо создать столбец чисел, то в качестве разделителя используется символ «;» (точка с запятой), например:
A =[1;2;3;4;5]
A =
1
2
3
4
5
Для создания квадратной или прямоугольной матрицы необходимо чередовать оба этих способа, например:
C=[1 2 3;4 5 6;7 8 9]
C =
1 2 3
4 5 6
7 8 9.
2. Создание матриц специального вида. В математике встречаются матрицы специального вида, часто используемые при решении прикладных задач. Ниже приведен ряд из них.
Единичная матрица, рис. 5, а. В единичной матрице все элементы
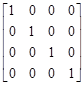
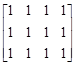
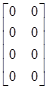
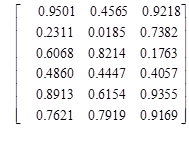
а б в г
Рис. 5. Специальные матрицы
равны нулю, кроме элементов стоящих на главной диагонали и равных единице. Для создания единичной матрицы необходимо подать команду
<Имя матрицы>=eye(<размер>).
Например: A = eye (4).
Единичная матрица может быть только квадратной.
Матрица со всеми единицами, рис. 5, б. Эта матрица содержит единицы во всех ячейках. Для создания матрицы необходимо указать
Имя матрицы=ones(Кол-во строк, Кол-во столбцов)
Например: A=ones(3, 4).
Нулевая матрица, рис. 5, в. Эта матрица содержит во всех своих ячейках одни нули. Для создания необходимо выполнить следующую команду:
Имя матрицы=zeros(кол-во строк, кол-во столбцов)
Например: A=zeros(4, 2).
Случайная матрица, рис. 5, г. Все значения этой матрицы получаются с генератора случайных чисел. Для создания такой матрицы необходимо задать следующую команду:
Имя матрицы=rand(кол-во строк, кол-во столбцов)
Например: A=rand(6, 3). По умолчанию в качестве элементов матрицы используются вещественные числа.
Доступ к ячейкам матрицы. Для доступа к ячейкам матрицы необходимо указать имя матрицы, номер строки и номер столбца. Нумерация строк и столбцов ведется с единицы. Номера пишутся в круглых скобках. Общий формат записи









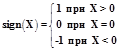 – для действительных чисел
– для действительных чисел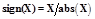 – для комплексных чисел
– для комплексных чисел