Тест по собственным векторам (10-е занятие)
1. Линейный оператор 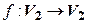 в базисе
в базисе 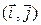 имеет матрицу
имеет матрицу 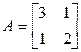 . Какие из перечисленных векторов будут собственными векторами оператора
. Какие из перечисленных векторов будут собственными векторами оператора 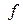 ? Какие у них собственные значения?
? Какие у них собственные значения?
а) 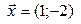 ; б)
; б) 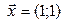 ; в)
; в) 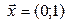 ; г) таких нет.
; г) таких нет.
2. Линейный оператор 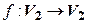 в базисе
в базисе 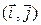 имеет матрицу
имеет матрицу 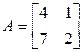 . Характеристический многочлен этого оператора имеет вид:
. Характеристический многочлен этого оператора имеет вид:
а) 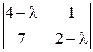 ; б)
; б) 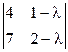 ; в)
; в) 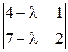 ; г)
; г) 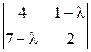 ; д) другой ответ.
; д) другой ответ.
3. Пусть 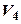 – комплексное линейное пространство и пусть линейный оператор
– комплексное линейное пространство и пусть линейный оператор 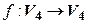 имеет характеристический многочлен
имеет характеристический многочлен 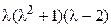 . Собственными значениями оператора
. Собственными значениями оператора 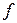 будут следующие:
будут следующие:
а) 0; б) 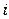 ; в)
; в) 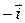 ; г) 2; д) 6; е) другой ответ.
; г) 2; д) 6; е) другой ответ.
4. Пусть 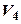 – действительное линейное пространство и пусть линейный оператор
– действительное линейное пространство и пусть линейный оператор 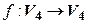 имеет характеристический многочлен
имеет характеристический многочлен 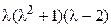 . Собственными значениями оператора
. Собственными значениями оператора 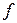 будут следующие:
будут следующие:
а) 0; б) 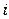 ; в)
; в) 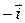 ; г) 2; д) 6; е) другой ответ.
; г) 2; д) 6; е) другой ответ.
5. Характеристический многочлен некоторого линейного оператора имеет вид 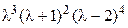 . Кратность его собственного значения
. Кратность его собственного значения 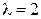 равна:
равна:
а) 0; б) 1; в) 2; г) 3; д) 4; е) 5; ж) другой ответ.
6. Пусть кратность собственного значения 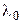 линейного оператора
линейного оператора 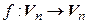 равна 4. Количество линейно независимых собственных векторов с этим собственным значением может равняться:
равна 4. Количество линейно независимых собственных векторов с этим собственным значением может равняться:
а) 0; б) 1; в) 2; г) 3; д) 4; е) 5; ж) другой ответ.
7. Пусть кратность собственного значения 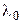 линейного оператора
линейного оператора 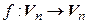 равна 3 и пусть существует два линейно независимых собственных вектора с этим собственным значением. Базис линейного пространства
равна 3 и пусть существует два линейно независимых собственных вектора с этим собственным значением. Базис линейного пространства 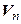 , состоящий из собственных и присоединенных векторов оператора
, состоящий из собственных и присоединенных векторов оператора 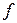 , содержит следующие векторы, соответствующие этому собственному значению:
, содержит следующие векторы, соответствующие этому собственному значению:
а) три собственных; б) два собственных и один присоединенный; в) один собственный и два присоединенных; г) три присоединенных; д) другой ответ.
8. Линейный оператор 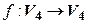 в некотором базисе имеет матрицу А. Если этот оператор имеет собственные значения
в некотором базисе имеет матрицу А. Если этот оператор имеет собственные значения 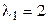 ,
, 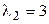 ,
, 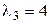 и
и 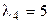 , то:
, то:
а) А приводится к диагональному виду; б) А не приводится к диагональному виду; в) для верного ответа не хватает информации.
9. Линейный оператор 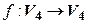 в некотором базисе имеет матрицу А. Если этот оператор имеет собственные значения
в некотором базисе имеет матрицу А. Если этот оператор имеет собственные значения 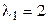 кратности 3 и
кратности 3 и 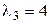 , причем
, причем 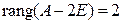 , то:
, то:
а) А приводится к диагональному виду; б) А не приводится к диагональному виду; в) для верного ответа не хватает информации.
10. Линейный оператор 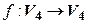 в некотором базисе имеет матрицу А. Если этот оператор имеет собственные значения
в некотором базисе имеет матрицу А. Если этот оператор имеет собственные значения 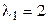 кратности 3 и
кратности 3 и 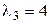 , причем
, причем 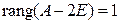 , то:
, то:
а) А приводится к диагональному виду; б) А не приводится к диагональному виду; в) для верного ответа не хватает информации.
11. Жорданова клетка 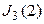 это:
это:
а) 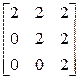 ; б)
; б) 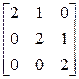 ; в)
; в) 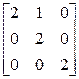 ; г)
; г) 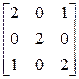 ; д)
; д) 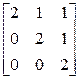 ; е)
; е) 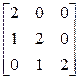 .
.
12. Матрица 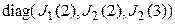 это:
это:
а) 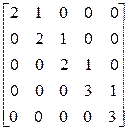 ; б)
; б) 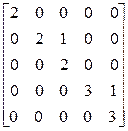 ; в)
; в) 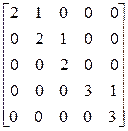 ; г)
; г) 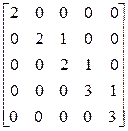 ; д)
; д) 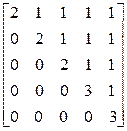 ; е)
; е) 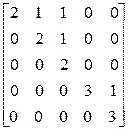 .
.
13. Квадратная матрица 5-го порядка имеет собственное значение 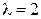 кратности 5, причем ему соответствует 5 линейно независимых собственных векторов. Жорданова нормальная форма этой матрицы имеет вид:
кратности 5, причем ему соответствует 5 линейно независимых собственных векторов. Жорданова нормальная форма этой матрицы имеет вид:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж)  .
.
14. Квадратная матрица 5-го порядка имеет собственное значение 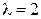 кратности 5, причем ему соответствует 4 линейно независимых собственных вектора. Жорданова нормальная форма этой матрицы имеет вид:
кратности 5, причем ему соответствует 4 линейно независимых собственных вектора. Жорданова нормальная форма этой матрицы имеет вид:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  .
.
15. Квадратная матрица 5-го порядка имеет собственное значение 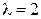 кратности 5, причем ему соответствует 3 линейно независимых собственных вектора и у одного из них есть присоединенный. Жорданова нормальная форма этой матрицы имеет вид:
кратности 5, причем ему соответствует 3 линейно независимых собственных вектора и у одного из них есть присоединенный. Жорданова нормальная форма этой матрицы имеет вид:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  .
.
16. Квадратная матрица 5-го порядка имеет собственное значение 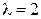 кратности 5, причем ему соответствует 3 линейно независимых собственных вектора и у двух из них есть присоединенные. Жорданова нормальная форма этой матрицы имеет вид:
кратности 5, причем ему соответствует 3 линейно независимых собственных вектора и у двух из них есть присоединенные. Жорданова нормальная форма этой матрицы имеет вид:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  .
.
17. Квадратная матрица 5-го порядка имеет собственное значение 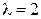 кратности 5, причем ему соответствует 2 линейно независимых собственных вектора и у одного из них есть присоединенные. Жорданова нормальная форма этой матрицы имеет вид:
кратности 5, причем ему соответствует 2 линейно независимых собственных вектора и у одного из них есть присоединенные. Жорданова нормальная форма этой матрицы имеет вид:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  .
.
18. Квадратная матрица 5-го порядка имеет собственное значение 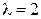 кратности 5, причем ему соответствует 2 линейно независимых собственных вектора и они оба имеют присоединенные. Жорданова нормальная форма этой матрицы имеет вид:
кратности 5, причем ему соответствует 2 линейно независимых собственных вектора и они оба имеют присоединенные. Жорданова нормальная форма этой матрицы имеет вид:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж)  .
.
19. Квадратная матрица 5-го порядка имеет собственное значение 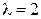 кратности 5, причем ему соответствует один линейно независимый собственный вектор. Жорданова нормальная форма этой матрицы имеет вид:
кратности 5, причем ему соответствует один линейно независимый собственный вектор. Жорданова нормальная форма этой матрицы имеет вид:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  .
.








