Учащихся младших классов с натуральным числом

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

1. НАУЧНО-ТЕОРЕТИЧ ЕСКИЕ ОСНОВЫ ОЗНАКОМЛЕНИЯ

УЧАЩИХСЯ МЛАДШИХ КЛАССОВ С НАТУРАЛЬНЫМ ЧИСЛОМ

1.1. Число, как основное понятие математики

Число является одним из основных понятий математики. Понятие числа развивалось в тесной связи с изучением величин, эта связь сохраняется и те­перь. Во всех разделах современной математики приходится рассматривать разные величины и пользоваться числами

Существует большое количество определений понятию «число».

Первое научное определение числа дал Эвклид в своих «Началах», ко­торое он, очевидно, унаследовал от своего соотечественника Эвдокса Книдского (около 408 - около 355 гг. до н. э.): «Единица есть то, в соответствии с чем каждая из существующих вещей называется одной. Число есть множество, сложенное из единиц». Так определял понятие числа и русский математик Маг­ницкий в своей «Арифметике» (1703 г.). [4; 36с]

Еще раньше Эвклида Аристотель дал такое определение: «Число есть множество, которое измеряется с помощью единиц» [4; 54].

Со слов греческого философа Ямвлиха, еще Фалес Милетский - родо­начальник греческой стихийно-материалистической философии учил, что «число есть система единиц». Это определение было известно и Пифагору.

В своей «Общей арифметике» (1707 г) великий английский физик, ме­ханик, астроном и математик Исаак Ньютон пишет: «Под числом мы подра­зумеваем не столько множество единиц, сколько абстрактное отношение какой-нибудь величины к другой величине такого же рода, взятой за единицу. Число бывает трех видов: целое, дробное и иррациональное. Целое число есть то, что измеряется единицей; дробное - кратной частью единицы, иррациональное -число, не соизмеримое с единицей». [4; 38]

Мариупольский математик С.Ф. Клюйков также внес свой вклад в опре­деление понятия числа: «Числа - это математические модели реального мира,

придуманные человеком для его познания». Он же внес в традиционную клас­сификацию чисел так называемые «функциональные числа», имея в виду то, что во всем мире обычно именуют функциями.

Ниже представлена схема развития понятия числа (Рис.1)

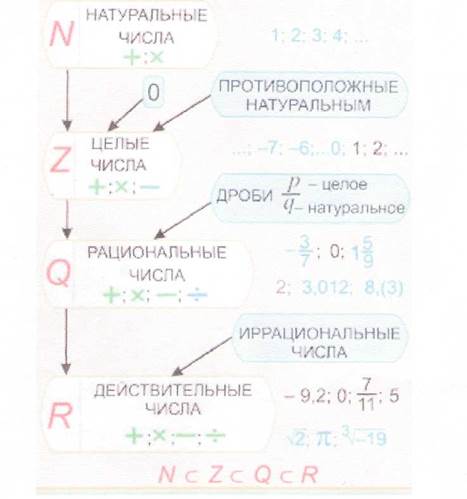
Рис.1 Схема развития понятия числа.

Из схемы видно, что к основным видам чисел относятся:

Ø Натуральные числа , получаемые при естественном счёте; множество
натуральных чисел обозначается N Т.о. N ⁼ {1,2, 3, ...}. Натуральные
числа замкнуты относительно сложения и умножения (но не вычитания
или деления). Натуральные числа коммутативны и ассоциативны относительно сложения и умножения, а умножение натуральных чисел дистри­бутивно относительно сложения.

Ø Целые числа, получаемые объединением натуральных чисел с множеством отрицательных чисел и нулём, обозначаются

Z = {… - 2, - 1, 1, 2, …}. Целые числа замкнуты относительно сложе­ния, вычитания и умножения (но не деления).

Ø Рациональные числа — числа, представимы в виде дроби m/n (n^O), где
тип — целые числа. Для рациональных чисел определены все четыре
«классические» арифметические действия: сложение, вычитание, умножение и деление (кроме деления на ноль). Для обозначения рациональ­ных чисел используется знак Q.

Ø Действительные (вещественные) числа представляют собой расширение множества рациональных чисел, замкнутое относительно некоторых (важных для математического анализа) операций предельного перехода. Множество вещественных чисел обозначается R. Его можно рассматри­вать как пополнение поля рациональных чисел Q при помощи нормы, яв­ляющейся обычной абсолютной величины. Кроме рациональных чисел, R включает множество иррациональных чисел, не представимых в виде отношения целых. Кроме подразделения на рациональные и иррацио­нальные, действительные числа также подразделяются на алгебраические и трансцендентные. При этом каждое трансцендентное число является иррациональным, каждое рациональное число — алгебраическим.

1.2. Понятие натурального числа

Согласно общепринятому определению число - важнейшее математическое понятие. Возникнув в простейшем виде ещё в первобытном обществе, понятие числа изменялось на протяжении веков, постепенно обогащаясь содержанием по мере расширения сферы человеческой деятельности и связанного с ним расширения круга вопросов, требовавшего количественного описания и иссле­дования. На первых ступенях развития понятие числа определялось потребно­стями счёта и измерения, возникавшими в непосредственной практической

деятельности человека. Затем число становится основным понятием математики, и дальнейшее развитие понятия числа определяется потребностями этой науки.

Понятие натурального числа, вызванное потребностью счёта предметов, возникло ещё в доисторические времена. Процесс формирования понятия нату­рального числа протекал в общих чертах следующим образом. На низшей сту­пени первобытного общества понятие отвлечённого числа отсутствовало. Это не значит, что первобытный человек не мог отдавать себе отчёта о количестве предметов конкретно данной совокупности, например о количестве людей, уча­ствующих в охоте, о количестве озёр, в которых можно ловить рыбу, и т.д. Но в сознании первобытного человека ещё не сформировалось то общее, что есть в объектах такого рода, как, например, "три человека", "три озера" и т.д.

Анализ языков первобытных народностей показывает, что для счёта пред­метов различного рода употреблялись различные словесные обороты. Слово "три" в контекстах "три человека", "три лодки" передавалось различно. Конеч­но, такие именованные числовые ряды были очень короткими и завершались неиндивидуализированным понятием ("много") о большом количестве тех или других предметов, которое тоже являлось именованным, т. е, выражалось раз­ными словами для предметов разного рода, такими, как "толпа", "стадо", "куча" и т.д.

Источником возникновения понятия отвлечённого числа является прими­тивный счёт предметов, заключающийся в сопоставлении предметов данной конкретной совокупности с предметами некоторой определённой совокупно­сти, играющей как бы роль эталона. У большинства народов первым таким эта­лоном являются пальцы ("счёт на пальцах"), что с несомненностью подтвер­ждается языковедческим анализом названий первых чисел. На этой ступени число становится отвлечённым, не зависящим от качества считаемых объектов, но вместе с тем выступающим во вполне конкретном осуществлении, связан­ном с природой эталонной совокупности. [4; 25с]

Расширяющиеся потребности счёта заставили людей употреблять другие счётные эталоны, такие, как, например, зарубки на палочке. Для фиксации

сравнительно больших чисел стала использоваться новая идея - обозначение некоторого определённого числа (у большинства народов - десяти) новым зна­ком, например зарубкой на другой палочке. С развитием письменности воз­можности воспроизведения числа значительно расширились. Сначала числа стали обозначаться чёрточками на материале, служащем для записи (папирус, глиняные таблички и т.д.). Затем были введены другие знаки для больших чи­сел. Вавилонские клинописные обозначения чисел, так же, как и сохранившие­ся до наших дней "римские цифры", ясно свидетельствуют именно об этом пути формирования обозначений для чисел. Шагом вперёд была индийская позици­онная система счисления, позволяющая записать любое натуральное число при помощи десяти знаков - цифр. Таким образом, параллельно с развитием пись­менности понятие натурального числа принимало всё более отвлечённую фор­му, всё более закреплялось отвлечённое от всякой конкретности понятие числа, воспроизводимого в форме слов в устной речи и в форме обозначения специ­альными знаками в письменной. Важным шагом в развитии понятия натураль­ного числа явилось осознание бесконечности натурального ряда чисел, т. е. по­тенциальной возможности его безграничного продолжения.

Отчётливое представление о бесконечности натурального ряда отражено в памятниках античной математики (3 в. до н. э.), в трудах Евклида и Архимеда. В "Началах" Евклида устанавливается даже безграничная продолжаемость ряда простых чисел, в книге Архимеда "Псаммит" - принципы для построения на­званий и обозначений для сколь угодно больших чисел, в частности больших, чем "число песчинок в мире". [4; 126с]

С развитием понятия натурального числа, как результата счёта предметов в обиход включаются действия над числами. Действия сложения и вычитания возникают сначала как действия над самими совокупностями в форме объеди­нения двух совокупностей в одну и отделения части совокупности. Умножение , по-видимому, возникло в результате счёта равными частями (по два, по три и т.д.), деление - как деление совокупности на равные части. Лишь в многове­ковом опыте сложилось представление об отвлечённом характере этих

действий, о независимости количественного результата действия от природы пред­метов, составляющих совокупности, о том, что, например, два предмета и три предмета составят пять предметов независимо от природы этих предметов. То­гда стали разрабатывать правила действий, изучать их свойства, создавать ме­тоды для решения задач, т. е. начинается развитие науки о числе - арифметики. В первую очередь арифметика развивается как система знаний, имеющая непо­средственно прикладную направленность. [4; 38с]

В процессе развития арифметики проявляется потребность в изучении свойств чисел, как таковых, в уяснении всё более сложных закономерностей в их взаимосвязях, обусловленных наличием действий. Начинается детализация понятия натурального числа, выделяются классы чётных и нечётных чисел, простых и составных и т.д. Изучение глубоких закономерностей в натуральном ряду чисел продолжается и составляет раздел математики, носящий название теория чисел. Натуральные числа, кроме основной функции - характеристики количества предметов, несут ещё другую функцию - характеристику порядка предметов, расположенных в ряд.

Возникающее в связи с этой функцией понятие порядкового числа (пер­вый, второй и т.д.) тесно переплетается с понятием количественного числа (один, два и т.д.). В частности, расположение в ряд считаемых предметов и по­следующий их пересчёт с применением порядковых чисел является наиболее употребительным с незапамятных времён способом счёта предметов (так, если последний из пересчитываемых предметов окажется седьмым, то это и означа­ет, что имеется семь предметов). Вопрос об обосновании понятия натурального числа долгое время в науке не ставился.

Понятие натурального числа столь привычно и просто, что не возникало потребности в его определении в терминах каких-либо более простых понятий. Лишь в середине 19 в. под влиянием развития аксиоматического метода в ма­тематике, с одной стороны, и критического пересмотра основ математического анализа - с другой, назрела необходимость обоснования понятия количествен­ного натурального числа. Отчётливое определение понятия натурального числа

на основе понятия множества (совокупности предметов) было дано в 70-х гг. 19 века в работах Г. Кантора. Сначала он определяет понятие равномощности со­вокупностей. Именно, две совокупности называются равномощными, если со­ставляющие их предметы могут быть сопоставлены по одному. Затем число предметов, составляющих данную совокупность, определяется как то общее, что имеет данная совокупность и всякая другая, равномощная ей совокупность предметов, независимо от всяких качественных особенностей этих предметов. Такое определение отражает сущность натурального числа, как результата счё­та предметов, составляющих данную совокупность. Действительно, на всех ис­торических уровнях счёт заключается в сопоставлении по одному считаемых предметов и предметов, составляющих "эталонную" совокупность (на ранних ступенях - пальцы рук и зарубки на палочке и т.д., на современном этапе - сло­ва и знаки, обозначающие число). Определение, данное Кантором, было от­правным пунктом для обобщения понятия количественных чисел в направле­нии количественной характеристики бесконечных множеств.

Другое обоснование понятия натурального числа базируется на анализе отношения порядка следования, которое, как оказывается, может быть аксио­матизировано. Построенная на этом принципе система аксиом была сформули­рована Дж. Пеано. Следует отметить, что перенесение понятия порядкового числа на бесконечные совокупности резко расходится с обобщённым понятием количественного числа, это обусловлено тем, что количественно одинаковые (равномощные), множества могут быть упорядочены различными способами. Исторически первым расширением понятия числа является присоединение к натуральным числам дробных чисел. Дальнейшие расширения понятия числа обусловлены уже не непосредственными потребностями счёта и измерения, но явились следствием развития математики.

1.3. Содержание курса математики в начальных классах

Содержание начального курса математики определяется целями обуче­ния. С этой точки зрения рассмотрим его важнейшие элементы. Курс математи­ки для младших школьников должен обеспечивать преемственность в изучении математики в средних и старших классах. Это может достигаться по следую­щим направлениям.

1. Некоторые математические знания и умения (с учетом особенностей механизма запоминания, характерных для детей младшего школьного воз­раста) могут быть качественно усвоены именно в начальных классах. Здесь в первую очередь имеются в виду табличные случаи сложения (вычитания), ум­ножения (деления), а также умения, в основе которых лежат несложные алго­ритмы [19; 37с].

Одним из важнейших классов алгоритмизируемых умений являются уст­ные и письменные вычисления. Отработанные в младшем школьном возрасте навыки вычислений на множестве натуральных чисел позволяют учащимся в дальнейшем достаточно легко овладеть более сложными алгоритмами вычис­лений на множестве рациональных и действительных чисел. Поэтому приемы устных и письменных вычислений (сложение, вычитание, умножение и деле­ние) являются естественными элементами программы по математике для на­чальных классов.

2. С некоторыми базовыми математическими понятиями средней
школы учащихся начальных классов можно легко ознакомить на пропедевтиче­
ском уровне, используя житейский опыт учащихся, их наглядно-образные
представления.[10; 64с]

Так, манипулирование множествами хорошо известных учащимся пред­метов служит основой для формирования у них понятия числа, арифметической операции. Наблюдения за окружающим миром дают возможность выделить наиболее часто встречающиеся в действительности формы. Таким образом,

целый ряд геометрических фигур становится предметом изучения в начальной школе.

3. Важным условием полноценного обучения математике является формирование у учащихся навыков математической деятельности.

В методике под термином «математическая деятельность» понимают дея­тельность, сходную по своей сути с математическим познанием. Выделяют три вида математической деятельности, выступающих в органическом единстве: математическую организацию эмпирического материала, логическую организа­цию математического материала, применение математических теорий. [3; 36с]

В начальных классах возможно целенаправленное формирование у уча­щихся навыков математической организации эмпирического материала. Однако при этом учебный материал должен удовлетворять определенным условиям.

Существуют два подхода к формированию математических понятий: ге­нетический и аксиоматический. Аксиоматический подход предполагает, в част­ности, высокий уровень владения учащимися языком, на котором ведется пре­подавание. Естественно, что языковая культура младших школьников только формируется, поэтому аксиоматический подход в начальных классах нереален. [1; 39с.]

Генетический подход заключается в том, что житейские, эмпирические понятия и представления учащихся «переводятся» на язык математики и закре­пляются в форме математических понятий. Такой процесс называется матема­тизацией эмпирического материала (математизацией) и соответствует возмож­ностям младших школьников.

В практике обучения организация деятельности учащихся по математиза­ции и управление ею осуществляются учителем. Однако при рациональной ме­тодике учащиеся в состоянии не только усваивать результаты математизации, но и накапливать опыт ее осуществления. Понятно, что такая методика требует, чтобы вопросы, включенные в программу по математике, имели многочислен­ные (исходя из жизненного опыта детей) интерпретации в реальном мире. Ис­ходя из этих позиций, в программу для начальной школы может быть включен

весьма необычный с точки зрения традиций этой школы математический материал. Примером может служить содержание программы, по которой обучались воспитанники одного из детских садов Бельгии, математический материал для занятий с детьми 6-10 лет, разработанный Р. Ф. Соболевским. [12; 265 с.]

4. Программа по математике должна предусматривать также овладение учащимися математическим языком - средством математизации. Математический язык учащихся начальных классов с синтаксической точки зрения не должен отличатся от языка старшеклассников. Например, предложение o + oo = 3 («к одному яблоку прибавить два яблока...») не является математическим ни для математика, ни для старшеклассника, ни для ученика первого класса. Что же касается смыслового значения математических терминов, знаков, используемых в младших классах, то оно, конечно, беднее соответствующих языковых средств учащихся старших классов, однако не противоречит ему.

Остановимся на более характерных особенностях действующей программы по математике для начальной школы. В содержании программы можно выделить арифметический, геометрический и алгебраический материал, а также материал, связанный с изучением величин. Такое разделение условно, поскольку в младших классах в отличие от средних и старших ни арифметика, ни геометрия, ни алгебра не является систематическими курсами. Соответствующие понятия не образуют строгой логической системы. [18; 53с.]

Рассмотрим особенности арифметического материала. Этот материал занимает в программе центральное место. Целью его изучения является знакомство учащихся с понятием числа - целыми неотрицательными числами и обыкновенными дробями. В средних и старших классах это важнейшее понятие последовательно расширяется. В начальных классах реален первый из названных. Понятие натурального числа вводится

через рассмотрение свойств конечных множеств. Множества служат основой для формирования у учащихся представлений об упорядоченности целых неот­рицательных чисел, арифметических операциях.

Важное место в курсе математики начальных классов занимают законы арифметических операций: коммутативности и ассоциативности сложения и умножения, дистрибутивности умножения относительно сложения.

Арифметический материал изучается концентрически. Поскольку он со­ставляет основу программы по математике, то элементы геометрии и алгебры распределены по соответствующим концентрам. Необходимость знакомства учащихся с понятием числа по концентрам выявляется при логико-дидактическом анализе арифметического материала. В нем можно выделить два основных элемента - нумерацию и арифметические операции.

Рассмотрим сначала логическую последовательность изучения нумерации целых неотрицательных чисел. При этом будем исходить из того, что нумера­ция изучается в десятичной позиционной системе счисления.

1. Нумерация чисел первого десятка (О, 1, ..., 9). Изучается «алфавит»
десятичной системы счисления - написание и название цифр.

2. Нумерация чисел второго десятка (11, 12, ..., 19). Названия этих чисел образуются по особому правилу: 11 - «один-на-дцать», 12 - «две-на-дцать», ..., 19 - «девять-на-дцать». При изучении нумерации используются понятие «десяток» и знания, полученные в концентре 1.

3. Нумерация круглых десятков (20, 30, ..., 90). Названия этих чисел
имеют сходство: «два-дцать», «три-дцать» (вместе с тем «сорок», «девяносто»).
Для их нумерации используются понятие «десяток» и знания, полученные в
концентре 1.

4. Нумерация остальных двузначных чисел (21, 22, ..., 99). Названия
этих чисел образуются из двух слов - сначала называется число десятков, а за­
тем число единиц. Для их нумерации используются знания, полученные в концентрах 1 и З.

Порядок изучения концентров 1, 3, 4 должен строго соблюдаться - снача­ла 1, затем 3, затем 4. Изучать концентры 2 и 3 можно в разной последователь­ности.

5. Нумерация круглых сотен (100, 200, .,., 900), Названия этих чисел
имеют сходство: «сто», «две-сти», «три-ста»,..., «девять-сот».

Для изучения нумерации этих чисел используются понятие «сотня» (раз­ряд сотен) и знания, полученные в концентре 1.

6. Нумерация остальных трехзначных чисел (101, 102, ... 213, ..., 999).
Здесь используются знания, полученные в концентрах 1-5.

7. Нумерация чисел класса тысяч (1000 - 999999). Вводятся понятия
«класс» и «тысяча». Обобщаются знания о разрядах.

Используются знания, полученные во всех предыдущих концентрах.

8. Нумерация чисел свыше 999999. Сообщаются названия новых клас­
сов (миллион, миллиард, триллион и т. д.). Устная и письменная нумерации
этих чисел производятся по уже известным правилам.

Итак, логика изучения нумерации целых неотрицательных чисел опреде­лена. Однако учащиеся должны усваивать нумерацию в органической связи с изучением арифметических операций. Поэтому с методической точки зрения концентры 1-8 далеко не равноценны. В самом деле, при изучении нумерации чисел в пределах десяти, например, учащиеся знакомятся с операцией сложения на множестве чисел первого десятка. Процесс усвоения табличного сложения (в пределах 10) весьма сложный и длительный. Однако знание учащимися табли­цы сложения существенно облегчает изучение операции сложения в концен­трах 3 и 5: эти суммы - 20 + 30, 200 + 300 рассматриваются как 2 дес. + 3 дес, 2 сот. + 3 сот., т. е. как суммы однозначных чисел. Поэтому на изучение нумера­ции круглых десятков и сотен отводятся считанные уроки.

Таким образом, в программе по математике выделяются более крупные концентры, чем 1-8.

Рассмотрим несколько примеров концентрического построения программ по математике для начальной школы.

В дореволюционной программе по математике для начальной школы (ко­нец XIX в.) выделялись три концентра: числа первого десятка, числа первой сотни, многозначные числа. В первом концентре усваивалась нумерация и смысл всех четырех арифметических операций. Запоминались табличные слу­чаи сложения и умножения (вычитания и деления) в пределах десяти. Во вто­ром концентре учащиеся получали знания о нумерации чисел в пределах ста. Здесь же усваивались таблицы сложения и умножения, приемы устного внетабличного сложения и вычитания, умножения и деления в пределах ста. В треть­ем - вместе с нумерацией многозначных чисел (больших ста, меньших милли­арда) изучались приемы письменного сложения, вычитания, умножения (в столбик) и деления (углом).[15; 39с]

В советской послевоенной программе (1945 г.) учебный материал по ма­тематике был распределен по пяти концентрам: числа первого десятка, числа второго десятка, числа в пределах ста, тысячи, многозначные числа. В первом концентре параллельно с нумерацией изучались табличные случаи сложения и соответствующие случаи вычитания в пределах десяти. Во втором концентре завершалось усвоение учащимися таблицы сложения и начиналась работа над таблицей умножения и соответствующими случаями деления в пределах 20. В третьем концентре завершалось изучение таблицы умножения. Отрабатывались приемы устного сложения и вычитания, умножения и деления в пределах ста. В четвертом концентре учащиеся усваивали приемы письменного выполнения всех четырех арифметических действий. В последнем концентре эти приемы отрабатывались при выполнении действий над многозначными числами (до триллиона).[15; 45с]

В программе, утвержденной МП РСФСР в 1968 г., арифметический мате­риал группировался по четырем концентрам: «Десяток», «Сотня», «Тысяча», «Многозначные числа».

В концентре «Десяток» учащиеся усваивали табличные случаи сложения (соответствующие случаи вычитания); в концентре «Сотня» - таблицу сложе­ния в целом, таблицу умножения (соответствующие случаи деления), приемы

устного сложения, вычитания, умножения и деления в пределах ста; в концен­тре «Тысяча» - приемы письменного сложения и вычитания; в концентре «Многозначные числа» - приемы письменного умножения и деления на множе­стве чисел до миллиарда.[15; 46с]

В программе для четырехлетней начальной школы, утвержденной МП РСФСР в 1986 г., по существу выделено пять концентров: числа первого десят­ка, числа второго десятка, числа в пределах ста, числа в пределах тысячи, мно­гозначные числа. [11; 23с]

В первом концентре параллельно с изучением нумерации раскрывается смысл операций сложения и вычитания, учащиеся запоминают таблицу сложе­ния и соответствующие случаи вычитания в пределах десяти. Во втором кон­центре завершается усвоение учащимися таблицы сложения, в третьем — отра­батываются приемы устного сложения и вычитания. Наряду с этим учащиеся должны овладеть приемами письменного выполнения этих действий (в стол­бик). Вычисления в столбик они выполняют в наиболее сложных случаях. Здесь же учащиеся знакомятся с умножением и делением, усваивают таблицу умно­жения, приемы устного внетабличного умножения и деления. При изучении чи­сел в пределах тысячи вводятся приемы письменного умножения (в столбик) и деления (углом). В последнем концентре навыки устных и письменных вычис­лений обобщаются для действий над многозначными числами (до миллиона).

Несмотря на различное построение рассмотренных программ, нумерация в каждой из них изучается в соответствии с выделенной выше последователь­ностью этапов 1-8. Различие программ обусловлено разными позициями авто­ров относительно изучения арифметических операций. Так, составители доре­волюционной программы и программы 1945 г. считали необходимым начинать изучение всех четырех арифметических действий уже в концентре «Десяток»; в программе 1986 г. в отличие от всех предыдущих предусмотрено письменное (в столбик) сложение и вычитание уже на множестве чисел первой сотни. Мы не будем здесь обсуждать достоинства и недостатки рассмотренных программ. Отметим только, что многие вопросы, касающиеся арифметического

содержания программы по математике, еще не нашли в методике полного решения. Таким образом, процесс совершенствования программы по математике для начальных классов продолжается.

Геометрический, алгебраический материал и величины, изучаемые в начальных классах, имеют важное образовательное значение. Однако при включении этого материала в программу по математике исходят из того, что он дол жен быть тесно связан с арифметикой. Например, изучение многоугольников начинается тогда, когда учащиеся знакомятся с числами первого десятка: наряду с различными множествами бытовых предметов для иллюстрации используются геометрические фигуры. Так, число 4 ставится в соответствие множествам, содержащим 4 яблока, 4 автомашины и т. д., и четырехугольнику - фигуре имеющей 4 стороны, 4 вершины, 4 угла. С понятием длины учащиеся знакомятся при изучении темы «Десяток». Линейка при этом используется для иллюстрации упорядоченности натуральных чисел, операций сложения и вычитания Дециметр, например, интерпретируется как десяток (счетная единица), метр - как сотня.

2. МЕТОДИКА ОЗНАКОМЛЕНИЯ МЛАДШИХ ШКОЛЬНИКОВ С НАТУРАЛЬНЫМ ЧИСЛОМ

2.1. Количественные натуральные числа

Огромная роль числа в жизни людей обусловливает довольно раннее формирование числовых представлений у ребёнка. Натуральное число высту­пает для ребёнка на этом этапе как целостный наглядный образ, в котором он ае выделяет единичных предметов. Первые представления детей о числе свя­заны с его количественной характеристикой, и ребёнок может отвечать на вопрос: «Сколько?», не владея операцией счёта.

Количественная характеристика предметных групп осознаётся ребёнком и в процессе установления взаимно-однозначного соответствия между предмет­ными множествами (выражение в понятиях «столько же», «больше», «мень­ше»). Для этого можно использовать: 1) наложение предметов одного множества на предметы другого; (Рис.2)

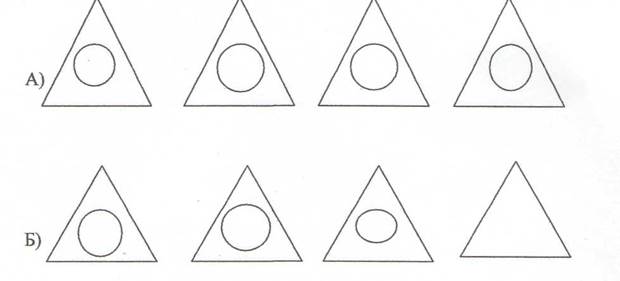
Рис.2 Пример наложения одного множества на предметы другого.

- треугольников столько же, сколько кружков;

- треугольников больше чем кружков;

- кружков, меньше чем треугольников.

2) расположение предметов одного множества под предметами другого; (Рис.3)

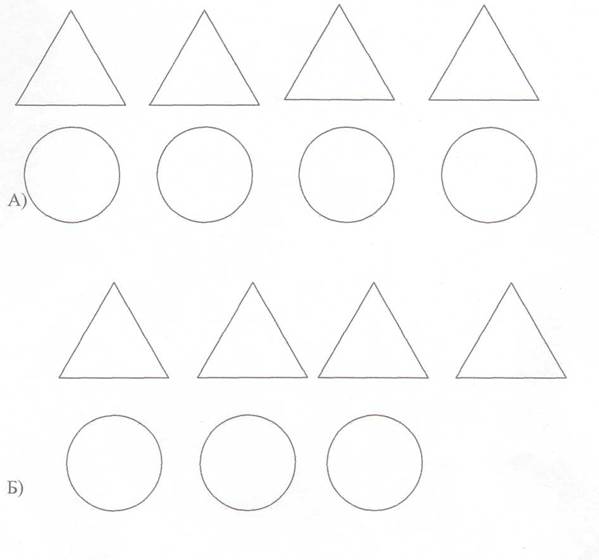
Рис.3 Пример расположения предметов одного множества под предметами дру­гого.

3) соединение каждого предмета одного множества с каждым предметом другого. (Рис. 4)

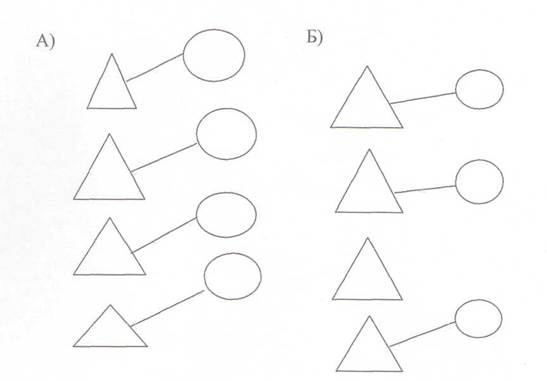
Рис.4 Образование пар.

Установление взаимно-однозначного соответствия между предметными мно­жествами - новый этап в формировании понятия количественного числа, так как он связан с вычленением отдельных элементов и подготавливает детей к операцией счета.

2.2. Взаимосвязь количественных и порядковых чисел. Обучение детей счету

На первом этапе счёт выступает для ребёнка как установление взаимно­однозначного соответствия между предметной совокупностью и совокупно­стью слов-числительных. Для овладения операцией счёта необходимо за­помнить порядок слов-числительных, что закрепляется в результате вы­полнения упражнений типа «Сколько...?» и других упражнений:

1) Что изменилось, не изменилось?

2) Чем похожи, отличаются рисунки?

3) Хватит ли мишкам орехов, если каждому дать по 1; по 2; по 3 ореха?

4) По какому признаку подобраны пары картинок?

5) Покажи «лишнюю» картинку?

Усвоение детьми последовательности слов-числительных позволяет пе­рейти к формированию операции счёта и знакомству учащихся с цифрами. Чтобы учащиеся отличали числа от цифр, полезно познакомить их с другими цифрами (римскими).

Трудно довести до сознания тот факт, что каждое число, названное при счёте, является одновременно и порядковым, т.к. указывает на порядок предмета при счёте. Для осознания взаимосвязи между порядковым и количественным числом можно использовать задания с полоской (это пя­тый кружок, сколько кружков на полоске и т.д.).

Важно, чтобы дети понимали, что, как бы мы ни нумеровали предметы данной совокупности, ответ на вопрос «Сколько?» будет всегда одинаковым, при этом нумерацию надо начинать с 1, не пропускать ни одного предмета и не указывать на один предмет дважды.

Для осознания данного факта можно использовать специальные упражне­ния. В результате таких упражнений дети интуитивно усваивают тот факт, что одному и тому же конечному множеству может соответствовать лишь одно на­туральное число.

2.3. Присчитывание и отсчитывание по одному с использованием отрезка

натурального ряда

Замена слов-числительных, названных в определённой последовательно­сти, цифрами, позволяет познакомить учащихся с отрезком натурального ряда.

В начальных классах, изучение этого понятия сводится к усвоению той закономерности, которая положена в основу построения натурального ряда чисел: каждое число в натуральном ряду больше предшествующего и мень­ше предыдущего на 1.

Теоретико – множественный смысл натуральных чисел,

отношение «меньше».

как было установлено ранее, количественное натуральное число а получается в результате счета элементов конечного множества А: а =n(А). это же число а может быть получено и при пересчете элементов другого множества, например, В. но если а = n(В), то множество А и В равномощны, поскольку содержат поровну элементов.Т.к.любому непустому конечному множеству соответствует только одно натуральное число, то вся совокупность конечных множеств разбивается на классы равномощных множеств. В одном классе будут содержаться все одноэлементные множества, в другом – двухэлементные и т.д. множества одного класса различны по своей природе, но все они содержат одинаковое число элементов. И это число можно рассматривать как общее свойство класса конечных равномощных множеств.Т.о, с теоретико-множественной точки зрения, натуральное число – общее свойство класса конечных равномощных множеств.

Свойства отношения «меньше» для натуральных чисел также получают теоретико-множественное истолкование: транзитивности и антисимметричность этого отношения связаны с тем, что транзитивно и антисимметрично отношение «быть подмножеством».

Теоретико-множественный смысл 0<а истинного для любого натурального числа а, связан с тем, что пустое множество является подмножеством отрезка N_а (или любого такого множества А, для которого а=n(A)).