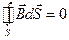Число уравнений, составляемых по первому закону Кирхгофа, должно быть на единицу меньше числа узлов, содержащихся в цепи.
4. При составлении уравнений по второму правилу Кирхгофа следует считать:
а) падение напряжения на участке цепи (т.е. произведение 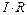 ) входит в уравнение со знаком плюс, если направление тока в данном участке совпадает с выбранным направлением обхода контура; в противном случае произведение
) входит в уравнение со знаком плюс, если направление тока в данном участке совпадает с выбранным направлением обхода контура; в противном случае произведение 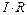 входит в уравнение со знаком минус;
входит в уравнение со знаком минус;
б) ЭДС 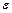 входит в уравнение со знаком плюс, если оно повышает потенциал в направлении обхода контура: т.е. если при обходе контура внутри источника тока приходится идти от минуса к плюсу, в противном случае ЭДС
входит в уравнение со знаком плюс, если оно повышает потенциал в направлении обхода контура: т.е. если при обходе контура внутри источника тока приходится идти от минуса к плюсу, в противном случае ЭДС 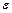 входит в уравнение со знаком минус.
входит в уравнение со знаком минус.
Число независимых уравнений, которые могут быть составлены по второму закону Кирхгофа, равно числу независимых контуров, имеющихся в цепи.
Для составления уравнений первый контур можно выбрать произвольно. Все следующие контуры следует выбирать таким образом, чтобы в каждый новый контур входила хотя бы одна ветвь цепи, не участвовавшая ни в одном из ранее использованных контуров. Произвольно выбранное направление обхода по контурам не изменяется до конца решения задачи.
Если при решении уравнений, составленных вышеуказанным способом, получены отрицательные значения силы тока или напряжения, то это означает, что ток через данное сопротивление в действительности течет в направлении, противоположном выбранному.
ПЕРЕМЕННЫЙ ТОК
Эффективное (или действующее) значение силы тока и напряжения 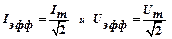
Закон Ома для цепи переменного тока только с активным сопротивлением 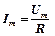
Закон Ома для цепи переменного тока с идеальной индуктивность 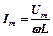
Индуктивное сопротивление 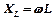
Закон Ома для цепи переменного тока с идеальной ёмкостью 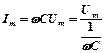
Емкостное сопротивление 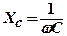
Закон Ома для цепи переменного тока с последовательно соединёнными 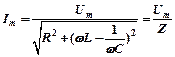
активным сопротивлением, ёмкостью и индуктивностью
Полное сопротивление (или импеданс) цепи переменного тока 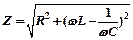
Сдвиг фаз между силой тока и напряжением в цепи переменного тока 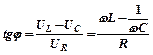
ЭЛЕКТРОМАГНЕТИЗМ
Уравнения Максвелла в интегральной форме (или полевые уравнения Максвелла)
Первое уравнение 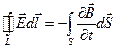
Второе уравнение 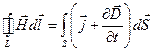
Третье уравнение 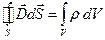
Четвёртое уравнение