Схема решения задач на взаимодействие однородного магнитного поля с проводником или контуром с током или
с движущимися заряженными частицами
1. сделать схематический чертёж, указав на нём проводник с током, контур с током или движущуюся заряженную частицу,
2. показать направление силовых линий магнитного поля, отметив углы между направлением вектора магнитной индукции и проводником, отдельными элементами контура или вектором начальной скорости частицы и указать заряд частицы.
3. Записать формулы для определения силы Ампера, магнитного вращательного момента силы или силы Лоренца. Если этого оказывается достаточно, то дорешать задачу.
4. Если этого недостаточно, то возможно это задача на динамику или статику. В этом случае определить и нарисовать все силы, действующие на проводник с током, контур с током или частицу, записать уравнение динамики и решить его. При необходимости использовать дополнительно уравнения кинематики или законы сохранения или изменения.
5. Если понадобится использовать законы сохранения или изменения, то выполняют пункт 2 для моментов времени, о которых есть информация в задаче, записывают законы сохранения или изменения импульса или полной механической энергии и решают полученную систему уравнений.
Схема решения задач о явлении электромагнитной индукции и самоиндукции
1. сделать схематический чертёж, указав на нём контур с током,
2. показать направление силовых линий магнитного поля, отметив углы между направлением вектора магнитной индукции и нормалью к плоскости контура,
3. Записать закон Фарадея. При этом следует установить, за счёт чего изменяется величина магнитного потока: за счёт изменения магнитной индукции, за счёт изменения площади контура или за счёт изменения ориентации контура в магнитном поле. При необходимости добавляют уравнения связи площади контура с его геометрическими размерами и решают полученную систему уравнений.
СХЕМА РЕШЕНИЯ ЗАДАЧ НА ПРИМЕНЕНИЕ ЗАКОНОВ ГИДРОСТАТИКИ
1. сделать рисунки, на которых показать все равновесные уровни жидкости, которые она занимала в разных состояниях и изобразить границы раздела различных жидкостей,
2. выбрать нулевой горизонтальный уровень отсчёта высот столбов различных жидкостей. (обычно его выбирают так, чтобы он проходил по нижней границе раздела сред,
3. записать условие равновесия жидкости, где и суммарное давление внутри жидкости в точках и , располпженных на одном горизонтальном уровне в покоящейся жидкости,
4. если до установления равновесия происходило переливания жидкости из одной части в другую, то к условию равновесия следует добавить условие не сжимаемости жидкости , где -уменьшение объёма жидкости в одной части сосуда, а - увеличение его в другой части сосуда,
5. решить полученную систему уравнений.
Формулы и законы, которые могут Вам понадобиться при решении РГЗ
КИНЕМАТИКА
Положение материальной точки в пространстве задается радиусом-вектором г: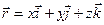 
, 
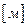
где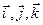 
— единичные векторы направлений (орты); х, у, z — координаты точки.
Мгновенная скорость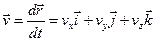 
, 
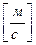
где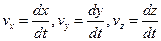 
— проекции скорости v на оси координат.
Модуль скорости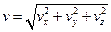 
Мгновенное ускорение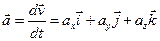 
, 
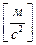
где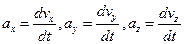 
- проекции ускорения a на оси координат.
Модуль ускорения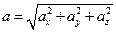 
Уравнения поступательного движения:
; 
;
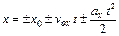
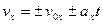
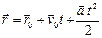
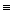
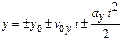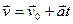
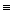
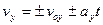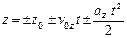
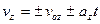
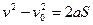- если движение равноускоренное,
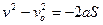- если движение равнозамедленное.
Угловая скорость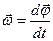 
, 
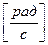
Угловое ускорение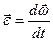 
, 
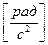
Полное ускорение материальной точки при криволинейном движении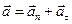 
Модуль полного ускорение материальной точки при криволинейном движении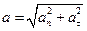 
Уравнения вращательного движения: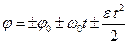 
, 
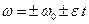
Связь линейных и угловых величин:
; 
; 
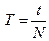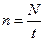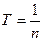; ω =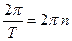 
; 
; 
; 
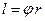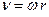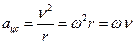
Кинематика сложного движения:
; 
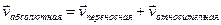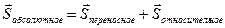
Кинематика относительного движения: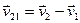 
; 
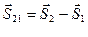
средняя скорость по перемещению: средняя путевая скорость
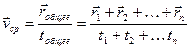
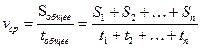
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
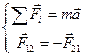
Законы Ньютона:
- сила гравитации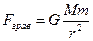 
- сила тяжести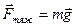 
- сила упругости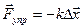 
жесткость системы пружин при их последовательном соединении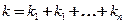 
жесткость системы пружин при их параллельном соединении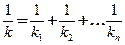 
- сила трения скольжения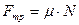 
- сила Архимеда 