7.29. Объяснить, почему волновая функция должна быть конечной, однозначной и непрерывной.

Дата: 2025-06-14; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

7.30. Записать выражение для вероятности W обнаружения частицы в конечном объеме V, если известна координатная пси-функция частицы ψ(x, y, z).

7.31. Известно, что свободная квантовая частица описывается плоской монохроматической волной де Бройля. Плотность вероятности (вероятность, отнесенная к единице объема) обнаружения свободной частицы |ψ|2 = ψψ* = |А|2 = const. Объяснить, что означает постоянство этой величины.

7.32. Записать уравнение Шредингера для стационарных состояний для свободной частицы, движущейся вдоль оси х, а также определить посредством его решения собственные значения энергии. Что можно сказать об энергетическом спектре свободной частицы? Ответ: E = ħ2.k2 / (2m).

7.33. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками» находится в основном состоянии. Определить вероятность обнаружения частицы в левой трети «ямы». Ответ: 0,195.

7.34. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками» находится в возбужденном состоянии (n = 2). Определить вероятность обнаружения частицы в области 3/8 l ≤ х ≤ 5/8 l . Ответ: 0,091.

7.35. Электрон находится в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками». Определить вероятность W обнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии (n = 3). Пояснить физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии. Ответ: 1/3.

7.36. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками» находится в возбужденном состоянии (n = 3). Определить, в каких точках «ямы» (0 ≤ х ≤ 1) плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Пояснить полученный результат графически. Ответ: 1) l/6, l/2, 5l/6; 2) l/3, 2l/3.

7.37. Определить, при какой ширине одномерной прямоугольной «потенциальной ямы» с бесконечно высокими «стенками» дискретность энергетического спектра электрона сравнима с его средней кинетической энергией при температуре Т. Ответ: l = ħ.π / .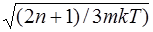

7.38. Доказать, что энергия свободных электронов в металле не квантуется. Принять, что ширина l прямоугольной «потенциальной ямы» с бесконечно высокими «стенками» для электрона в металле составляет 10 см. Ответ: ΔE≈ 0,75n.10-16 эВ.

7.39. Частица находится в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Определить, во сколько раз изменяется отношение разности соседних энергетических уровней частицы: 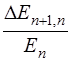при переходе от n = 3 к n ' = 8. Объяснить физическую сущность полученного результата. Ответ: Уменьшается в 3 раза.

7.40. Частица с энергией E движется в положительном направлении оси x и встречает на своем пути прямоугольный потенциальный барьер высотой U и конечной шириной l, причем E < U. Записать уравнение Шредингера для областей 1, 2 и 3.

7.41. Электрон с энергией Е = 4 эВ движется в положительном направлении оси х, встречая на своем пути прямоугольный потенциальный барьер высотой U = 10 эВ и шириной l = 0,1 нм. Определить коэффициент D прозрачности потенциального барьера. Ответ: 0,1.

7.42. Прямоугольный потенциальный барьер имеет ширину l = 0,1 нм. Определить в электрон-вольтах разность энергий (U – E ), при которой вероятность прохождения электрона сквозь барьер составит 0,5. Ответ: 0,454 эВ.

7.43. Протон с энергией Е = 5 эВ движется в положительном направлении оси х, встречая на своем пути прямоугольный потенциальный барьер высотой U = 10 эВ и шириной l = 0,1 нм. Определить: 1) вероятность прохождения протоном этого барьера; 2) во сколько раз надо сузить барьер, чтобы вероятность прохождения его протоном была такой же, как для электрона при вышеприведенных условиях. Ответ: 1) 1,67.10-43; 2) в 42,9 раза.

7.44. Прямоугольный потенциальный барьер имеет ширину l = 0,1 нм. Разность между высотой потенциального барьера и энергией движущегося в положительном направлении оси х электрона U – E = 5 эВ. Определить, во сколько раз изменится коэффициент D прозрачности потенциального барьера для электрона, если разность U – E возрастет в 4 раза. Ответ: Уменьшится в 10 раз.

7.45. Электрон с длиной волны де Бройля λ1 = 100 нм, двигаясь в положительном направлении оси х, встречает на своем пути бесконечно широкий прямоугольный барьер высотой U = 100 эВ. Определить длину волны де Бройля после прохождения барьера. Ответ: λ2 = λ1 / 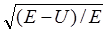= 172 пм.

7.46. Частица с энергией Е = 50 эВ, двигаясь в положительном направлении оси х, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 20 эВ. Определить вероятность отражения электрона от этого барьера. Ответ: W = 0,016.

7.47. Частица массой m = 10-19 кг, двигаясь в положительном направлении оси х со скоростью υ = 20 м/с, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 100 эВ. Определить коэффициент отражения R волн де Бройля на границе потенциального барьера. Ответ: R = 0,146.

7.48. Электрон с длиной волны λ де Бройля, равной 120 пм, движется в положительном направлении оси x и встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 200 эВ. Определить коэффициент отражения R волн де Бройля на границе потенциального барьера. Ответ: R = l.

7.49. Объяснить физический смысл существования энергии нулевых колебаний для квантового гармонического осциллятора. Зависит ли наличие нулевых колебаний от формы «потенциальной ямы»?

7.50. Математический маятник можно рассматривать в качестве гармонического осциллятора. Определить в электрон-вольтах энергию нулевых колебаний для маятника длиной l = 1 м, находящегося в поле тяготения Земли. Ответ: 1,03.10-15 эВ.

7.51. Рассматривая математический маятник массой m = 100 г и длиной l = 0,5м в виде гармонического осциллятора, определить классическую амплитуду А маятника, соответствующую энергии нулевых колебаний этого маятника. Ответ: А = 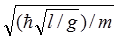= 1,54.10-17 м.

 

8. Элементы современной физики атомов и молекул

8.1. Представить: 1) уравнение Шредингера для стационарных состояний электрона, находящегося в атоме водорода; 2) собственные значения энергии, удовлетворяющие уравнению; 3) график потенциальной энергии взаимодействия электрона с ядром; 4) возможные дискретные значения энергии на этом графике.

8.2. Как известно, уравнению Шредингера, описывающему атом водорода, удовлетворяют собственные функции ψnlm,(r, Θ, φ), определяемые тремя квантовыми числами: главным n, орбитальным l и магнитным ml. Объяснить физический смысл указанных квантовых чисел к записать их возможные значения.

8.3. Волновая функция ψnlm,(r, Θ, φ), описывающая атом водорода, определяется главным квантовым числом n, орбитальным квантовым числом l и магнитным квантовым числом ml. Определить, чему равно число различных состояний, соответствующих данному n. Ответ: n2.

8.4. Записать возможные значения орбитального квантового числа l и магнитного квантового числа ml для главного квантового числа n = 4.

8.5. Определить, сколько различных волновых функций соответствует главному квантовому числу n = 3.

8.6. Учитывая число возможных состояний, соответствующих данному главному квантовому числу n, а также правила отбора, представить на энергетической диаграмме спектральные линии атома водорода, образующие серии Лаймана и Бальмера.

8.7. Показать возможные энергетические уровни атома с электроном в состоянии с главным квантовым числом n = 6, если атом помещен во внешнее магнитное поле.

8.8. Построить и объяснить диаграмму, иллюстрирующую расщепление энергетических уровней и спектральных линий (с учетом правил отбора) при переходах между состояниями l = 2 и l = 1. Ответ: d - p-переход.

8.9. Построить и объяснить диаграмму, иллюстрирующую расщепление энергетических уровней и спектральных линий при переходах между состояниями с l = 1 и l = 0. Ответ: р- s-переход.

8.10. Электрон в атоме находится в f-состоянии. Определить возможные значения (в единицах h) проекции момента импульса Lz орбитального движения электрона в атоме на направление внешнего магнитного поля.

8.11. Электрон в атоме находится в d-состоянии. Определить: 1) момент импульса (орбитальный) L электрона; 2) максимальное значение проекции момента импульса (Lz)max на направление внешнего магнитного поля. Ответ: 1) 2,45ħ; 2) 2ħ.

8.12. Определить, во сколько раз орбитальный момент импульса L электрона, находящегося в f-состоянии, больше, чем для электрона в р-состоянии. Ответ: В 2,45 раза.

8.13. 1-s электрон атома водорода, поглотив фотон с энергией E = 12,1 эВ, перешел в возбужденное состояние с максимально возможным орбитальным квантовым числом. Определить изменение момента импульса ΔL орбитального движения электрона. Ответ: 2,57.10-34 Дж.с.

8.14. Объяснить, почему в опыте Штерна и Герлаха по обнаружению собственного механического момента импульса (спина) электрона использовался пучок атомов водорода, заведомо находящихся в s-состоянии.

8.15. Объяснить, почему в опыте Штерна и Герлаха по обнаружению собственного механического момента импульса (спина) электрона использовалось неоднородное магнитное поле.

8.16. Определить числовое значение: 1) собственного механического момента импульса (спина) Ls; 2) проекцию спина Lsz на направление внешнего магнитного поля. Ответ:1)9,09.10-35Дж.с; 2) 5,25.10-35 Дж.с.

8.17. Объяснить, что лежит в основе классификации частиц на фермионы и бозоны, а также которые из них описываются симметричными волновыми функциями.

8.18. Исходя из принципа неразличимости тождественных частиц, дать определение симметричной и антисимметричной волновых функций. Объяснить, почему изменение знака волновой функции не влечет за собой изменение состояния.

8.19. Учитывая принцип Паули, определить максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом.

8.20. Заполненной электронной оболочке соответствует главное квантовое число n = 3. Определить число электронов в этой оболочке, которые имеют одинаковые следующие квантовые числа: 1) ms = -1/2; 2) m = 0. Ответ:1)9; 2)6.

8.21. Заполненной электронной оболочке соответствует главное квантовое число n = 4. Определить число электронов в этой оболочке, которые имеют одинаковые следующие квантовые числа: 1) m = -3; 2) ms = 1/2, l = 2; 3) т s = -1/2, т l = 1. Ответ:1) 2; 2) 5; 3) 3.

8.22. Определить суммарное максимальное число s-, p-, d-, f- и g-электронов, которые могут находиться в N- и 0-оболочках атома. Ответ: 82.

8.23. Записать квантовые числа, определяющие внешний, или валентный, электрон в основном состоянии атома натрия.

8.24. Пользуясь Периодической системой элементов Д.И. Менделеева, записать символически электронную конфигурацию следующих атомов в основном состоянии: 1) неона; 2) аргона; 3) криптона.

8.25. Пользуясь Периодической системой элементов Д.И. Менделеева, записать символически электронную конфигурацию атома меди в основном состоянии.

8.26. Пользуясь Периодической системой элементов Д.И. Менделеева, записать символически электронную конфигурацию атома цезия в основном состоянии.

8.27. Электронная конфигурация некоторого элемента 1s22s22p63s23p. Определить, что это за элемент.

8.28. Электронная конфигурация некоторого элемента 1s22s22p63s23p64s. Определить, что это за элемент.

8.29. Определить в Периодической системе элементов Д.И. Менделеева порядковый номер элемента, у которого в основном состоянии заполнены К, L, М-оболочки, а также 4s- подоболочка.

8.30. Объяснить: 1) почему тормозной рентгеновский спектр является сплошным; 2) почему сплошной рентгеновский спектр имеет резкую границу со стороны коротких волн и чем определяется ее положение.

8.31. Определить наименьшую длину волны рентгеновского излучения, если рентгеновская трубка работает при напряжении U = 150 кВ. Ответ: 8,29 пм.

8.32. Минимальная длина волны рентгеновских лучей, полученных от трубки, работающей при напряжении U = 60 кВ, равна 20,7 нм. Определить по этим данным постоянную Планка. Ответ: 6,62.10-34 Дж.с.

8.33. Определить длину волны коротковолновой границы сплошного рентгеновского спектра, если скорость υ электронов, бомбарди­рующих анод рентгеновской трубки, составляет 0,8 с. Ответ: 3,64 пм.

8.34. Определить длину волны коротковолновой границы сплошного рентгеновского спектра, если при увеличении напряжения на рентгеновской трубке в два раза она изменилась на 50 пм. Ответ: 100 пм.

8.35. Определить порядковый номер элемента в Периодической системе элементов Д. И. Менделеева, если граничная частота К-серии характеристического рентгеновского излучения составляет 5,55.1018 Гц. Ответ: 42, молибден.

8.36. Определить порядковый номер элемента в Периодической системе элементов Д. И. Менделеева, если длина волны λ линии К2 характеристического рентгеновского излучения составляет 72 пм. Ответ: 42, молибден.

8.37. Определить длину волны самой длинноволновой линии К-серии характеристического рентгеновского спектра, если анод рентгеновской трубки изготовлен из платины. Постоянную экранирования принять равной единице. Ответ: 20,4 пм.

8.38. Определить постоянную экранирования b для L-серии рентге­новского излучения, если при переходе электрона в атоме вольфрама с М-оболочки на L-оболочку длина волны λ испущенного фотона составляет 140 пм. Ответ: 5,63.

8.39. В атоме вольфрама электрон перешел с М-оболочки на L-оболочку. Принимая постоянную экранирования b = 5,63, определить энергию испущенного фотона. Ответ: 8,88 кэВ.

8.40. Известно, что в спектре комбинационного рассеяния помимо несмещенной спектральной линии возникают стоксовы (или красные) и антистоксовы (или фиолетовые) спутники. Объяснить механизм их возникновения и их свойства.

8.41. Объяснить механизм возникновения, свойства и особенности вынужденного (индуцированного) излучения.