7.10. Вывести связь между длиной круговой электронной орбиты и длиной волны де Бройля.
7.11. Определить, как изменится длина волны де Бройля электрона атома водорода при переходе его с четвертой боровской орбиты на вторую. Ответ: Уменьшится в 2 раза.
7.12. В опыте Дэвиссона и Джермера, обнаруживших дифракционную картину при отражении пучка электронов от естественной дифракционной решетки – монокристалла никеля, оказалось, что в направлении, составляющем угол α = 55° с направлением падающих электронов, наблюдается максимум отражения четвертого порядка при кинетической энергии электронов Т = 180 эВ. Определить расстояние между кристаллографическими плоскостями никеля. Ответ: d = h.k / (2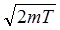 
cos(α/2)) = 0,206 нм, k – порядок максимума.
7.13. Моноэнергетический пучок нейтронов, получаемый в результате ядерной реакции, падает на кристалл с периодом d = 0,15 мм. Определить скорость нейтронов, если брэгговское отражение первого порядка наблюдается, когда угол скольжения Θ = 30°. Ответ: 2,64 км/с.
7.14. Параллельный пучок моноэнергетических электронов направлен нормально на узкую щель шириной а = 1 мкм. Определить скорость этих электронов, если на экране, отстоящем на расстоянии l = 20 см от щели, ширина центрального дифракционного максимума составляет Δx = 48 мкм. Ответ: υ = 2hl / (am.Δx) = 606 км/с.
7.15. Параллельный пучок электронов, ускоренный разностью потенциалов U = 50 В, направлен нормально на две параллельные, лежащие в одной плоскости, щели, расстояние d между которыми равно 10 мкм. Определить расстояние между центральным и первым максимумами дифракционной картины на экране, который расположен от щелей на расстоянии l = 0,6 м. Ответ: Δx = 2hl / (d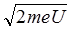 
) = 10,4 мкм.
7.16. Объяснить, почему представление о боровских орбитах несовместимо с принципом неопределенности.
7.17. Ширина следа электрона (обладающего кинетической энергией Т = 1,5 кэВ) на фотопластинке, полученного с помощью камеры Вильсона, составляет Δx = 1 мкм. Определить, можно ли по данному следу обнаружить отклонение в движении электрона от законов классической механики. Ответ: Δpx/px = 10-4, нет.
7.18. Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U = 1 кВ. Известно, что неопределенность скорости составляет 0,1 % от ее числового значения. Определить неопределенность координаты электрона. Являются ли электроны в данных условиях квантовыми или классическими частицами? Ответ: Δx = 38,8 нм.
7.19. Определить отношение неопределенностей скорости электрона, если его координата установлена с точностью до 10-5 м, и пылинки массой m = 10-12 кг, если ее координата установлена с такой же точностью. Ответ: 1,1·1018.
7.20. Электронный пучок выходит из электронной пушки под действием разности потенциалов U = 200 В. Определить, можно ли одновременно измерить траекторию электрона с точностью до 100 нм (с точностью порядка диаметра атома) и его скорость с точностью до 10 %. Ответ: m.Δυ.Δx < h; нет.
7.21. Электрон движется в атоме водорода по первой боровской орбите. Принимая, что допускаемая неопределенность скорости составляет 10 % от ее числового значения, определить неопределенность координаты электрона. Применимо ли в данном случае для электрона понятие траектории? Ответ: Δx = 3,34 нм, нет.
7.22. Применяя соотношение неопределенностей, показать, что для движущейся частицы, неопределенность координаты которой равна длине волны де Бройля, неопределенность скорости равна по порядку величины самой скорости частицы.
7.23. Используя соотношение неопределенностей в форме Δpx.Δx ≥ ħ, оценить минимально возможную полную энергию электрона в атоме водорода. Принять неопределенность координаты равной радиусу атома. Сравнить полученный результат с теорией Бора. Ответ: Emax = –me4 / (8h2.ε02) = -13,6 эВ.
7.24. Объяснить физический смысл соотношения неопределенности для энергии E и времени t: ΔE.Δt ≥ h .
7.25. Воспользовавшись соотношением неопределенностей, оценить размытость энергетического уровня в атоме водорода: 1) для основного состояния; 2) для возбужденного состояния (время его жизни равно 10-8с). Ответ: 1) 0; 2) 414 нэВ.
7.26. Длина волны λ излучаемого атомом фотона составляет 0,6 мкм. Принимая время жизни возбужденного состояния Δt = 10-8 c, определить отношение естественной ширины энергетического уровня, на который был возбужден электрон, к энергии, излученной атомом. Ответ: ΔЕ/Е = λ / (c.Δt) = 2.10-7.
7.27. Принимая, что электрон находится внутри атома диаметром 0,3 нм, определить (в электрон-вольтах) неопределенность энергии этого электрона. Ответ: ΔЕ = h 2 / 2m. (Δx)2 = 16,7 эВ.
7.28. Объяснить, почему физический смысл имеет не сама ψ-функция, а квадрат ее модуля |ψ|2.