3 Метод контурных токов
Практическое занятие 3
3 Метод контурных токов
3.1 Основные теоретические сведения
Универсальными законами, позволяющими рассчитать любую электрическую цепь, являются законы Кирхгофа. Для упрощения математических расчетов, уменьшения порядка системы линейных алгебраических уравнений, Максвеллом были предложены методы контурных токов и узловых потенциалов.
Метод контурных токов (метод Максвелла) заключается в том, что вводятся в рассмотрение расчётные, реально не существующие, "контурные токи", которые как бы протекают в произвольном контуре сложной электрической цепи. Если рассматриваемая цепь содержит источники тока, то токи этих источников принимают за известные "контурные токи", замыкающиеся по некоторому контуру. Реально существующие токи в ветвях определяют через вышеуказанные "контурные токи" путем алгебраического суммирования этих токов.
Количество уравнений по методу контурных токов совпадает с количеством независимых уравнений, составляемых по второму закону Кирхгофа, и оно может быть определено по формуле (5).
В общем случае эта система уравнений имеет следующий вид:
R11·Ij+R12·Ik+…+R1n·I(n)+R1,I1·I1+R1,I2·I2+…+R1,Im·Im = Ej
R21·Ij+R22·Ik+…+R2n·I(n)+R2,I1·I1+R2,I2·I2+…+R2,Im·Im = Ek
...............................……….…………………………………………………..……………………………………………. (6)
Ri1·Ij+Ri2·Ik+…+Ri,n·I(n)+Ri,I1·I 1+Ri,I2·I2+…+Ri,Im·Im = E(i)
……………………………………………………………………………………………………………………………
Rn1·Ij+ Rn2·Ik+…+ Rn,n·I(n)+ Rn,I1·I1+ Rn,I2·I2+…+Rn,Im·Im = E(n)
где n – количество контурных токов;
m – количество источников тока;
I( j ) – “j ”-ый контурный ток (j = 1,2,3,…, n), А;
Ik – ток “к”-го источника тока (к = 1,2,…,m), А;
Rij , Ri , Ik – расчетные сопротивления (i =1 ,2,...,n;), Ом;
E ( i ) – “i ”-ая контурная э.д.с. (i=1,2,...,n), В.
Условные положительные направления контурных токов могут выбираться произвольно.
Расчётные сопротивления Rij могут быть двух типов.
Если эти сопротивления имеют одинаковые индексы, т.е. если i = j, то они называются «собственными» сопро-тивлениями контуров. «Собственные» сопротивления кон-туров вычисляются, как сумма всех сопротивлений, входя-щих в рассматриваемы контур.
Если расчетные сопротивления имеют разные индексы, т.е. i ≠ j, то Rij = Rji и они называются «взаимными» сопротивлениями контуров. Эти сопротивления равны сопротивлению ветви, являющейся общей для “i”-го и “j”-го контуров. Причём, если направления контурных токов в рассматриваемой ветви совпадают, то взаимное сопро-тивление принимается положительным, а в противном случае - отрицательным. Если условные положительные направления всех контурных токов принимать одина-ковыми (по часовой стрелке или против часовой стрелки), то взаимные сопротивления контуров всегда будут отрицательными. Сопротивления Ri , Ik представляют собой взаимные сопротивления “i”-го контура с “к”-ым током источника тока Ik , который принимается в качестве извест-ного контурного тока, и эти сопротивления вычисляются по вышеуказанному правилу.
Контурные э.д.с. Е( i ) также представляют собой некоторые расчётные э.д.с., равные алгебраической сумме э.д.с. в ветвях, обтекаемых контурным током I( j ). Если направление э.д.с. Ek совпадает с направлением контурного тока, то при суммировании соответствующая э.д.с. входит со знаком “+”, а в противном случае - со знаком “ – ”.
Решение системы (6) позволяет определить все контурные токи. Реально существующие токи в ветвях схе-мы вычисляются путём алгебраического суммирования контурных токов, протекающих по данной ветви. При этом контурный ток, направление которого совпадает с выбран-ным положительным направлением тока в ветви, принимается со знаком “+ ”, а в противном случае – со знаком “ – ”. Если же в некоторой ветви протекает лишь один контурный ток, то ток в этой ветви равен контурному току, взятому со знаком “ + ”, если условные положительные направления тока ветви и контурного тока одинаковые, а в противном случае – со знаком “ – ”.
Дадим обоснование указанного метода.
Любая разветвленная электрическая цепь состоит из нескольких смежных контуров. Например, в электрической цепи рис. 1 таких контуров три: абвга, бдвб и абдеа.
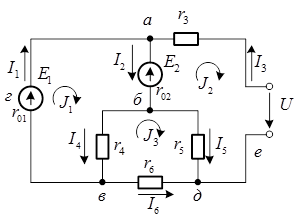
Рис. 1. К пояснению метода контурных токов
Каждый контур имеет несмежные ветви, принадлежащие лишь данному контуру, и смежные ветви, при принадлежащие также соседним контурам. Так, контур абвга имеет несмежную ветвь вга и две смежные ветви аб и бв.
Допустим, что в каждом контуре рис. 1 имеется некоторый контурный ток, одинаковый для всех элементов контура. На рис. 1 контурные токи обозначены J1, J2 и J3. Положительные направления контурных токов могут быть выбраны произвольно. Наложим на контурные токи следующее условие: контурные токи должны быть равны по абсолютному значению токам несмежных ветвей соответствующих контуров.
Если удастся найти контурные токи, то через них легко определить и токи всех ветвей. В силу наложенного условия токи несмежных ветвей следует определять так: если выбрать положительное направление тока несмежной ветви совпадающим с контурным током, то ток ветви должен быть равен контурному току; если же направить ток несмежной ветви против контурного тока, то он должен быть равен контурному току со знаком «̶». Так, токи в несмежных ветвях цепи (рис. 1) будут равны
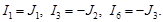
Чтобы выяснить, как определять токи смежных ветвей, выразим ток в узле а через токи I1, I2 и I3 и заменим последние контурными токами:
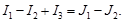
Аналогично найдем
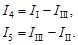
Как видно, со знаком « + » должен быть взят тoт контурный ток, направление которого совпадает с направлением тока смежной ветви; контурный току направленный в противоположную сторону, должен быть взят со знаком «̶ ».
Нетрудно доказать, что контурные токи могут быть определены путем совместного решения системы уравнений, составленных по второму закону Кирхгофа, в которые вместо падения напряжения oi токов ветвей следует ввести падения напряжения от контурных токов с соответствующими знаками.
Уравнение по второму закону Кирхгофа при включении в него контурных токов в общем случае имеет вид
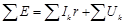
Для рассматриваемой цепи (рис. 1) уравнения будут:
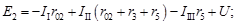
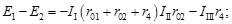
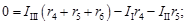
При решении задач рассмотренным методом целесообразно выбирать положительные направления токов ветвей после определении контурных токов. В этом случае можно выбрать положительные направления токов ветвей так, чтобы все они совпадали с их действительными направлениями.
Алгоритмом метода контурных токов:
1. Задаются направлением токов ветвей и обозначают их на схеме.
2. Определяют независимые контуры и их нумеруют. При наличии в схеме источников тока независимые контуры, для которых составляются уравнения метода контурных токов, можно определить, если мысленно удалить источники тока.
3. Выбирают направление контурных токов (целесообразно в одну сторону) и составляют уравнения по методу контурных токов, обходя каждый контур в направлении его контурного тока. Контурный ток, проходящий через источник тока, известен и равен току источника тока (через источник тока проходит только один контурный ток!).
4. Полученную систему алгебраических уравнений решают относительно неизвестных контурных токов.
5. Искомые токи по методу контурных токов находят как алгебраическую сумму контурных токов, проходящих по данной ветви. Токи в ветвях связи равны контурным токам.
3.2. Примеры решения
Задача 1. Методом контурных токов определить токи в ветвях схемы (рисунок 1) если Е1=145 В, Е2=140 В, R1=R2=R6=1 Ом, R3=0.5 Ом, R4=10 Ом, R5=4 Ом, R7=8 Ом, R8=5 Ом.
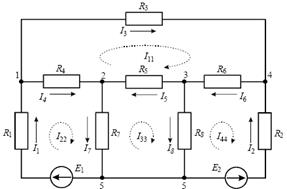
Рис. 1
Решение:
Определяем количество уравнений системы:
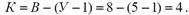
Выбираем контуры и записываем для каждого контура
уравнения по второму закону Кирхгофа:
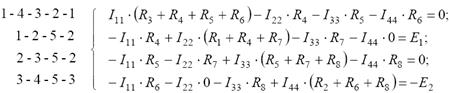
Решив систему одним из численных методов, получим значения контурных токов:
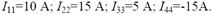
Затем выражаем токи ветвей из контурных токов:
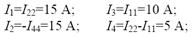
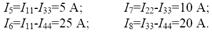
Составляем баланс мощностей:
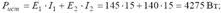
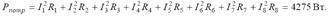
Задача 1.1.2 Методом контурных токов определить токи в ветвях схемы (рисунок 2), если Е1=30 В, Е2=Е5=10 В, J=7 A, R1=R3=R4=10 Ом, R2=R5=5 Ом.
Решение:
Определяем количество уравнений системы:
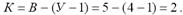
Первый независимый контур выбираем так, чтобы он был образован ветвью с идеальным источником тока J, и контурный ток данного контура считаем равным току источника тока I11 = J, остальные контуры выбираем так, чтобы ветвь с источником тока не являлась образующей (рисунок 2).
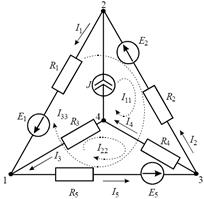
Рис. 2
Запишем систему уравнений:
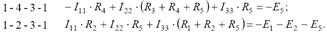
Так как ток первого контура известен, то его произведение на взаимное сопротивление контуров можно перенести в правую часть уравнения, и система уравнений будет иметь следующий вид:
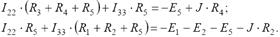
Решив систему уравнений, получим значения контурных токов: 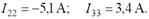
Методом наложения определяем токи в ветвях схемы:
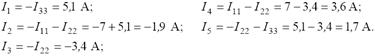
Составляем уравнение баланса мощностей:
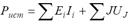
где UJ - напряжение на зажимах источника тока.
Для схемы рисунка 2 напряжение UJ выразим из уравнения, записанного по II закону Кирхгофа для контура 1-2-4-1:
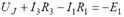
Откуда
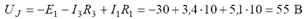
Тогда
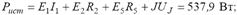
Задача 1.1.3 Методом контурных токов определить токи в ветвях схемы (рисунок 3), если Е1=50 В, J1=1 A, J2=2 A, R1=R2=R3=R4=10 Ом, R5=R6=5 Ом.
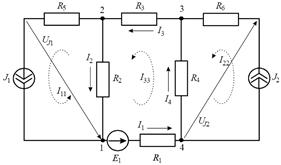
Рис. 3
Решение:
Данная электрическая цепь содержит две ветви с идеаль-ными источниками тока J1 и J2. Выбираем контуры таким образом, чтобы эти ветви являлись образующими, будем считать контурные токи равными токам источников тока: I11 = J1 и I22 = J2. Неизвестным является контурный ток I 33.
Запишем уравнение для третьего контура:
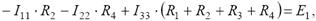
Так как величины токов I11 и I22 известны, то их произведения на взаимные сопротивления контуров можно перенести в правую часть уравнения. Тогда уравнение примет вид:
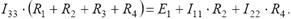
Выразим контурный ток I 33:
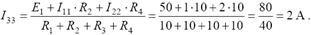
Методом наложения определим неизвестные токи в ветвях:
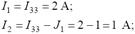
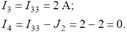
Напряжение на зажимах источников тока UJ1 и UJ2 определим из уравнений, записанных по второму закону Кирхгофа:
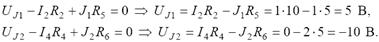
Определяем мощность источников энергии:
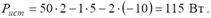
Мощность потребителей определим по формуле:
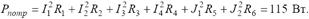
Задача 4. Методом контурных токов определить токи в ветвях схемы (рисунок 4), если Е1=10 В, Е2=30 В, J=2 A, R1=R2=R3=R4= R5=5 Ом.
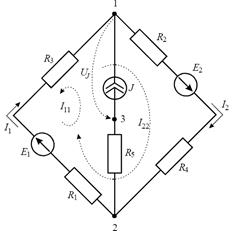
Рис. 4
Решение:
Выражаем контурный ток I22:
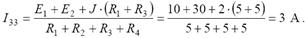
Определим величины токов в ветвях схемы.
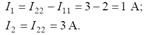
Уравнение мощности источников для данной схемы выглядит следующим образом:
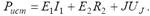
Для определения напряжения на зажимах источника тока запишем уравнение по второму закону Кирхгофа для контура 1-3-2-1:
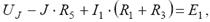
Откуда
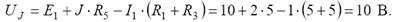
Подставим полученное значение напряжения в формулу и определим мощность источников:
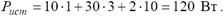
Определим мощность потребителей:
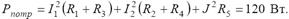
3.3. Задачи для самостоятельно решения
Задача 1. Электрическая цепь (рисунок 5) питается двумя источниками тока. Определить напряжение на каждом из источников, если их токи J1 = 20 мА, J2 = 10 мА, R1 = 2 кОм, R2 = 4 кОм, R3 = 6 кОм, R4 = 4 кОм
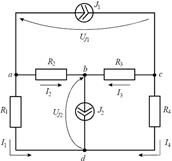
Рис. 5
Задача 2. Определить токи в ветвях схемы, рисунок 6, методом контурных токов, если известно: E1 = 120 B, E2 = 88 B, J = 10 А, R1 = 2 Ом, R2 = 8 Ом, R3 = R4 = 12 Ом, R5 = 4 Ом, R6 = 2 Ом.
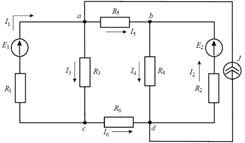
Рис. 6
Задача 3. Определить токи в ветвях электрической цепи, изображенной на рисунке 7, используя метод контурных токов. Параметры элементов цепи: E1 = 168 B, E2 = 210 B, R1 = R5 = 45 Ом, R2 = 30 Ом,
R3 = R4 = 30 Ом, R6 = 75 Ом, R7 = 27 Ом.
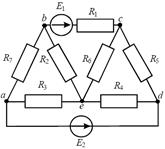
Рис. 7
Задача 1.2.4 Рассчитать электрическую цепь методом контурных токов (рисунок 8) при известных параметрах элементов: E = 50 B, J = 20 А, R1 = R2 = R3 = 8 Ом, R4 = 12 Ом.
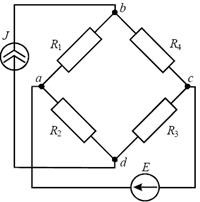
Рис. 8
Задача 1.2.5 Методом контурных токов определить токи в цепи (рисунок 9), если Е1 = Е2 = Е4 = 30 В, Е3 = 20 В, J1 = J4 = 1 A, J2 = 2 A, J3 = 3 A, R1 = R2 = R3 = R4 = R5 = 10 Ом.
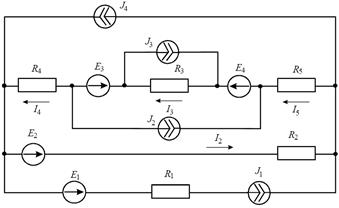
Рис. 9
3.3. Домашнее задание ( задачи для самостоятельного решения)
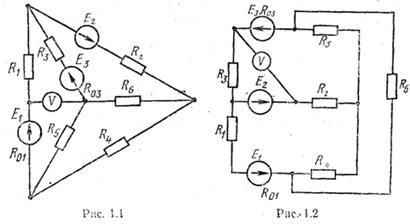
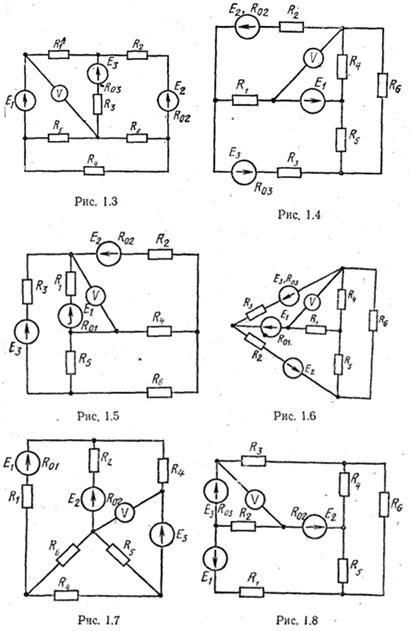
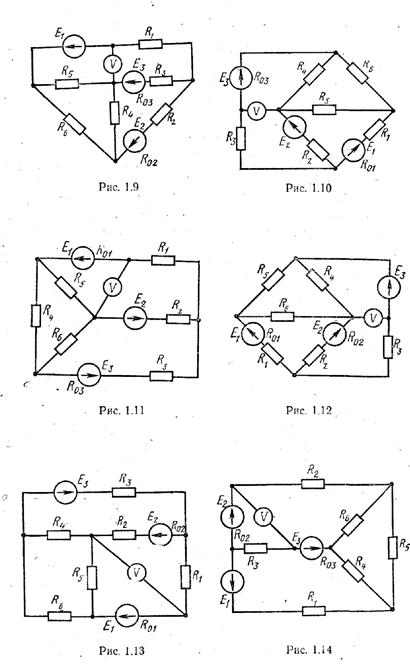
Для электрической цепи, схема которой изображена на рис. 1.1–1.32, по заданным в соответствии с вариантом задания в табл. 1 сопротивлениям и э. д. с. выполнить следующее:
1) составить систему уравнений, необходимых для опре-деления токов по первому и второму законам Кирхгофа;
2) найти все токи, пользуясь методом контурных токов;
3) определить показание вольтметра и составить баланс мощностей для заданной схемы;
Результаты выполнения домашнего задания оформить отчетом, защитить и сдать преподавателю, ведущему практические занятия.
Исходные данные к домашнему заданию
1. Схемы электрических цепей
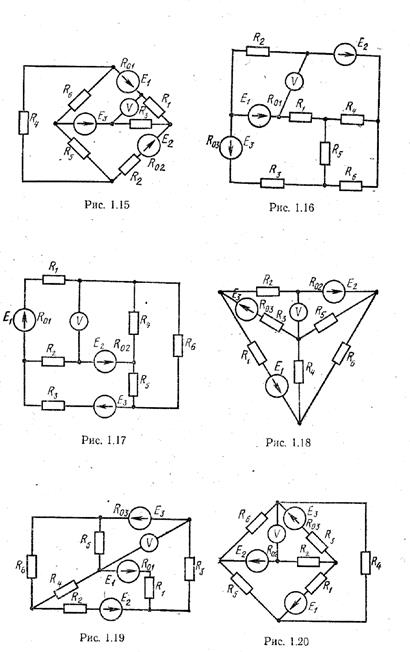
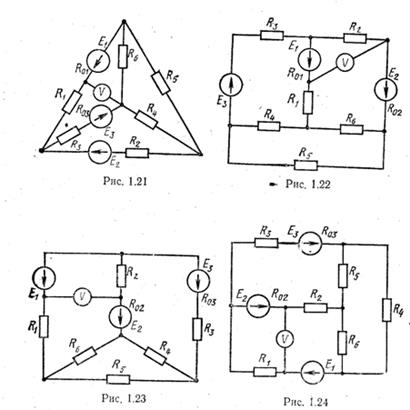
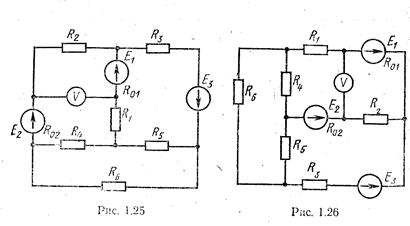
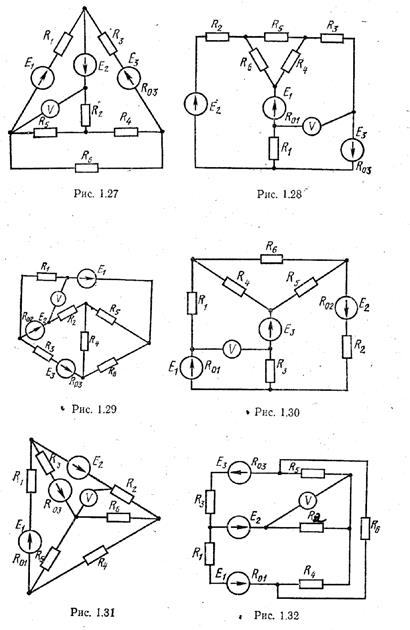
2. Параметры элементов электрических цепей
Таблица 1
Значения параметров элементов схем
| Номера | |||||||||||||
| Варианта | Рисунка | Е1, В | Е2, В | Е3, В | R01, Ом | R02, Ом | R03, Ом | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом |
| 1 | 1. 1 | 22 | 24 | 10 | 0,2 | - | 1,2 | 2,0 | 1,0 | 8,0 | 4,0 | 9,8 | 6,0 |
| 2 | 1. 2 | 55 | 18 | 4 | 0,8 | - | 0,8 | 8,0 | 4,0 | 3,0 | 2,0 | 4,0 | 4,0 |
| 3 | 1. 3 | 36 | 10 | 25 | - | 0,4 | 0,5 | 4,0 | 8,0 | 3,0 | 1,0 | 2,0 | 7,0 |
| 4 | 1. 4 | 16 | 5 | 32 | - | 0,6 | 0,8 | 9,0 | 3,0 | 2,0 | 4,0 | 1,0 | 5,0 |
| 5 | 1. 5 | 14 | 25 | 28 | 0,9 | 1,2 | - | 5,0 | 2,0 | 8,0 | 2,0 | 2,0 | 6,0 |
| 6 | 1. 6 | 20 | 22 | 9 | 0,1 | - | 1,1 | 1,0 | 2,0 | 6,0 | 3,0 | 8,0 | 4,0 |
| 7 | 1. 7 | 5 | 16 | 30 | 0,4 | - | 0,7 | 6,0 | 4,0 | 3,0 | 2,0 | 5,0 | 1,0 |
| 8 | 1. 8 | 10 | 6 | 24 | 0,8 | 0,3 | - | 3,5 | 5,0 | 6,0 | 6,0 | 3,0 | 3,0 |
| 9 | 1. 9 | 6 | 20 | 4 | - | 0,8 | 1,2 | 4,0 | 6,0 | 4,0 | 4,0 | 3,0 | 1,0 |
| 10 | 1. 10 | 21 | 4 | 10 | - | 0,2 | 0,6 | 5,0 | 7,0 | 2,0 | 8,0 | 1,0 | 2,0 |
| 11 | 1. 11 | 4 | 9 | 18 | 0,8 | - | 0,4 | 2,7 | 9,0 | 4,0 | 8,0 | 9,5 | 4,0 |
| 12 | 1. 12 | 4 | 24 | 6 | 0,9 | - | - | 9,0 | 8,0 | 1,0 | 6,0 | 9,7 | 5,0 |
| 13 | 1. 13 | 16 | 8 | 9 | 0,2 | 0,6 | - | 2,5 | 6,0 | 6,0 | 5,0 | 9,3 | 2,0 |
| 14 | 1. 14 | 48 | 12 | 6 | 0,8 | 1,4 | 1,2 | 4,2 | 4,0 | 2,0 | 9,5 | 6,0 | 8,0 |
| 15 | 1. 15 | 12 | 36 | 12 | - | 0,4 | - | 3,5 | 5,0 | 1,0 | 5,0 | 6,0 | 8,0 |
| 16 | 1. 16 | 12 | 6 | 40 | 1,2 | 0,6 | 0,4 | 2,0 | 3,0 | 8,0 | 5,0 | 7,0 | 6,0 |
| 17 | 1. 17 | 8 | 6 | 36 | 1,3 | - | 0,5 | 3,0 | 2,0 | 1,0 | 6,0 | 8,0 | 4,0 |
| 18 | 1. 18 | 72 | 12 | 4 | 0,7 | 1,5 | 0,8 | 6,0 | 1,0 | 9,0 | 4,0 | 9,0 | 2,0 |
| 19 | 1. 19 | 12 | 30 | 9 | - | 0,4 | 1,2 | 2,5 | 1,0 | 4,0 | 9,5 | 2,0 | 3,0 |
| 20 | 1. 20 | 9 | 6 | 27 | 0,5 | - | - | 3,5 | 2,0 | 3,0 | 3,0 | 1,0 | 3,0 |
| 21 | 1. 21 | 15 | 63 | 6 | - | 1,0 | 0,8 | 4,5 | 2,0 | 8,0 | 8,5 | 4,0 | 3,0 |
| 22 | 1. 22 | 54 | 27 | 3 | 1,0 | 0,9 | 1,2 | 5,0 | 3,0 | 1,0 | 2,0 | 9,5 | 2,0 |
| 23 | 1. 23 | 36 | 9 | 24 | 1,2 | 0,7 | - | 8,0 | 3,0 | 1,0 | 4,0 | 2,0 | 3,0 |
| 24 | 1. 24 | 3 | 66 | 9 | - | 0,4 | - | 3,0 | 4,0 | 2,0 | 1,0 | 5.0 | 4,0 |
| 25 | 1. 25 | 12 | 30 | 25 | - | 0,8 | 1,0 | 1,0 | 4,0 | 2,0 | 2,0 | 7.0 | 5.0 |
| 26 | 1. 26 | 30 | 16 | 10 | 1,0 | - | 0,8 | 1,0 | 5,0 | 1,0 | 1,0 | 6,0 | 5.0 |
| 27 | 1. 27 | 10 | 32 | 10 | 0,6 | - | 0,2 | 2,0 | 5.0 | 3,0 | 1,0 | 8,0 | 2,0 |
| 28 | 1. 28 | 5 | 10 | 36 | 0,6 | 0,4 | - | 1,5 | 6,0 | 1,0 | 7,0 | 1,0 | 2,0 |
| 29 | 1. 29 | 40 | 25 | 8 | 0,3 | 0,6 | 1,2 | 1,2 | 6,0 | 3,0 | 2,0 | 2,0 | 1,0 |
| 30 | 1. 30 | 8 | 40 | 10 | - | 1,2 | 0,8 | 3,0 | 3,0 | 2,0 | 4,0 | 3,0 | 6,0 |
| 31 | 1.31 | 22 | 24 | 10 | 0,8 | - | 0,5 | 5,0 | 3,0 | 3,0 | 3,0 | 4,0 | 4,0 |
| 32 | 1.32 | 55 | 18 | 4 | 0,2 | 0,3 | 0,8 | 2,0 | 1,0 | 8,0 | 4,0 | 3,0 | 7,0 |
Список использованных источников
1. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи: Учеб. для вузов /Л.А. Бессонов. – 10-е изд. – М.: Гардарики, 2000. – 638с.: ил.
2. Гольдин О.Е. и др. Программированное изучение теоретических основ электротехники: Учебное пособие. /О.Е.Гольдин, А.Е.Каплянский, Л.С.Полотовкский. – М: Высшая школа, 1978. –287с.: ил.
3. Сборник задач и упражнений по теоретическим основам электротехники: Учебное пособие для вузов. /Под ред. П.А. Ионкина. – М.: Энергоиздат, 1982. – 767с.: ил.
4. Сборник задач по теоретическим основам электротехники: Учебное пособие для вузов. /Под ред. Л.А. Бессонова. – 3-е изд., переработ. и доп. – М.: Высшая школа, 1980. – 472с.: ил
5. Сборник задач по теоретическим основам электротехники: Учеб. пособие для вузов /Под ред. Л.А. Бессонова. – 3-е изд., переработ. и доп. – М.: Высшая школа, 1988. – 543с.: ил.
6. Репьев Ю.Г., Семенко Л.П., Поддубный Г.В. Теоретические основы электротехники. Теория цепей. – Краснодар: Краснодарский политехнический институт, 1990. – 299с.
7. Огорелков, Б.И. Методические указания к РГЗ № 1 по ТОЗ. Анализ установившихся процессов в электрических цепях постоянного тока /А.Н.Ушаков, Н.Ю.Ушакова, Б.И.Огорелков.– Оренбург: ОрПтИ, 1987. –46с.
8. Методы расчета электрических цепей постоянного тока: Методические указания /Б.И.Огорелков, А.Н.Ушаков, Н.Ю.Ушакова. – Оренбург: ОрПтИ, 1990.-45с.
1. Григорьев С.И., Глебова Е.Г., Калашникова Л.А., Киселева Г.М. Методические указания к выполнению контрольного задания №1 «Рас-чет сложной линейной цепи постоянного тока» по курсу «Теоретические основы электротехники» для студентов заочной формы обучения элек-тротехнических специальностей.– Харьков: ХГПУ, 2000.
2. Глебова Е.Г., Кравченко Г.С. Методические указания к вы-полнению расчётно-графического задания №1 «Расчет сложной линей-ной цепи постоянного тока» по курсу «Теоретические основы электро-техники» для студентов электротехнических специальностей.– Харьков: ХПИ, 1982.
3. Бессонов Л.А. и др. Теоретические основы электротехники. Методические указания и контрольные задания для студентов заочников электротехнических специальностей вузов.– М.: Высш. шк., 1987.
4. Самсонов В.П. Теорія електромагнітних кіл. Ч.1. «Аналіз електричних кіл постійного та змінного струму».– К., 1994.
5. Боев В.М., Казаковцева Л.В., Самсонов В.П. «Методические указания по выполнению расчетно-графического задания по теме «Расчет линейных электрических цепей постоянного и гармонического тока» - Харьков: НТУ «ХПИ», 2003.
6. Фаронов В.В. «Турбо Паскаль 7.0». Начальный курс: Учебное пособие.– М., 2000.
7. Шебес М.Р. Теория линейных электрических цепей в упражнениях и заданиях.– М. Высш. шк., 1973.








