2. Динамика поступательного движения точки и твердого тела

Дата: 2025-05-01; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

d p = ån

Второй закон Ньютона классической механики: dt i=1

Если не известен точный закон, по которому изменяется полная сила

F (t) = å F (t),

i=1 i

действующая на тело, то можно использовать понятие средней

силы

за какой-то промежуток времени

Dt = t

1 от момента

1 до 2 :

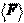
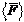
= 1 t2 F (t)dt.

Dt t1

Тогда уравнение второго закона Ньютона можно записать в виде

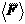Dp = Dt,

где Dp = p2

- p - изменение импульса за тот же промежуток времени.

Сила, действующая на материальную точку, движущуюся по кривой, может быть разложена на две составляющие – тангенциальную и нормальную.

Ft = m at

= m dV t ,

dt

F = ma

2

m n,

Нормальная, или центростремительная сила R

·

Сила трения скольжения

тр = -mN ,

· Сила упругости

упр

= -kDl = -k(x - x ),

F = G 1 2 12 ,

G = 6,67 ×10-11 Н × м

· Сила гравитационного взаимодействия

гравитационная постоянная

r 2 r

где

кг 2 -

· Закон сохранения импульса: «Полный импульс замкнутой системы есть

n

величина постоянная»

p = å mV

= const .

· Применение закона сохранения импульса к соударению двух тел:

mV + m V = mU + m U ,

1 1 2 2 1 1 2 2

· При неупругом ударе, когда тела движутся вместе после соударения, их общая скорость U становится равной

U = mV + m V

+

m .

3. Динамика вращательного движения твердого тела

Момент силы относительно неподвижной точки:

M = [r ´ F ],

· Момент силы F относительно оси вращения M = F^l ,

Основной закон динамики вращательного движения твердого тела относитель-

но неподвижной оси

d (Jw) ,

M

dt

· Теорема Штейнера:

J = J0 + m a2 ,

4. Законы сохранения импульса и механической энергии

· Закон сохранения импульса замкнутой системы

N

i=1 , или

N

i=1 ,

· Работа, совершаемая постоянной силой DA = F ×Dr = FDr cosa

· Работа, совершаемая переменной силой

A = ò F × cosa × dS

S

· Средняя мощность за интервал времени Dt

N = DA = F V

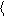
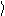
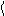Dt

cosa .

· Мгновенная мощность

N = dA = FV cosa

dt

mV 2

T

. Кинетическая энергия тела,

движущегося поступательно 2 .

Потенциальная энергия тела, поднятого на высоту h /

U = mgh.

kDl 2

U =

2 ,

Потенциальная энергия упругодеформированного тела

· Применение законов сохранения энергии и импульса к столкновению абсо- лютно упругих тел: при центральном ударе скорости тел после соударения рав- ны

U = 2m V + (m - m )V U = 2mV + (m - m )V

2 2 1 2 1 1 1 2 1 2

1 m + m , 1 m + m ,

Кинетическая энергия тела, вращающегося относительно неподвижной оси,

Jw 2

T =

2 .

Jw 2 + mV 2

Кинетическая энергия тела, катящегося по плоскости,

2 2 _.

5. Закон сохранения момента импульса

· Момент импульса материальной точки с импульсом p относительно

начала координат

L = [r ´ p],

Момент импульса (момент количества движения) твердого тела относительно оси вращения:

L = å mVr = J w ,

Закон сохранения момента импульса (момента количества движения):

N

L = const,

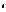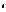å J w = const

i=1 .

· Закон сохранения момента импульса для тела, вращающегося на оси, мо- мент инерции которого меняется:

J w = J w

1 1 2 2 ,

6. Внутренняя энергия и теплоемкость газов

Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева)

m

pV = M RT,

Закон Бойля-Мариотта: pV=const при T=const, m=const.

V = T

1 1

Закон Гей-Люссака: V=V₀(1+at ) или V2 2 при р=const, m= const.

p = T

1 1

Закон Шарля: р=р₀(1+at) или 2 T при V=const, m=const,

æ n m ö

Закон Дальтона для давления смеси идеальных газов:

pV = çåi ÷RT

è i=1 M i ø

Основное уравнение молекулярно-кинетической теории идеальных газов

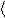
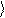p = 1 nm V 2

p=nkT.

3 0 кв ,

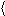
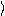Средняя кинетическая энергия молекулы (с учетом поступательного и враща-

тельного движения)

e = 1 kT, 2

Средняя кинетическая энергия поступательного движения молекулы ⁽ i по с т = 3)

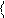
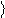
e = 3 kT

2 .

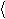
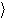e = i в р kT

Средняя кинетическая энергия вращательного движения молекулы

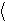
Средняя кинетическая энергия колебательного движения молекулы e

2 ,

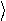= kT .

Внутренняя энергия идеального газа:

U = V

i RT =

2

m i RT M 2 .

7. Первое и второе начала термодинамики. Энтропия. Циклы

Первое начало термодинамики: Q=DU+A,

DU = i m RDT

Изменение внутренней энергии идеального газа

2 M .

Молярные и удельные теплоемкости газа при постоянном объеме и постоян- ном давлении:

C = i R c

= i R C

= i + 2 R

c = i + 2 R

V 2 ,

V , уд

2 m ; P 2

P , уд

2 m .

Уравнение Майера:

= C + R

Работа, совершаемая газом при изменении его объема: dA=pdV.

m

Работа газа при изобарном процессе: A=p(V₂-V₁) или A= M R(T₂-T₁).

m

При изотермическом процессе: A= M RT

V

ln 2

1

m

или A= M RT

p

ln 2

1 .

Уравнение Пуассона для адиабатного процесса:

g g-1

g 1-g

i + 2

pV =const, TV

= const, T p

= const, C V = 2

Работа в случае адиабатического процесса:

m RT m é

æ V ög -1 ù

p V é

æ V ög -1 ù

A = g 1

ê1- ç 1 ÷

ú = 1 1 ê1- ç 1 ÷ ú

A= M С_V(T₂-T₁) или,

-1 M

èV2 ø úû

g -1 êë

èV2 ø

úû ,

h = A = Q - Q

Термический КПД теплового двигателя 1 ,

h = T - T

Q Q

h = Q - Q

1 2

КПД цикла Карно 1

1 2

или 1 ,

Изменение энтропии при равновесном переходе системы из состояния 1 в со-

DS = S

- S = 2 dQ

стояние 2:

1®2

2 1 ò

1 T

8. Явление переноса

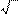
Среднее число соударений, испытываемых одной молекулой газа в единицу

времени ^{z =}

2pd 2 n V ,

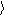l = 1

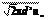Средняя длина свободного пробега молекул газа