Тематический план по семестрам
Первый курс
1. Физические основы классической механики
1.1. Элементы кинематики материальной точки. Перемещение и путь. Скорость и ускорение. Тангенциальное и нормальное ускоре- ния.
1.2. Движение материальной точки по окружности. Связь меж- ду линейными и угловыми характеристиками движения.
1.3. Динамика материальной точки и поступательного движе- ния абсолютно твердого тела. Законы Ньютона и инерциальные си- стемы отсчета. Закон сохранения импульса. Уравнение движения тела переменной массы.
1.4. Преобразования Галилея. Механический принцип относи- тельности. Границы применимости классической механики.
1.5. Виды сил в механике. Поле как форма материи, осуществ- ляющая силовое взаимодействие между частицами вещества. Закон всемирного тяготения. Потенциал гравитационного поля. Сила тяже- сти и вес тела.
1.6. Работа силы. Консервативные поля, силы, системы. Мощ- ность. Механическая энергия. Потенциальная энергия. Кинетическая энергия. Энергия упруго деформированного тела. Закон сохранения энергии в механике. Удар абсолютно упругих и неупругих тел.
1.7. Динамика вращения. Момент силы. Момент инерции тела. Момент импульса тела. Основной закон динамики вращательного движения твердого тела. Закон сохранения момента импульса. Кине- тическая энергия вращающегося тела.
Примеры решения задач
Пример 1. Тело вращается вокруг неподвижной оси по закону
j=А+Вt+Сt2, где А = 10рад, В = 20рад/с, С = -2рад/с2. Найти полное ускорение точки, находящейся на расстоянии r = 0,1м от оси враще- ния, для момента времени t = 4с.
Дано:
j = А+Вt+Сt2
А=10 рад В=20 рад/с r = 0,1 м С=-2рад/с2 t=4 с

 а - ?
а - ?
| Решение: аt аn а Рисунок 1 полное ускорение a точки, движущейся по кри- вой линии, может быть найдено как геометриче- ская сумма тангенциального ускорения аn, направленного к центру кривизны |




 траектории (см. рисунок 1). a = at + an , т.к. at ^ an ,
траектории (см. рисунок 1). a = at + an , т.к. at ^ an ,
 то а = (a t2 +an 2 ). Тангенциальное и нормальное ускорения то- чек вращающегося тела выражаются формулами:
то а = (a t2 +an 2 ). Тангенциальное и нормальное ускорения то- чек вращающегося тела выражаются формулами:
ar=er; аn = w2r ,
где w - угловая скорость тела; e - его угловое ускорение.
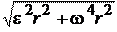
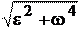 Тогда а = = r
Тогда а = = r
Угловую скорость найдем, взяв первую производную от угла поворота по времени:
w = ¶j/¶t = B + 2Ct
В момент времени t = 4с угловая скорость
w= [20+2(-2)4] рад/с = 4 рад/с.
Угловое ускорение найдем, взяв первую производную от угло- вой скорости по времени:
e = ¶w/¶t = 2С = -4рад/ с2.
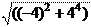 Угловое ускорение не зависит от времени, т.е. постоянно. Под- ставляя найденные значения и исходные данные, получим:
Угловое ускорение не зависит от времени, т.е. постоянно. Под- ставляя найденные значения и исходные данные, получим:
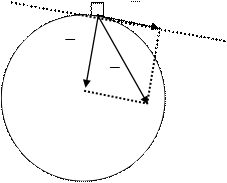 а = 0,1·
а = 0,1·
= 1.65м/с2.
Ответ: а = 1.65м/с2.
Пример 2. Два автомобиля выходят из одного пункта в одном направлении. Первый выходит на 20 с позже второго. Оба движутся с ускорением 0,4 м/с2. Через сколько времени, считая от начала движе- ния первого автомобиля, расстояние между ними станет 240м?
Дано: Решение.
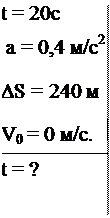 Запишем уравнения движения двух автомобилей:
Запишем уравнения движения двух автомобилей:
S1 =
at 2
 2
2
; S2 =
a(t + t ) 2

|
2 ;
DS = S2 - S1 =
a(t + t ) 2

|
2
at 2
 - 2 ;
- 2 ;
at 2 + 2att + at 2 - at 2
DS = 1 1 ,
2
откуда находим время.


 t = 2DS - at1 = DS - t 1 ;
t = 2DS - at1 = DS - t 1 ;
2at1 at1 2
240
 t = 0,4 × 20
t = 0,4 × 20
- 20 = 20(c). Проверка размерности:
 2
2
[t]
éм × с2 ù
 = ê м × с ú = с.
= ê м × с ú = с.
ë û
Пример 3. Тело брошено под углом 600 к горизонту со скоро- стью V0 = 20 м/с. Под каким углом к горизонту движется тело через 1,5 с после начала движения?
Дано: Решение
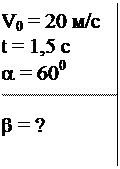 | |||
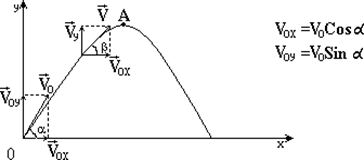 | |||
В верхней точке А траектории скорость, относительно оси у, равна 0 (Vy = V0- gt1 = 0), определим время подъёма до верхней точки траектории.
 t = V0y
t = V0y
= V0Sina ; t = 20 3 = 1,7c.

 1 g g 2 × 10
1 g g 2 × 10
Следовательно, тело через 1,5 с находится на подъёме.
V = V0x + Vy ;
 tgb =
tgb =
Vy V0x
= V0Sina - gt ; tgb =
 V0 Cosa
V0 Cosa
20 3 - 10 × 1,5
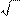
 2
2
 20 × 1
20 × 1
2
= 0,2; b @ 140.
Пример 4. Шарик, массой m, подвешенный на нити, отвели в сторону до уровня точки подвеса и отпустили. Найти натяжение нити в момент, когда она составит угол a с вертикалью.
 Дано:
Дано:
m
a
N = ?
Решение
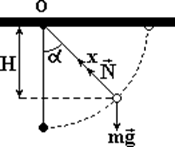
|
Выберем ориентацию оси координат Ох вдоль нити. По второму
закону Ньютона:
ma = N +
→
mg,
для оси Ох, max = N - mg×Cosa,
отсюда, учитывая, что ах - центростремительное ускорение, и то, что движение шарика происходит по окружности радиусом R, полу- чим:
|
2
 N = + mg ×Cosa, R
N = + mg ×Cosa, R
где V - скорость его движения в рассматриваемой точке.
Найдём скорость из закона сохранения энергии:
mg H = mV2
 |
.
2
Из рисунка видно: H = R× Cosa. Учитывая всё, можно записать

|
mgR× Cosa = mV2
2
откуда
 V = 2g× R × Cosa; тогда
V = 2g× R × Cosa; тогда
 N = m× 2gR × Cosa + mg × Cosa = 3mg × Cosa.
N = m× 2gR × Cosa + mg × Cosa = 3mg × Cosa.
R
Второй курс
2. Основы молекулярной физики и термодинамики
3.1. Статистический и термодинамический методы исследова- ния. Идеальный газ как молекулярно-кинетическая модель реальных газов. Изопроцессы. Закон Дальтона. Уравнение состояния идеально- го газа.
3.2. Основное уравнение молекулярно-кинетической теории га- зов. Средняя кинетическая энергия поступательного движения моле- кулы. Число степеней свободы. Внутренняя энергия идеального газа .
3.3. Распределение молекул газа по скоростям (распределение Максвелла). Идеальный газ в поле тяжести. Распределение Больцма- на.
3.4. Средняя длина свободного пробега молекулы. Явления пе- реноса (диффузия, вязкость и теплопроводность).
3.5. Первое начало термодинамики. Работа при расширении га- за. Применение первого начала термодинамики к изопроцессам и адиабатному процессу идеального газа. Зависимость теплоемкости идеального газа от вида процесса.
3.6. Круговые процессы (циклы). К.п.д. цикла. Второе начало термодинамики. Цикл Карно. К.п.д. цикла Карно. Схема работы теп- ловой и холодильной машин. Энтропия. Необратимые процессы.
3.7. Реальные газы. Эффективный диаметр молекулы. Уравне- ние Ван-дер-Ваальса. Изотермы реальных газов. Фазовая диаграмма.
Примеры решения задач
1. Молекулярно-кинетическая теория идеальных газов
Пример 2. Определить, сколько киломолей и молекул водорода со- держится в объеме 50 м3 под давлением 767 мм рт. ст. при температуре 18°С. Какова плотность и удельный объем газа?
| Дано: V = 50 м3 Ρ = 767 мм. рт. ст. @ 767·133 Па Т = 291 К | Решение: На основании уравнения Менделее- ва – Клайперона: pV = nRT устанавливаем |
| М = 2 кг/моль | число киломолей ν, содержащихся в |
| ν – ? | заданном объеме V. Зная р - давле- |
| N – ? | ние, V – объем, Т – температуру га- |
| ρ – ? | за, R – молярную газовую постоян- |
| d – ? | ную |
можно определить ν:
 n = pV ;
n = pV ;
RT
n = 767 ×133 × 50
 8,31×103 × 291
8,31×103 × 291
= 2,11 (кмоль)
Число молекул N, содержащихся в данном объеме, находим, используя число Авогадро NА (которое определяет какое количество молекул содержится в одном киломоле). Общее количество молекул, находящихся в массе m данного газа, может быть установлено, так как известно число молей ν.
N = nNA .
Подставляя в формулу число киломолей, устанавливаем число
молекул, содержащихся в объеме V:
N = 2,11× 6,02 ×1026
= 12,7 ×1026.
Плотность газа ρ = m/V определяем из уравнения Менделеева - Клайперона:
 pV = m
pV = m
M
RT ;
 r = pM .
r = pM .
RT
Подставляя числовые значения в единицах СИ в формулу, опре-
делим плотность газа:
 r = 767 ×1,33 ×102 × 2 =
r = 767 ×1,33 ×102 × 2 =
8,31×103 × 291
8,44
×10-2
(кг/м
3).
Удельный объем газа d определяем из уравнения Менделеева - Клайперона:
 d = V =
d = V =
m
RT ;
 pM
pM
Ответ: 11,9 м3/кг.
8,31×103 × 291
 d = 767 ×133 × 2
d = 767 ×133 × 2
» 11,9
|
 (м3/кг).
(м3/кг).
Пример 3.. В сосуде объемом 2 м3 находится смесь 4 кг гелия и 2 кг водорода при температуре 27°С. Определить давление и мо- лярную массу смеси газов.
Дано:
V = 2 м3
m1= 4 кг
М1= 4·10-3 кг/кмоль
Решение:
 Воспользуемся уравнением Менделе- ева - Клайперона, применив его к ге- лию и водороду:
Воспользуемся уравнением Менделе- ева - Клайперона, применив его к ге- лию и водороду:
m2= 2 кг
М2= 2·10-3
кг/кмоль
p1V
= m1 RT
 M
M
(1)
Т1= 300 К
р - ?
М - ?
p2V
1
 = m2 RT M 2
= m2 RT M 2
(2)
где р1 – парциальное давление гелия;
m1 – масса гелия;
М1 – его молярная масса; V – объем сосуда; Т – температура газа; R = 8,31 Дж/(моль·К) –молярная газовая постоянная; р2 – парциальное давление водорода; m2 – масса водорода; М2 – его молярная масса.
По закону Дальтона:
p = p1 + p2
(3)
Из уравнений (1) и (2) выразим р1 и р2 и подставим в уравнение
 (3):
(3):

 m1RT
m1RT
m2 RT
æ m1
m2 ö RT
 |  |
p =
M1V
+
M 2V
= ç
è M1
+ ÷
M 2 ø V
(4)
С другой стороны, уравнение Менделеева - Клайперона для сме-
си газов имеет вид:
pV = æ m1 + m2 öRT

(5)
|
ç ÷
è ø
Сравнивая (4) и (5) найдем молярную массу смеси газов по фор- муле:
 М = m1 + m2
М = m1 + m2
= m1 + m2 , (6)


 m1 + m2 M1 M 2
m1 + m2 M1 M 2
n1 + n2
где ν1 и ν2 – число молей гелия и водорода соответственно.
|
|
p = æ 4 + 2 ö × 8,31× 300 » 2,5 ×106 (Па).
 |  |  |
ç 4 ×10-3 2 ×10-3 ÷ 2
M = 4
4 + 2
|


 + 2
+ 2
= 3 ×10-3
(кг/моль).
4 ×10-3
Ответ: 3·10-3 кг/моль.

2 ×10-3
2. Основы термодинамики
Пример 4. Чему равны средние кинетические энергии поступатель- ного и вращательного движения молекул, содержащихся в 2 кг водорода при температуре 400 К.
| Дано: т = 2 кг Т = 400 К М = 2·10 –3 кг/моль | Решение: Считаем водород идеальным газом. Молекула водорода – двухатомная. Связь между атомами считаем жест- кой, тогда |
| <Eпост> - ? <Eвр> - ? |
число степеней свободы молекулы водорода равно 5. В среднем на
одну степень свободы приходится энергия: < E i
>= kT .
 2
2
Поступатель-
ному движению приписывается три (i = 3), а вращательному две
(i= 2) степени свободы. Тогда энергия одной молекулы:
< Eпост
>= 3 kT , 2
< Eвр
>= 2 kT .
 2
2
 Число молекул, содержащихся в массе газа m:
Число молекул, содержащихся в массе газа m:
N = nNA
= m N M
A, где ν – число молей, NA – число Авогадро. Тогда
 средняя кинетическая энергия поступательного движения молекул
средняя кинетическая энергия поступательного движения молекул
водорода будет:
< E >= m N

3 kT = 3

m RT
, (1)
пост

M A 2 2 M
где R = kNA – молярная газовая постоянная.
Средняя кинетическая энергия вращательного движения моле-
кул водорода:
< Eвр >= M
RT . (2)

|
Подставляя числовые значения и формулы (1) и (2), имеем:
< Eпост
>= 3 × 2 × 8,31× 400 = 49,86 ×105 (Дж) = 4986(кДж);
 2 × 2 ×10-3
2 × 2 ×10-3
< Евр
>= 2 × 8,31× 400 = 33,24 ×105 (Дж) = 3324(кДж)
 2 ×10-3
2 ×10-3
Ответ: 4986 кДж, 3324 кДж.
Пример 5. Определить скорость вылета поршня массой 4 кг из ци- линдра при адиабатном расширении кислорода в 40 раз, ес- ли начальное давление воздуха 107 Па, а объем 0,3 л.
| Дано: Т = 4 кг V2/V1 = 40 p1 = 10 7Па V1 = 0,3 л = 3·10-4 м3 | Решение: Работа А, совершаемая адиабатически рас- ширяющимся воздухом, в данном случае идет на увеличение кинетической энергии поршня, т. е |
| υ - ? |
|
2
 A = ,
A = ,
2
где т и υ – масса и скорость поршня.
Для подсчета работы адиабатически расширяющегося газа вос-
p V é
æ V ög-1 ù
пользуемся формулой:
A = 1 1 ê1 - ç 1 ÷
ú , где γ – отношение теп-
g -1 êë
èV2 ø úû
|
лоемкостей газа при постоянном давлении и постоянном объеме (для кислорода γ =1,4).
107 × 0,3 ×10-3
 A =
A =
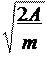
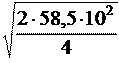 0,4
0,4
(1 - 0,22) = 5,85 ×103
(Па).
Так как
2
 A = , то 2
A = , то 2
υ =
Ответ: 54 м/с.
, υ =
» 54(м/с).
Лабораторные работы (Приложение)
1. Исследование законов свободного падения тел.
2. «Проверка законов динамики и закона сохранения механической энергии методом Максвелла»
3. Измерение отношения теплоемкости воздуха при постоянном давлении к его теплоемкости при постоянном объеме.








