390 раз больше радиуса Rл Луны и вес тела на Луне в 6 раз меньше веса тела на Земле.

Дата: 2025-05-01; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

8. Шарик массой т=60 г колеблется с периодом Т=2 с. В начальный момент времени смещение шарика x₀=4,0 см и он обла- дает энергией Е=0,02Дж. Записать уравнение простого гармониче- ского колебания шарика и закон изменения возвращающей силы с течением времени.

Вариант 1

1. Тело брошено вертикально вверх с начальной скоростью u₀ = 4

м/с. Когда оно достигло верхней точки полета из того же начально-

го пункта, с той же начальной скоростью u₀ вертикально вверх бро-

шено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивление воздуха не учитывать.

2. При горизонтальном полете со скоростью u = 250 м/с снаряд

массой m=8кг разорвался на две части. Большая часть массой m₁ = 6

кг получила скорость u₁ = 400 м/с в направлении полета снаряда.

Определить модуль и направление скорости ряда.

u₂ меньшей части сна-

3. В деревянный шар массой m₁ = 8 кг, подвешенный на нити

длиной l =1,8 м, попадает горизонтально летящая пуля массой m₂ = 4 г. С какой скоростью летела пуля, если нить с шаром и за- стрявшей в нем пулей отклонилась от вертикали на угол a =3°? Раз- мером шара пренебречь. Удар пули считать прямым, центральным.

4. Определить работу растяжения двух соединенных последова- тельно пружин жесткостями k 1 = 400 Н/м и k 2 = 250 Н/м, если пер-

вая пружина при этом растянулась на х₁ = 2 см.

5. Шарик массой т = 60 г, привязанный к концу нити длиной

l1 =1,2 м, вращается с частотой n = 2c , опираясь на горизонтальную

-1

плоскость. Нить укорачивается, приближая шарик к оси до рас- стояния l₂=0,6 м. С какой частотой п₂ будет при этом вращаться шарик? Какую работу А совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.

6.

На скамье Жуковского сидит человек и держит на вытянутых руках гири массой т = 5 кг каждая. Расстояние от каждой гири до оси скамьи l=70см. Скамья вращается с частотой п = 1с -1 . Как из- менится частота вращения скамьи и какую работу А произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до l = 20 см? Момент инерции человека и ска- мьи (вместе) относительно оси J=2,5 кг∙м².

7. Определить напряженность G гравитационного поля на высоте h=1000 км над поверхностью Земли. Считать известными ускоре- ние g свободного падения у поверхности Земли и ее радиус R.

8. На стержне длиной l=30 см укреплены два одинаковых грузи- ка: один - в середине стержня, другой - на одном из его концов. Стержень с грузами колеблется около горизонтальной оси, прохо- дящей через свободный конец стержня. Определить приведенную длину L и период Т простых гармонических колебаний данного фи- зического маятника. Массой стержня пренебречь.

Вариант 2

1. Материальная точка движется прямолинейно с ускорением a =5м/с². Определить, на сколько путь, пройденный точкой в п-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять u₀ = 0.

2. С тележки, свободно движущейся по горизонтальному пути со

скоростью u₁ =3 м/с, в сторону, противоположную движению те-

лежки, прыгает человек, после чего скорость тележки изменилась и

стала равной u₁ =4 м/с. Определить горизонтальную составляющую

скорости

u2 x

человека при прыжке относительно тележки. Масса те-

лежки

m₁ = 210 кг, масса человека

m₂ =70 кг.

3. По небольшому куску мягкого железа, лежащему на наковальне

массой

m₁ =300 кг, ударяет молот массой

m₂ = 8 кг. Определить КПД

h удара, если удар неупругий. Полезной считать энергию, затра- ченную на деформацию куска железа.

4. Из шахты глубиной Н = 600 м поднимают клеть массой т1 = 3,0 т на канате, каждый метр которого имеет массу т =1,5 кг. Ка- кая работа А совершается при поднятии клети на поверхность Земли? Каков коэффициент полезного действия h подъемного устройства?

5. По касательной к шкиву маховика в виде диска диаметром D= 75 см и массой т = 40 кг приложена сила F= 1 кН. Определить угловое ускорение e и частоту вращения п маховика через время t= 10 с после начала действия силы, если радиус r шкива равен 12 см. Силой трения пренебречь.

6. На скамье Жуковского стоит человек и держит руках стержень вертикально по оси скамьи. Скамья с человеком вращается с угло-

вой скоростью

w₁ = 4 рад/с. С какой угловой скоростью w₂

будет

вращаться скамья с человеком, если повернуть стержень так, что- бы он занял горизонтальное положение? Суммарный момент инер- ции человека и скамьи J=5 кг×м². Длина стержня l=1,8 м, масса m=6 кг. Считать, что центр масс стержня с человеком находится на оси платформы.

7. Какая работа А будет совершена силами гравитационного поля при падении на Землю тела массой т = 2 кг: 1) с высоты Н = 1000 км; 2) из бесконечности?

8. Точка участвует одновременно в двух взаимно перпендику-

лярных колебаниях, уравнения которых х=A1 sinw₁ t и y=A 2 cosw₂ t , где

A1 =8 см, A₂=4 см, w 1=w 2=2 с -1 . Написать уравнение траектории и построить ее. Показать направление движения точки.

Вариант 3

1. Две автомашины движутся по дорогам, угол между которыми

a = 60°. скорость автомашин u₁ = 54 км/ч и u 2=72км/ч. С какой

скоростью u удаляются машины одна от другой?

2. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом a = 30°

к линии горизонта. Определить скорость u₂ отката платформы, если

снаряд вылетает со скоростью u₁ =480 м/с. Масса платформы с

орудием и снарядами

m₂ =18т, масса снаряда

m₁ =60 кг.

3. Шар массой

m₁ = 1 кг движется со скоростью

u₁ = 4 м/с и стал-

кивается с шаром массой m₂ = 2 кг, движущимся навстречу ему со

скоростью

u₂ = 3 м/с. Каковы скорости u1

и u 2 шаров после удара?

Удар считать абсолютно упругим, прямым, центральным.

4. Пружина жесткостью k= 500 Н/м сжата силой F= 100 Н. Определить работу А внешней силы, дополнительно сжимающей

пружину еще на Dх = 2см.

5. На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой т=2 кг. Определить момент инер- ции J маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t= 3 с приобрел угловую скорость w = 9 рад/с.

6. Платформа в виде диска диаметром D= 3 м и массой m₁ =180

кг может вращаться вокруг вертикальной оси. С какой угловой

скоростью w₁ будет вращаться эта платформа, если по ее краю пой-

дет человек массой m₂=70 кг со скоростью u = 1,8 м/с относительно платформы?

7. Из бесконечности на поверхность Земли падает метеорит мас- сой т=30кг. Определить работу А, которая при этом будет совер- шена силами гравитационного поля Земли. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.

8.

Точка совершает простые гармонические колебания, уравнение которых х=A sinw t , где A=5 см, w =2с -1 . В момент времени, когда точка обладала потенциальной энергией П=0,1мДж, на нее дей- ствовала возвращающая сила F=5 мН. Найти этот момент времени t.

Вариант 4

1. Материальная точка движется прямолинейно с начальной ско- ростью u 0=10м/с и постоянным ускорением а = -5 м/с². Опреде-

лить, во сколько раз путь Ds , пройденный материальной точкой,

будет превышать модуль её перемещения начала отсчёта времени.

Dr спустя t=4 с после

2. Человек массой

m₁ =70 кг, бегущий со скоростью

u₁ =9 км/ч, дого-

няет тележку массой

m₂ =190кг, движущуюся со скоростью

u₂ =3,6

км/ч, и вскакивает на нее. С какой скоростью станет двигаться те- лежка с человеком? С какой скоростью будет двигаться тележка с че- ловеком, если человек до прыжка бежал навстречу тележке?

3. Шар массой

m₁ = 3 кг движется со скоростью

u₁ = 2 м/с и стал-

кивается с покоящимся шаром массой т₂ = 5 кг. Какая работа бу- дет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.

4. Две пружины жесткостью k1 = 0,5 кН/м и k 2 =1кН/м скреплены параллельно. Определить потенциальную энергию данной систе-

мы при абсолютной деформации Dх = 4 см.

5. Нить с привязанными к ее концам грузами массами m₁ = 50 г и

m₂ = 60 г перекинута через блок диаметром D= 4 см. Определить момент инерции J блока, если под действием силы тяжести грузов он получил угловое ускорение e = 1,5 рад/с². Трением и проскаль- зыванием нити по блоку пренебречь.

6. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол j повернется платформа, если человек пойдет вдоль края платформы и, обойдя ее, вернется в исходную (на платформе) точ- ку? Масса платформы т 1 = 280 кг, масса человека m₂ = 80 кг.

7. С поверхности Земли вертикально вверх пущена ракета со ско- ростью u =5км/с. На какую высоту она поднимется?

8. Определить частоту v простых гармонических колебаний диска радиусом R=20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.

Вариант 5

1. Велосипедист ехал из одного пункта в другой. Первую треть пути

он проехал со скоростью u₁ =18 км/ч. Далее половину оставшегося

времени он ехал со скоростью u₂ =22 км/ч, после чего до конечного

пункта он шел пешком со скоростью нюю скорость u велосипедиста.

u₃ = 5 км/ч. Определить сред-

2. Конькобежец, стоя на коньках на льду, бросает камень массой

m₁ = 2,5 кг под углом a = 30° к горизонту со скоростью u = 10 м/с.

Какова будет начальная скорость u₀ движения конькобежца, если

масса его m₂ = 60 кг? Перемещением конькобежца во время броска

пренебречь.

3. Определить КПД h неупругого удара бойка массой m₁ = 0,5 т,

падающего на сваю массой m₂ = 120 кг. Полезной считать энергию,

затраченную на вбивание сваи.

4. Какую нужно совершить работу А, чтобы пружину жестко- стью k=800Н/м, сжатую на х = 6 см, дополнительно сжать на D х = 8 см?

5. Стержень вращается вокруг оси, проходящей через его середину, согласно уравнению j = Аt+Вt³, где А=2 рад/с, В=0,2 рад/с³. Опре- делить вращающий момент М, действующий на стержень через время t=2 с после начала вращения, если момент инерции стержня J= 0,048 кг∙м 2 .

6. На скамье Жуковского стоит человек и держит в руке за ось велосипедное колесо, вращающееся вокруг своей оси с угловой

скоростью w₁ =25 рад/с. Ось колеса расположена вертикально и сов-

падает с осью скамьи Жуковского. С какой скоростью w 2 станет вра- щаться скамья, если повернуть колесо вокруг горизонтальной оси на угол a =90°? Момент инерции человека и скамьи J равен 2,5 кг∙м², момент инерции колеса J₀ = 0,5 кг∙м².

7. По круговой орбите вокруг Земли обращается спутник с перио- дом T=90мин. Определить высоту спутника. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.

8. Определить период Т простых гармонических колебаний диска радиусом R = 40 см около горизонтальной оси, проходящей через образующую диска.

Вариант 6

1. Тело брошено под углом a =30° к горизонту со скоростью u₀ =

30 м/с. Каковы будут нормальное а_п и тангенциальное аt

тела через время t=1с после начала движения?

ускорения

2. На полу стоит тележка в виде длинной доски, снабженной лег-

кими колесами. На одном конце доски стоит человек. Масса его m₁ =

60 кг, масса доски m₂ = 20 кг. С какой скоростью (относительно пола)

будет двигаться тележка, если человек пойдет вдоль нее со скоро- стью (относительно доски) u =1м/с? Массой колес и трением прене- бречь.

3. Шар массой

m₁ = 4 кг движется со скоростью

u₁ = 5 м/с и стал-

кивается с шаром массой m₂ = 6 кг, который движется ему навстре-

чу со скоростью

u₂ =2м/с. Определить скорости u1

и u2

шаров после

удара. Удар считать абсолютно упругим, прямым, центральным.

4. Если на верхний конец вертикально расположенной спираль-

ной пружины положить груз, то пружина сожмется на х₁ = 3 мм. На

сколько сожмет пружину тот же груз, упавший на конец пружины с высоты А = 8 см?

5. По горизонтальной плоскости катится диск со скоростью u = 8 м/с. Определить коэффициент сопротивления, если диск, будучи предоставленным самому себе, остановился, пройдя путь s = 18 м.

6. Однородный стержень длиной l=1,0 м может свободно вращать- ся вокруг горизонтальной оси, проходящей через один из его кон- цов. В другой конец абсолютно не упруго ударяет пуля массой т=7 г, летящая перпендикулярно стержню и его оси. Определить массу М стержня, если в результате попадания пули он отклонится на угол a =60°. Принять скорость пули u =360 м/с.

7. На каком расстоянии от центра Земли находится точка, в кото- рой напряженность суммарного гравитационного поля Земли и Луны равна нулю? Принять, что масса Земли в 81 раз больше массы Луны и что расстояние от центра Земли до центра Луны равно 60 радиусам Земли.

8. Определить период Т колебаний математического маятника, ес-

ли его модуль максимального перемещения Dr =18 см и макси-

мальная скорость

u_max =16 см/с.

Вариант 7

1. Материальная точка движется по окружности с постоянной уг-

ловой скоростью

w = p / 6

рад/с. Во сколько раз путь

Ds , пройденный

точкой за время t=4 с, будет больше модуля ее перемещения Dr ?

Принять, что в момент начала отсчета времени радиус-вектор r, за- дающий положение точки на окружности, относительно исходного

положения был повернут на угол j₀ = p /3 рад.

2. Снаряд, летевший со скоростью u = 400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса ко- торого составляет 40% от массы снаряда, полетел в противополож-

ном направлении со скоростью большего осколка.

u1 =150м/с. Определить скорость u2

3. Из ствола автоматического пистолета вылетела пуля массой

m₁ = 10 г со скоростью u = 300 м/с. Затвор пистолета массой m₂ =

200 г прижимается к стволу пружиной, жесткость которой k = 25 кН/м. На какое расстояние отойдет затвор после выстрела? Счи- тать, что пистолет жестко закреплен.

4. Из пружинного пистолета с пружиной жесткостью k= 150 Н/м был произведен выстрел пулей массой m= 8 г. Определить ско- рость u пули при вылете ее из пистолета, если пружина была сжата на х = 4 см.

5. Определить момент силы М, который необходимо приложить к блоку, вращающемуся с частотой п= 12с-1 , чтобы он остановился в

течение времени Dt = 8 с. Диаметр блока D= 30 см. Массу блока т

=6 кг считать равномерно распределенной по ободу.

6.

На краю платформы в виде диска, вращающейся по инерции вокруг вертикальной оси с частотой n =8 мин -1 , стоит человек мас- сой т 1 =70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой n₂=10 мин -1 . Определить массу m плат- формы. Момент инерции человека рассчитывать как для материаль- ной точки.

7. Спутник обращается вокруг Земли по круговой орбите на вы- соте h=520км. Определить период обращения спутника. Ускоре- ние свободного падения g у поверхности Земли и ее радиус R счи- тать известными.

8. Материальная точка совершает простые гармонические колеба- ния так, что в начальный момент времени смещение х₀=4 см, а скорость у₀=10 см/с. Определить амплитуду А и начальную фазу

j₀ колебаний, если их период Т=2 с.

Вариант 8

1. Материальная точка движется в плоскости ху согласно уравне-

ниям х= А + Вt + С t² и у= А + В t + С t² , где B =7 м/с, С ,= -2м/с², В₂= -

1м/с, С₂=0,2м/с². Найти модули скорости и ускорения точки в мо- мент времени t=5 с.

2. Две одинаковые лодки массами т = 200 кг каждая (вместе с че- ловеком и грузами, находящимися в лодках) движутся параллельными курсами навстречу друг другу с одинаковыми скоростями u = 1 м/с. Когда лодки поравнялись, то с первой лодки на вторую и со вто-

рой на первую одновременно перебрасывают грузы массами m₁ = 20

кг. Определить скорости

u1 и u2

лодок после перебрасывания грузов.

3. Шар массой

m₁ = 5 кг движется со скоростью

u₁ = 1 м/с и

сталкивается с покоящимся шаром массой m₂ = 2 кг. Определить

скорости u₁ и u 2 шаров после удара. Удар считать абсолютно упру-

гим, прямым, центральным.

4. Налетев на пружинный буфер, вагон массой т = 16 т, двигав- шийся со скоростью u = 0,6 м/с, остановился, сжав пружину на х = 8 см. Найти общую жесткость k пружин буфера.

5. Блок, имеющий форму диска массой т = 0,4 кг, вращается под действием силы натяжения нити, к концам которой подвешены гру-

зы массами m1 = 0,3 кг и m 2 = 0,7 кг. Определить силы натяжения Т1

и Т₂ нити по обе стороны блока.

6. На краю неподвижной скамьи Жуковского диаметром D=0,8 м

и массой m 1 =6 кг стоит человек массой т₂=60 кг. С какой угловой скоростью w начнет вращаться скамья, если человек поймает ле- тящий на него мяч массой m=0,5кг? Траектория мяча горизон- тальна и проходит на расстоянии r=0,4 м от оси скамьи. Скорость мяча u =5 м/с.

7. Определить линейную и угловую скорости спутника Земли, обращающегося по круговой орбите на высоте h=1000 км. Ускоре- ние свободного падения g у поверхности Земли и ее радиус R счи- тать известными.

8. Складываются два колебания одинакового направления и оди-

накового периода: х 1 =А 1 sinw₁ t

и х 2 =А₂ sinw₂ t

(t +t ), где А 1 = A₂ = 3

см, w = w 2 = pc^-1 , t =0,5с. Определить амплитуду А и начальную

фазу j₀ результирующего колебания. Написать его уравнение. По-

строить векторную диаграмму для момента времени t=0.

Вариант 9

1. Точка движется по окружности радиусом R = 4 м. Закон ее движения выражается уравнением S = А + Вt², где А = 8 м, В = -2 м/с². Определить момент времени, когда нормальное ускорение а_n точки равно 9 м/с². Найти скорость u, тангенциальное ускорение а_t и полное а ускорение точки в тот же момент времени t.

2. На сколько переместится относительно берега лодка длиной

l =3,5 м и массой m₁ = 200 кг, если стоящий на корме человек мас-

сой m₂ =80 кг переместится на нос лодки? Считать лодку располо-

женной перпендикулярно берегу.

3. Из орудия, не имеющего противооткатного устройства, произ- водилась стрельба в горизонтальном направлении. Когда орудие

было неподвижно закреплено, снаряд вылетел со скоростью u₁ =

600 м/с, а когда орудию дали возможность свободно откатываться

назад, снаряд вылетел со скоростью откатилось при этом орудие?

u₂ =580 м/с. С какой скоростью

4. Определить скорость поступательного движения сплошного ци- линдра, скатившегося с наклонной плоскости высотой 50 см.

5. К краю стола прикреплен блок. Через блок перекинута неве- сомая и нерастяжимая нить, к концам которой прикреплены грузы. Один груз движется по поверхности стола, а другой - вдоль вертика- ли вниз. Определить коэффициент f трения между поверхностями груза и стола, если массы каждого груза и масса блока одинаковы и грузы движутся с ускорением а = 5,6 м/с². Проскальзыванием нити по блоку и силой трения, действующей на блок, пренебречь.

6. Горизонтальная платформа массой m1 =150 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой п =8 мин -1 . Человек массой т₂=70 кг стоит при этом на краю платформы. С какой угловой скоростью w начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу круглым, однородным диском, а человека - ма- териальной точкой.

7. Какова масса Земли, если известно, что Луна в течение года со- вершает 13 обращений вокруг Земли и расстояние от Земли до Луны равно 3,84∙10⁸м?

8. На гладком горизонтальном столе лежит шар массой М=200 г, прикрепленный к горизонтально расположенной легкой пружине с жесткостью k= 500 Н/м. В шар попадает пуля массой т=10 г, ле- тящая со скоростью u =300 м/с, и застревает в нем. Пренебрегая перемещением шара во время удара и сопротивлением воздуха, определить амплитуду А и период Т колебаний шара.

КОНТРОЛЬНАЯ РАБОТА № 2

Вариант 0

1. Определить количество вещества n и число N молекул азота массой т=0,2кг.

2. Определить плотность r водяного пара, находящегося под давлением р=2,5кПа и имеющего температуру Т =250 К.

3. Определить среднюю кинетическую энергию e _П поступатель-

ного движения и

e вр

вращательного движения молекулы азота при

температуре Т=1кК. Определить также полную кинетическую энер- гию Е_к молекулы при тех же условиях.

4. Одноатомный газ при нормальных условиях занимает объем

V=5л. Вычислить теплоемкость СV этого газа при постоянном объе- ме.

5. В сферической колбе вместимостью V= 3л, содержащей азот, со- здан вакуум с давлением р= 80 мкПа. Температура газа Т = 250 К. Можно ли считать вакуум в колбе высоким?'

Примечание. Вакуум считается высоким, если длина свободного пробега молекул в нем много больше линейных размеров сосуда.

6. Определить работу А, которую совершит азот, если ему при по- стоянном давлении сообщить количество теплоты Q=21 кДж. Найти

также изменение DU внутренней энергии газа.

7. В цикле Карно газ получил от теплоотдатчика теплоту Q 1 = 500Дж и совершил работу A= 100Дж. Температура теплоотдатчика T 1 = 400 К. Определить температуру T₂ теплоприемника.

8. Две капли ртути радиусом r=1,2 мм каждая слились в одну большую каплю. Определить энергию Е, которая выделится при этом слиянии. Считать процесс изотермическим.

Вариант 1

1. Определить количество вещества n и число N молекул кисло- рода массой т = 0,5 кг.

2. В цилиндр длиной l=1,6м, заполненный воздухом при нормаль- ном атмосферном давлении р₀, начали медленно вдвигать поршень площадью основания S= 200 см². Определить силу F, действующую на поршень, если его остановить на расстоянии l 1 = 10 см от дна цилиндра.

3. Определить внутреннюю энергию U водорода, а также среднюю кинетическую энергию e молекулы этого газа при температуре T= 300 К, если количество вещества n этого газа равно 0,5 моль.

4. Определить молярную массу М двухатомного газа и его удель-

ные теплоемкости, если известно, что разность лоемкостей этого газа равна 260 Дж/(кг×К).

с р - с V

удельных теп-

5. Найти среднее число z столкновений за время t= 1 с и длину свободного пробега (l) молекулы гелия, если газ находится под дав- лением р= 2кПа при температуре T= 200 К.

6. Определить количество теплоты Q, которое надо сообщить кис- лороду объемом V= 50 л при его изохорном нагревании, чтобы давле-

ние газа повысилось на Dр = 0,5 МПа.

7. Идеальный газ совершает цикл Карно при температурах тепло- приемника T₂=290К и теплоотдатчика Т 1 = 400 К. Во сколько раз уве- личится коэффициент полезного действия h цикла, если температура

теплоотдатчика возрастет до Т₁¢ =600 К?

8. Найти массу т воды, вошедшей в стеклянную трубку с диамет- ром канала d=0,8 мм, опущенную в воду на малую глубину. Считать смачивание полным.

Вариант 2

1. Сколько атомов содержится в ртути: 1) количеством веще- ства n =0,2моль; 2) массой т=1 г?

2. В баллоне находится газ при температуре Т 1 = 400 К. До ка- кой температуры Т₂ надо нагреть газ, чтобы его давление увеличи- лось в 1,5 раза?

3. Определить суммарную кинетическую энергию Е_к поступатель- ного движения всех молекул газа, находящегося в сосуде вмести- мостью V=3л под давлением р = 540 кПа.

4. Найти удельные c p

углекислого газа.

и с V , а также молярные С _р и С V теплоемкости

5. Определить среднюю длину свободного пробега l молекулы азота в сосуде вместимостью V= 5л. Масса газа т= 0,5 г.

6. При изотермическом расширении азота при температуре Т = 280 К объем его увеличился в два раза. Определить: 1) совершенную при

расширении газа работу A; 2) изменение DU внутренней энергии; 3)

количество теплоты Q, полученное газом. Масса азота т= 0,2 кг.

7. Идеальный газ совершает цикл Карно. Температура Т 1 теплоот- датчика в четыре раза (n=4) больше температуры теплоприемника. Какую долю w количества теплоты, полученного за один цикл от теплоотдатчика, газ отдаст теплоприемнику?

8. Какую работу А надо совершить при выдувании мыльного пузы-

3 3

ря, чтобы увеличить его объем от V1 = 8 см до V =16см ? Считать

процесс изотермическим.

Вариант 3

1. Вода при температуре t= 4°С занимает объем V= 1 см³. Опре- делить количество вещества V и число N молекул воды.

2. Баллон вместимостью V= 20 л заполнен азотом при температу- ре T=400К. Когда часть газа израсходовали, давление в баллоне

понизилось на Dp =200кПа. Определить массу т израсходованного

газа. Процесс считать изотермическим.

3. Количество вещества гелия n = 1,5 моль, температура T=120К. Определить суммарную кинетическую энергию E_к поступательного движения всех молекул этого газа.

4. Определить показатель адиабаты g идеального газа, который при температуре Т = 350 К и давлении р= 0,4МПа занимает объем V=

300л и имеет теплоемкость С V =857 Дж/К.

5. Водород находится под давлением р= 20 мкПа и имеет темпера- туру T=300К. Определить среднюю длину свободного пробега l мо- лекулы такого газа.

6. При адиабатном сжатии давление воздуха было увеличено от р1 = 50кПа до р 2 = 0,5МПа. Затем при неизменном объеме температура

воздуха была понижена до первоначальной. Определить давление p 3

газа в конце процесса.

7. Определить работу A₂ изотермического сжатия газа, совершаю-

щего цикл Карно, КПД которого h = 0,4, если работа изотермического расширения равна А1 =8 Дж.

8. Какая энергия Е выделится при слиянии двух капель ртути диа- метром d 1 =0,8мм и d 2 = 1,2 мм в одну каплю?

Вариант 4

1. Найти молярную массу М и массу т М одной молекулы пова- ренной соли.

2. В баллоне вместимостью V=15 л находится аргон под давлени-

ем p₁ =600кПа и при температуре T₁ = 300 К. Когда из баллона было

взято некоторое количество газа, давление в баллоне понизилось до р₂=400кПа, а температура установилась Т₂ = 260К. Определить мас- су т аргона, взятого из баллона.

3. Молярная внутренняя энергия U_т некоторого двухатомного газа равна 6,02кДж/моль. Определить среднюю кинетическую энергию

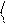eвр

вращательного движения одной молекулы этого газа. Газ счи-

тать идеальным.

4. В сосуде вместимостью V=6л находится при нормальных усло- виях двухатомный газ. Определить теплоемкость С V этого газа при постоянном объеме.

5. При нормальных условиях длина свободного пробега l молеку- лы водорода равна 0,160 мкм. Определить диаметр d. молекулы водо- рода.

6. Кислород массой т = 200г занимает объем V1 = 100 л и находит- ся под давлением р1 = 200кПа. При нагревании газ расширился при постоянном давлении до объема V 2 = 300л, а затем его давление воз-

росло до р 3 =500кПа при неизменном объеме. Найти изменение внут-

ренней энергии DU газа, совершенную газом работу A и теплоту Q,

переданную газу. Построить график процесса.

7. Газ, совершающий цикл Карно, отдал теплоприемнику теплоту Q₂= 14 кДж. Определить температуру Т1 теплоотдатчика, если при температуре теплоприемника T₂ = 280К работа цикла A = 6кДж.

8. Определить давление р внутри воздушного пузырька диаметром d= 4 мм, находящегося в воде у самой ее поверхности. Считать атмо- сферное давление нормальным.

Вариант 5

1. Определить массу m_м одной молекулы углекислого газа.

2. Два сосуда одинакового объема содержат кислород. В одном

сосуде давление

p₁ = 2МПа и температура

T₁ = 800 К, в другом р₂ =

2,5МПа, T₂ = 200К. Сосуды соединили трубкой и охладили находя- щийся в них кислород до температуры Т=200К. Определить уста- новившееся в сосудах давление р.

3. Определить среднюю кинетическую энергию e одной молеку- лы водяного пара при температуре Т=500 К.

4. Определить относительную молекулярную массу М r и молярную

массу М газа, если разность его удельных теплоемкостей кДж/ (кг × К).

c p - c V = 2,08

5. Какова средняя арифметическая скорость u молекул кислорода при нормальных условиях, если известно, что средняя длина свобод- ного пробега l молекулы кислорода при этих условиях равна 100 нм?

6. Объем водорода при изотермическом расширении при темпера- туре Т=300К увеличился в n = 3 раза. Определить работу А, совер-

шенную газом, и теплоту полученную при этом. Масса m водорода равна 200 г.

7. Газ, являясь рабочим веществом в цикле Карно, получил от теп- лоотдатчика теплоту Q1 = 4,38кДж и совершил работу А = 2,4 кДж. Определить температуру теплоотдатчика, если температура тепло-

приемника Т ₂ = 273 К.

8. Пространство между двумя стеклянными параллельными пла- стинками с площадью поверхности S= 100 см² каждая, расположен- ными на расстоянии l=20мкм друг от друга, заполнено водой. Опре- делить силу F прижимающую пластинки друг к другу. Считать ме- ниск вогнутым с диаметром d, равным расстоянию между пластинка- ми.

Вариант 6

1. Определить концентрацию п молекул кислорода, находящего- ся в сосуде вместимостью V=2л. Количество вещества n кислоро- да равно 0,2 моль.

2. Вычислить плотность r азота, находящегося в баллоне под давлением р=2МПа и имеющего температуру Т = 400 К.

3. Определить среднюю квадратичную скорость

uкв

молекулы газа,

заключенного в сосуд вместимостью V=2 л под давлением р = 200 кПа. Масса газа т = 0,3 г.

4. Определить молярные теплоемкости газа, если его удельные теп-

лоемкости

с V = 10,4 кДж/(кг×К) и

c p = 14,6 кДж/(кг×К).

5. Кислород находится под давлением р=133 нПа при температуре Т= 200 К. Вычислить среднее число z столкновений молекулы кис- лорода при этих условиях за время t = 1 с.

6. Азот массой т = 0,1 кг был изобарно нагрет от температуры Т 1 =

200 К до температуры T₂ = 400 К. Определить работу А, совершенную

газом, полученную им теплоту Q и изменение DU

азота.

внутренней энергии

7. Газ, совершающий цикл Карно, отдал теплоприемнику 67% теп-

лоты, полученной от теплоотдатчика. Определить температуру T₂

теплоприемника, если температура теплоотдатчика T₁ = 430 К.

8. Глицерин поднялся в капиллярной трубке диаметром канала d=1 мм на высоту h= 20 мм. Определить поверхностное натяжение a гли- церина. Считать смачивание полным.

Вариант 7

1. Определить количество вещества n водорода, заполняющего сосуд объемом V=3 л, если концентрация молекул газа в сосуде n= 2×10¹⁸ м -3 .

2. Определить относительную молекулярную массу М_r газа, если при температуре Т=154 К и давлении р=2,8МПа он имеет плот- ность r =6,1кг/м³.

3. Водород находится при температуре T= 300 К. Найти среднюю

кинетическую энергию

eвр

вращательного движения одной молеку-

лы, а также суммарную кинетическую энергию Е к всех молекул это- го газа; количество водорода v= 0,5 моль.

4. Найти удельные с V

гелия.

и c p

и молярные C V

и C p

теплоемкости азота и

5. При каком давлении р средняя длина свободного пробега l мо- лекул азота равна 1 м, если температура газа t=10°С?

6. Во сколько раз увеличится объем водорода, содержащий количе- ство вещества n = 0,4 моль при изотермическом расширении, если при этом газ получит количество теплоты Q= 800Дж? Температура водо- рода T= 300 К.

7. Во сколько раз увеличится коэффициент полезного действия h

цикла Карно при повышении температуры теплоотдатчика от T1 = 380

К до

Т1¢ = 560 К? Температура теплоприемника

Т ₂ = 280 К.

8. В воду опущена на очень малую глубину стеклянная трубка с диаметром канала d= 1 мм. Определить массу т воды, вошедшей в трубку.

Вариант 8

1. В баллоне вместимостью V=3л содержится кислород массой

т=10г. Определить концентрацию п молекул газа.

2. Найти плотность r азота при температуре T=400 К и давле- нии р=2МПа.

3. При какой температуре средняя кинетическая энергия e_п

ступательного движения молекулы газа равна 4,14×10 -21 Дж?

по-

4. Вычислить удельные теплоемкости газа, зная, что его молярная

масса М=4×10 -3

кг/моль и отношение теплоемкостей

С / С

=1,67.

р V

5. В сосуде вместимостью V=5л находится водород массой т = 0,5 г. Определить среднюю длину свободного пробега l молекулы во- дорода в этом сосуде.

6. Какая работа А совершается при изотермическом расширении водорода массой т = 5г, взятого при температуре T= 290 К, если объ- ем газа увеличивается в три раза?

7. Идеальная тепловая машина работает по циклу Карно. Темпера-

тура теплоотдатчика

Т₁ = 500 К, температура теплоприемника

Т 2 =

250К. Определить КПД h цикла, а также работу А1 рабочего вещества при изотермическом расширении, если при изотермическом сжатии

совершена работа А₂ = 70 Дж.

8. На сколько давление р воздуха внутри мыльного пузыря больше нормального атмосферного давления р₀, если диаметр пузыря d=5 мм?

Вариант 9

1. Определить относительную молекулярную массу М r : 1) воды; 2) углекислого газа; 3) поваренной соли.

2. В сосуде вместимостью V=40 л находится кислород при темпе- ратуре Т=300К. Когда часть газа израсходовали, давление в бал-

лоне понизилось на Dp = 100 кПа. Определить массу т израсходо-

ванного кислорода. Процесс считать изотермическим.

3. В азоте взвешены мельчайшие пылинки, которые движутся так, как если бы они были очень крупными молекулами. Масса каждой пылинки равна 6×10 -10 г. Газ находится при температуре Т= 400 К.

Определить средние квадратичные скорости

uкв

, а также средние

кинетические энергии e_п

и пылинки.

поступательного движения молекулы азота

4. Трехатомный газ под давлением р = 240кПа и температуре t=

20°С занимает объем V=10л. Определить теплоемкость С р

при постоянном давлении.

этого газа

5. Средняя длина свободного пробега l молекулы водорода при некоторых условиях равна 2 мм. Найти плотность р водорода при этих условиях.

6. Какая доля w₁ количества теплоты Q, подводимого к идеальному

двухатомному газу при изобарном процессе, расходуется на увеличе-

ние DU

внутренней энергии газа и какая доля w ₂

на работу А расши-

рения? Рассмотреть три случая, если газ: 1) одноатомный; 2) двух- атомный; 3) трехатомный.

7. Газ, совершающий цикл Карно, получает теплоту Q1 = 84кДж. Определить работу А газа, если температура Т1 теплоотдатчика в три

раза выше температуры T₂ теплоприемника.

8. Воздушный пузырек диаметром d= 2,2 мкм находится в воде у самой ее поверхности. Определить плотность r воздуха в пузырьке, если воздух над поверхностью воды находится при нормальных условиях.