Тема: Объем геометрических тел

Тема: Объем геометрических тел
Вариант 1
1. Во сколько раз увеличится объем куба, если его ребра увеличить в 4 раза?
2. Объем одного куба в 64 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

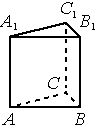
3. Найдите объём многогранника, вершинами которого являются точки A, B, C , C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 6, а боковое ребро равно 9.
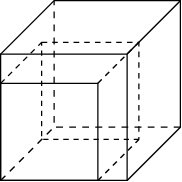
4. Найдите объём многогранника, изображённого на рисунке (все двугранные углы – прямые).

5. Найдите объём многогранника, вершинами которого являются точки A, B, C , A 1 , B1, C1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 12, а боковое ребро равно 12.
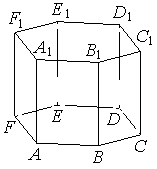
6. Найдите объём многогранника, вершинами которого являются вершины A, B, C, D, E, F, D 1, правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1 , площадь основания которой равна 3, а боковое ребро равно 9.

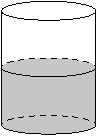
7. В цилиндрическом сосуде уровень жидкости достигает 192 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 8 раз больше диаметра первого? Ответ выразите в сантиметрах.
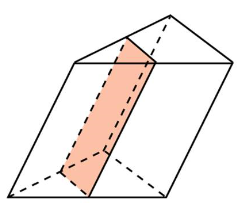
8. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсеченной треугольной призмы равен 3,5.
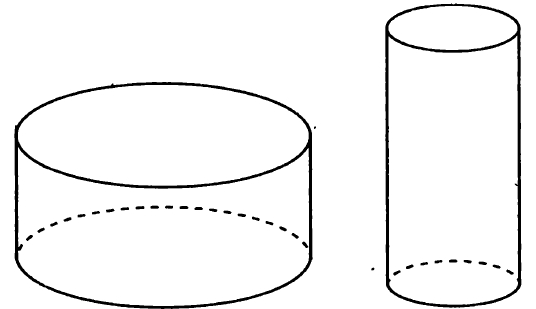
9. Объем первого цилиндра равен 18 м3. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
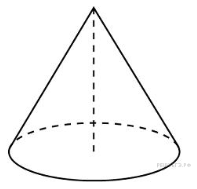
10. Во сколько раз увеличится объём конуса, если радиус его основания увеличить в 6 раз, а высоту оставить прежней?

11. Первая цилиндрическая кружка вдвое выше второй, зато вторая в шесть раз шире. Найдите отношение объёма второй кружки к объёму первой.
12. Во сколько раз увеличится объем шара, если его радиус увеличить в шесть раз?
13. От треугольной пирамиды, объем которой равен 24, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
14. В правильной четырёхугольной пирамиде высота равна 5, боковое ребро равно 7. Найдите её объём.
15. В цилиндрический сосуд, в котором находится 10 дм3 воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 1,6 раза. Чему равен объём детали? Ответ выразите в дм3.


Тема: Объем геометрических тел
Вариант 2
1. Объем куба равен 512. Найдите площадь его поверхности.
2. Найдите объём многогранника, вершинами которого являются точки A, B, C , C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 6, а боковое ребро равно 3.

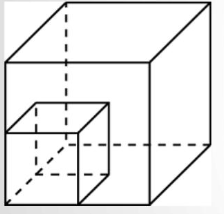
3. Найдите объём многогранника, изображённого на рисунке (все двугранные углы – прямые).

4. Площадь грани прямоугольного параллелепипеда равна 2. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
5. Найдите объём многогранника, вершинами которого являются точки A, E , F , A 1 , E1, F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 12, а боковое ребро равно 13.

6. Найдите объём многогранника, вершинами которого являются вершины A, B, C, D, E, F, D 1, правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1 , площадь основания которой равна 5, а боковое ребро равно 9.

7. В цилиндрическом сосуде уровень жидкости достигает 294 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 7 раз больше диаметра первого? Ответ выразите в сантиметрах.

8. Через среднюю линию основания треугольной призмы, объем которой равен 52, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.

9. Объем первого цилиндра равен 24 м3. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.

10. В сосуде, имеющем форму конуса, уровень жидкости достигает  высоты. Объём жидкости равен 144 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
высоты. Объём жидкости равен 144 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

11. В цилиндрический сосуд, в котором находится 10 дм3 воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 1,6 раза. Чему равен объём детали? Ответ выразите в дм3.

12. Первая цилиндрическая кружка вдвое выше второй, зато вторая в пять раз шире. Найдите отношение объёма второй кружки к объёму первой.
13. Во сколько раз увеличится объем шара, если его радиус увеличить в четыре раза?

14. От треугольной пирамиды, объем которой равен 36, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

15. В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 4. Найдите её объём.

ОТВЕТЫ
| Вариант 1 | Вариант 2 |
| 64 | 384 |
| 16 | 6 |
| 18 | 28 |
| 24 | 8 |
| 24 | 26 |
| 9 | 15 |
| 3 | 6 |
| 14 | 13 |
| 13,5 | 18 |
| 36 | 180 |
| 18 | 6 |
| 216 | 12,5 |
| 6 | 64 |
| 80 | 9 |
| 6 | 16 |








