Задание на контрольную работу № 1
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ ЗАДАЧ №№1-10
Первые десять задач посвящены практическому использованию конденсаторов как статических элементов для накапливания электрических зарядов. По учебнику [1] следует проработать главу 2 «Электрическая емкость и конденсаторы».
Конденсаторы в основном различаются двумя параметрами: емкостью и допустимым напряжением.
Емкость показывает, какое количество зарядов может накопить тот или иной конденсатор при увеличении напряжения на его обкладках на один вольт. Емкость не зависит от приложенного от напряжения, а зависит от площади обкладки, расстояния между обкладками и диэлектрической проницаемости среды между ними.
Конденсаторы могут соединяться параллельно. Когда необходимо увеличить общую емкость схемы. Ее емкость будет равна сумме емкостей конденсаторов. Соединенных параллельно.
При последовательном соединении конденсаторов их общая емкость будет меньше емкости конденсатора, обладающего самой малой емкостью. Заряд на каждом конденсаторе одинаков, а напряжение на обкладках будет у того конденсатора больше, у которого меньше емкость. Подсчет эквивалентной емкости производится по формуле:
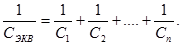
Такое соединение конденсаторов применяется, как правило, в тех случаях, когда напряжение источника больше рабочего напряжения (UРАБ) отдельного конденсатора. Например, напряжение сети U=400B,а конденсатор рассчитан на UРАБ=200В. Тогда путем последовательного соединения двух таких конденсаторов решается проблема. Чтобы найти общий заряд, необходимо найти величину эквивалентной емкости заданной схемы. Для этого нужно постепенно «свертывать» схему, т.е. заменять последовательно (или параллельно) соединенную группу конденсаторов одним конденсатором, предварительно вычислив его емкость.
Пример 1
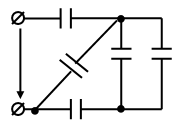
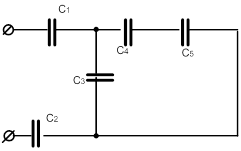
На рисунке приведена схема соединения конденсаторов. Ёмкости заданы в мкФ: С1=50 мкФ, С2=С5=30 мкФ, С3=25 мкФ, С4=35 мкФ. Напряжение сети U=100 В.
Вычислить эквивалентную ёмкость и общий заряд батареи, напряжение на каждом конденсаторе и энергию, накопленную батареей.
 Краткая запись условия С1
Краткая запись условия С1
Дано: С1=50 мкФ
С2=С5=30 мкФ
С3=25 мкФ С3 С4
С4=35 мкФ С2
U=100 В
Определить: CЭКВ, QОБЩ, U1,
U2, U3, U4, U5, С5
Рис.1
Решение
1)Эквивалентная ёмкость батареи СЭКВ определяется методом свёртывания схемы:
Конденсаторы С3 и С4 соединены параллельно, их общая ёмкость: С34= С3 + С4 = 25 + 35 = 60 мкФ;
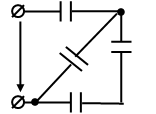 2)Схема приобретает вид, представленный на следующем рисунке:
2)Схема приобретает вид, представленный на следующем рисунке:
С34
С2
С5
Рис.2
Конденсаторы С34 и С5 соединены последовательно, их общая ёмкость :
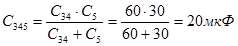
3)Схема приобретает вид:
 C1
C1
C345
C2
Рис.3
Конденсаторы С2 и С345 соединены параллельно, их общая ёмкость :
С2345 = С2 + С345 = 30 + 20 = 50 мкФ;
4)После всех преобразований схема принимает простой вид:
 C1
C1
C2-5
Рис.4
Конденсаторы С1 и С2345 соединены последовательно. Поэтому эквивалентная ёмкость батареи :
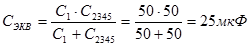

5)Общий заряд батареи:
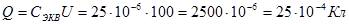
6) Напряжение на каждом конденсаторе:
а) Так как QОБЩ = Q1 = Q2345, то
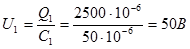
б)Напряжение на батарее конденсаторов С2345:
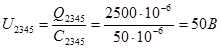
U2345 = U2 = U345 , т.к. соединение параллельное
U2 = 50 B
U345 = 50 B

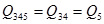
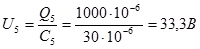
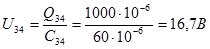
U3 = U4, U3=16,7 В, U4=16,7 В
Задачи №№1 -10
На рисунке, соответствующем номеру задачи, изображена схема соединения конденсаторов, емкости которых, а также приложенное напряжение, заданы в таблице .
Вычертите схему, соблюдая размеры элементов согласно ГОСТу. Определите эквивалентную емкость и общий заряд при заданном напряжении,
Таблица
| Номер задачи | Ед. изм. | С1 | С2 | С3 | С4 | С5 | U ,В |
| 1 | мкФ | 20 | 40 | 30 | 20 | 20 | 100 |
| 2 | мкФ | 200 | 400 | 300 | 200 | 200 | 10 |
| 3 | мкФ | 50 | 100 | 80 | 40 | 40 | 50 |
| 4 | мкФ | 100 | 200 | 150 | 100 | 100 | 100 |
| 5 | мкФ | 200 | 400 | 150 | 500 | 500 | 150 |
| 6 | мкФ | 25 | 50 | 30 | 40 | 40 | 100 |
| 7 | мкФ | 20 | 40 | 25 | 30 | 30 | 50 |
| 8 | мкФ | 300 | 600 | 350 | 500 | 500 | 50 |
| 9 | мкФ | 25 | 50 | 30 | 40 | 40 | 100 |
| 10 | мкФ | 200 | 400 | 300 | 200 | 200 | 10 |
| Номер задачи | Схема |
| 1 |
|
| 2 | 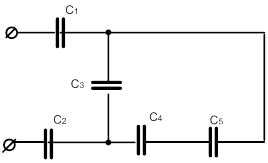
|
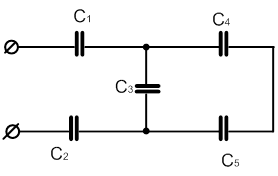
| 3 |
|
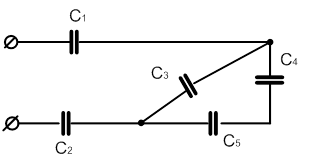
| 4 |
|
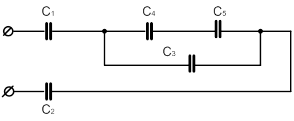
| 5 |
|
| 6 | 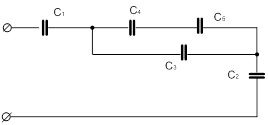
|
| 7 |
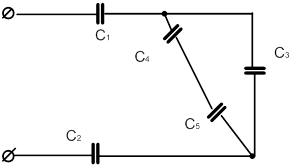
|
| 8 |
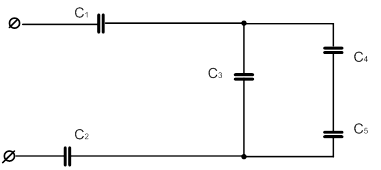
|
| 9 |
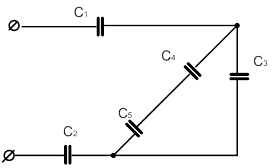
|
| 10 | 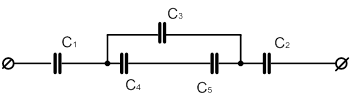
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ ЗАДАЧ №№11-20
Задачи №№11-20 посвящены теме «Расчет простых электрических цепей постоянного тока», которые решаются при помощи законов Ома. Проверку правильности отдельных этапов решения можно сделать по первому закону Кирхгофа. По учебнику [1] следует проработать главу 4 «Простые электрические цепи постоянного тока».
При последовательном соединении резисторов их сопротивления складываются, т.е. 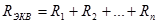 .
.
Т.к. токи в последовательно соединенных резисторах одинаковы, то падение напряжения будет больше на том резисторе, у которого сопротивление больше.
При параллельном соединении резисторов их общее (эквивалентное) сопротивление будет меньше сопротивления резистора, имеющего самое малое его значение.
Обычно находят общую проводимость
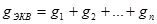 ,
,
где
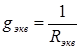
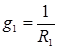
При решении данных задач необходимо применять метод. «свертывания» цепи, т. е. заменять группу последовательно (или параллельно) соединенных резисторов одним резистором, имеющим эквивалентное сопротивление, всякий раз вычерчивая заново упрощенную схему. В конце концов схема будет «свернута» до одного резистора, имеющего
сопротивление R ЭКВ .
Все резисторы помимо сопротивления характеризуются также допустимой мощностью теплового рассеивания. Дело в том, что конструкция и материал каждого резистора рассчитаны на определенную мощность, выделяемую в виде тепла.
При увеличении мощности выше допустимой резистор может разрушиться. Поэтому резисторы подбираются также по допустимой мощности теплового рассеивания.
Чтобы найти ее значение для каждого резистора, входящего в схему, необходимо определить величину тока в каждом из них. Тогда 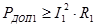 и так для каждого из резисторов.
и так для каждого из резисторов.
Далее необходимо снова рассчитать схему в измененных условиях (замыкание контакта P 1или P 2). Схема несколько упрощается. Важно уяснить, как изменение в одной части схемы влияет на состояние всех других ее частей.
Непосредственно перед решением задач следует разобрать пример .
Пример
Цепь постоянного тока, схема которой приведена на рис1.2.5., состоит из пяти резисторов, сопротивления которых равны: R1=4 Ом, R2=12 Ом, R3=12 Ом, R4=6 Ом, R5=4 Ом напряжение, приложенное к цепи, U=20 В.
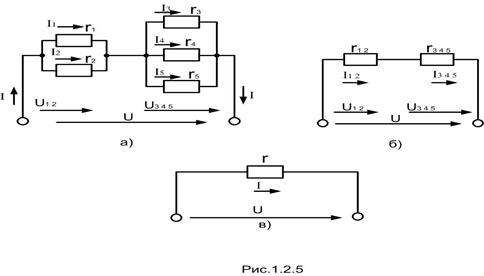
Определить эквивалентное сопротивление всей цепи Rэкв., мощность, потребляемую цепью, P и токи, проходящие через каждый резистор: I1, I2, I3, I4, I5.
Ход решения:
1.Обозначим стрелками токи, проходящие через каждый резистор.
2.Определим эквивалентное сопротивление цепи:
а) т.к. R1 и R2 соединены параллельно, то
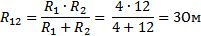
б) т.к. R 3, R4, R5 соединены параллельно, то
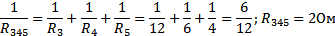
в) Эквивалентное сопротивление:
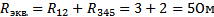
3.Ток в цепи:
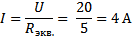
4. Мощность, потребляемая цепью:
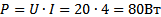
5. Токи, проходящие через каждый резистор:
а) 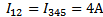 , т.к. соединение на участках с этими сопротивлениями последовательное.
, т.к. соединение на участках с этими сопротивлениями последовательное.
б) токи в сопротивлениях R3 и R4 найдем по закону Ома, где
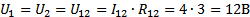
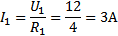
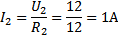
б) токи в сопротивлениях R3, R4, R5 найдем по закону Ома, где
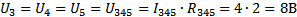
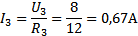
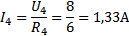
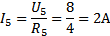
Задачи №11-20.
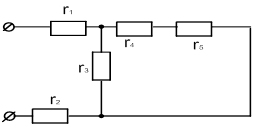
Для каждой схемы даны сопротивления резисторов r 1 , r 2 , r 3 , r 4 , r 5 и напряжение источника питания U . Определить эквивалентное сопротивление цепи R ЭКВ. , общий ток цепи I , а также токи каждого резистора I 1 , I 2 , I 3 , I 4 , I 5.
| Номер задачи | Ед. изм. | r 1 | r 2 | r 3 | r4 | r 5 | U ,В |
| 11 | Ом | 2 | 8 | 10 | 3 | 7 | 100 |
| 12 | Ом | 50 | 20 | 60 | 20 | 40 | 500 |
| 13 | Ом | 15 | 20 | 10 | 4 | 6 | 80 |
| 14 | Ом | 10 | 25 | 30 | 20 | 10 | 250 |
| 15 | Ом | 60 | 40 | 200 | 150 | 50 | 600 |
| 16 | Ом | 10 | 3 | 14 | 10 | 4 | 20 |
| 17 | Ом | 4 | 2 | 8 | 5 | 3 | 60 |
| 18 | Ом | 10 | 4 | 12 | 7 | 5 | 80 |
| 19 | Ом | 20 | 15 | 70 | 30 | 40 | 140 |
| 20 | Ом | 10 | 25 | 50 | 30 | 20 | 240 |
| Номер задачи | Схема |
| 11 |
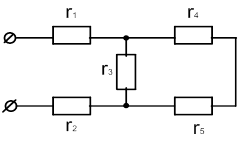
|
| 12 |
|
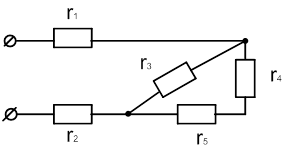
| 13 |
|
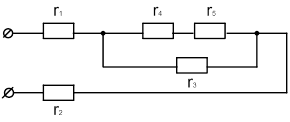
| 14 | 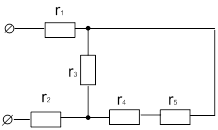
|
| 15 |
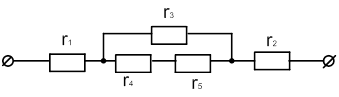
|
| 16 |
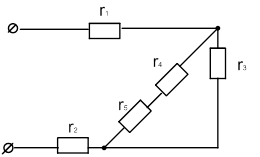
|
| 17 |
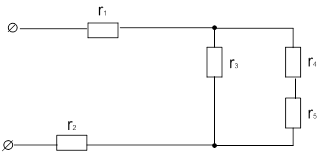
|
| 18 |
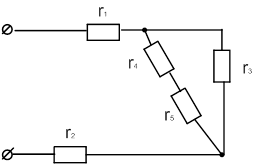
|
| 19 |
|
| 20 |
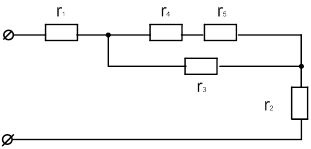
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ ЗАДАЧ №№21-30
Задачи №№21-30 посвящены теме «Расчет сложных электрических цепей постоянного тока», которые решаются при помощи законов Ома и Кирхгофа. По учебнику [1] следует проработать главу «Сложные электрические цепи постоянного тока».
Сложной называется разветвленная цепь с несколькими источниками электроэнергии в разных параллельных ветвях.
В сложных цепях источники эдс могут располагаться в ветвях произвольно в любом количестве и с произвольным выбором полярности подключения.
Нужно, прежде всего, усвоить, что означают такие понятия как узел, ветвь, контур. Необходимо также четкое понимание первого и второго законов Кирхгофа и умение их применять при расчете сложных цепей. Затем приступайте к разбору и усвоению метода узловых потенциалов.
При расчете сложных цепей чаще всего приходится определять токи в ветвях по заданным ЭДС и сопротивлениям ветвей. Для этой цели рекомендуется следующий порядок решения этих задач:
а) составляется электрическая схема цепи;
б) подсчитывается число неизвестных токов (ветвей) и устанавливаются для них произвольные направления;
в)определяются проводимости ветвей;;
г) определяются токи в ветвях с учетом направлений ЭДС и узлового напряжения.
Если в результате решения системы уравнений получаются отрицательные значения токов каких-либо ветвей, то это означает, что действительные направления токов в этих ветвях противоположны выбранным.
Непосредственно перед решением задач следует разобрать пример .
Пример
На заданном рисунке изображена схема сложной электрической цепи. ЭДС источника энергии Е1=180 В, Е2=96В, их внутренние сопротивления R01=R02=0,8 Ом, сопротивления резисторов R1=9,2 Ом, R2=19,2 Ом, R3=25 Ом. Определить токи I1,I2,I3, в ветвях цепи методом узловых и контурных уравнений.
Проверить решение методом узлового напряжения. Составить уравнение баланса мощностей.
 Краткая запись условия
Краткая запись условия
Дано: Е1=180 В А
Е2=96В
R01=R02=0,8 Ом Е1,R01 Е2,R02
R1=9,2 Ом - -
R2=19,2 Ом
R3=25 Ом. R1 R3 R2
I1 I3 I2
Определить : I1,I2,I3
В
Решение
1) Определяем проводимости ветвей по формулам:
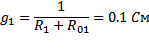
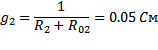
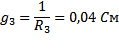
2) Определяем узловое напряжение по формуле:
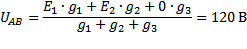
В данной формуле в знаменателе всегда пишется сумма проводимостей всей ветвей, а в числителе - сумма, в которой каждое слагаемое – это произведение ЭДС источника данной ветви на проводимость этой же ветви. Если ЭДС направлена к точке высшего потенциала (в нашем случае вверх), то она берется с плюсом, если вниз – с минусом.
3) Определяем токи в ветвях по формулам:
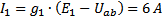
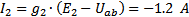
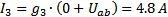
Ток I2 получился отрицательным, значит, первоначально указанное направление этого тока на заданной схеме было неверным, его надо изменить на противоположное.
Задача №21
 | |||
| |||
Задача №22
|
 |
Задача №23
| |||
 | |||
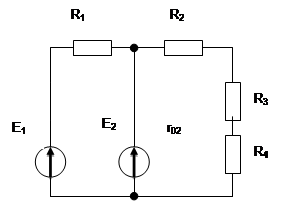 Задача №24
Задача №24
| |||
| |||
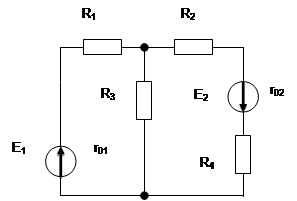 Задача №25
Задача №25
|
Задача №26
|
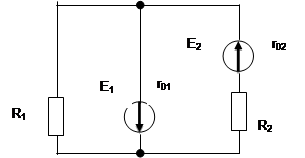 |
Задача №27
| |||
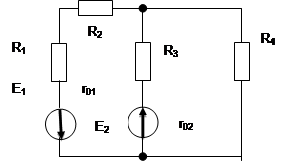 | |||
Задача №28
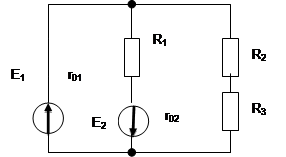
|
Задача №29
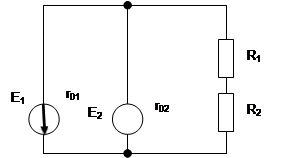
|
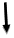 |
Задача №30
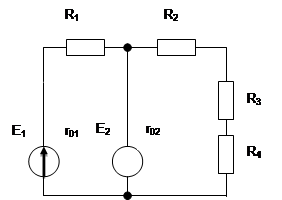 |
|
 |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ ЗАДАЧ №№31-40
Задачи №№31-430 посвящены расчету неразветвленных цепей однофазного переменного тока.
Процессы, протекающие в цепях переменного тока, являются более сложными по сравнению с процессами в цепях постоянного тока. Прежде всего, надо усвоить основные понятия о переменном токе.
Переменным называется ток, направление и значение которого периодически меняются.
Время Т, в течение которого переменный ток совершает полный цикл изменений, называется периодом переменного тока, а число периодов в секунду - его частотой:
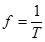
Единицей частоты является герц [Гц].
Наиболее распространен синусоидальный ток (напряжение, ЭДС).
Уравнения синусоидальных тока и напряжения:
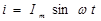
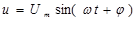
где i , u - мгновенные значения тока и напряжения (в любой
момент времени); Im, Um - максимальные значения тока и напряжения (амплитуды);
w - угловая частота, рад/с;
(wt+j) - фаза, т.е. угол, определяющий значение переменной величины в любой момент времени(текущая фаза);
j - начальная фаза переменной величины, т.е. угол, определяющий ее значение при t=0.
Приборы (амперметр, вольтметр), включенные в цепь переменного тока, показывают действующие значения величин (тока, напряжения), которые равны: 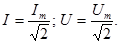
Цепи переменного тока (как и цепи постоянного тока) могут быть неразветвленными и разветвленными.
Прежде чем приступать к расчету цепей переменного тока, содержащих несколько элементов, надо запомнить свойства простейших цепей (таблица.9) :
а) с сопротивлением R;
б) с индуктивностью L;
в) с емкостью С.
Таблица 9
| Основные понятия | Активное Сопротивление | Индуктивное сопротивление | Емкостное сопротивление |
| Схема цепи |

|
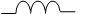
|
|
| Сопротивление | 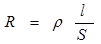
|
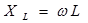
| 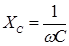
|
| Закон Ома для действующих значений | 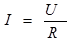
| 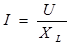
| 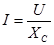
|
| Векторные диаграммы |
 U I U I
| 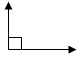 U
I U
I
| 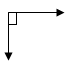 I
U I
U
|
| Уравнения тока и напряжения | 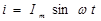
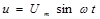
| 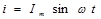
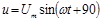
| 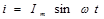
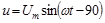
|
| Волновые диаграммы |  
|    
| 
|
| Мощность цепи | Активная
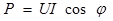
| Реактивная
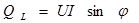
| Реактивная
|
Расчет цепи переменного тока облегчается, если использовать построение векторной диаграммы, на которой изображается несколько синусоидальных величин одной частоты.
1.Построение векторной диаграммы начинают с вектора величины.
Общей для всей цепи, т.е. вектора тока в неразветвленной цепи. Этот вектор строят в положительном направлении оси абсцисс (горизонтально вправо).
2.Длины векторов в масштабе соответствуют действующим значениям величин.
3.Положение каждого вектора на диаграмме определяется начальной фазой. Причем опережение по фазе – против часовой стрелки, отставание по фазе – по часовой стрелке.
Пример решения
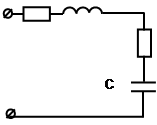
Дана цепь переменного тока с последовательным соединением элементов. Активное сопротивление катушки RК=4 Ом, индуктивность
L=38,2 мГн. Последовательно с катушкой включен резистор с активным сопротивлением R=2 Ом и конденсатор с емкостью 796,2 мкФ. К цепи приложено напряжение U=100 В.
Определить полное сопротивление цепи, силу тока, коэффициент мощности, активную, реактивную и полную мощности; напряжение на каждом сопротивлении. Начертить векторную диаграмму цепи.
 Краткая запись условия
Краткая запись условия
|
|
Дано: RК=4 Ом
|
L= 38,2 мГн
R=2 Ом
С=796,2 мкФ
U=100 В
Определить: z, I, cosj, P, Q, S, UR, UK, UL, UC.
Решение:
1. Переведем индуктивность и емкость в систему СИ. L=38,2∙10-3Гн, С=796,2∙10-6Ф.
2. Полное сопротивление цепи:
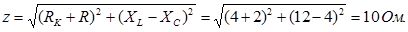
Для этого рассчитаем индуктивное сопротивление:
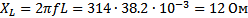
Емкостное сопротивление:
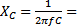 4 Ом
4 Ом
2.Сила тока в цепи: 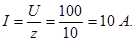
3.Коэффициент мощности: 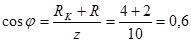
4.Активная мощность цепи:
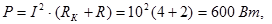 или
или
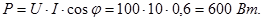
5.Реактивная мощность цепи:
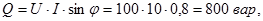 или
или
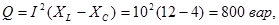 где
где
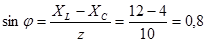
6.Полная мощность цепи:
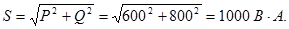
7.Напряжения на сопротивлениях цепи:
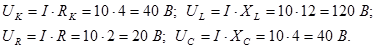
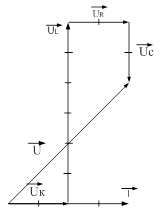
8. Построение векторной диаграммы:
а)Для построения векторной диаграммы задаемся масштабом по току mI =2,5 A /см и масштабом по напряжению mU =20 В/см.
б)Определим длины векторов тока и напряжения:
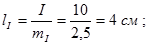
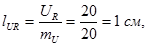
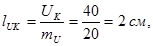
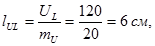
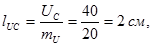
в) Построение начинаем с вектора тока I. Откладываем его по горизонтали длиной 4 см.
Вдоль вектора тока откладываем вектор напряжения на активном сопротивлении катушки UK
Из конца вектора UК откладываем в сторону опережения вектора тока на 90° вектор напряжения UL на индуктивном сопротивлении длиной 6 см.
Из конца вектора UL откладываем в сторону направления тока (горизонтально) вектор напряжения на резисторе UR, от конца этого вектора откладываем в сторону отставания от вектора тока на 90° (вниз) вектор напряжения на конденсаторе UC длиной 2 см.
Геометрическая сумма векторов UK, UR, UL и UC равна напряжению U , приложенному к цепи.
Задачи №№31-40
Цепь переменного тока содержит различные элементы (резисторы, индуктивности, емкости), включенные последовательно . Данные для своего варианта указаны в таблице.
Определите следующие величины,: полное сопротивление цепи z; ток I; активную Р, реактивную Q и полную S мощности, коэффициент мощности cosφ . Постройте в масштабе векторную диаграмму тока и напряжений.
| № | R1 , Ом | R2 , Ом | L , мГн | C , мкФ | U , В |
| 31 | 2 | 1 | 51 | 264 | 20 |
| 32 | 4 | 2 | 102 | 132 | 50 |
| 33 | 8 | 8 | 203 | 61 | 200 |
| 34 | 2 | 1 | 25.5 | 796,2 | 10 |
| 35 | 10 | 20 | 318.4 | 53 | 100 |
| 36 | 15 | 15 | 159,2 | 318,5 | 200 |
| 37 | 10 | 6 | 76,4 | 264,4 | 80 |
| 38 | 9 | 7 | 63,7 | 398 | 60 |
| 39 | 100 | 60 | 637 | 39,8 | 400 |
| 40 | 20 | 10 | 382 | 39,8 | 200 |

МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ ЗАДАЧ №№41-50
Задачи №№21-30 посвящены расчету разветвленных цепей переменного тока.
Пример
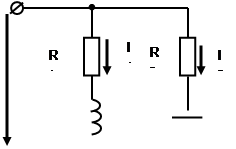
Катушка с активным сопротивлением R1=8 Ом, и индуктивным XL1=6 Ом соединена параллельно с конденсатором, емкостное сопротивление которого равно XC2=20 Ом.
К цепи приложено напряжение U=60 В.
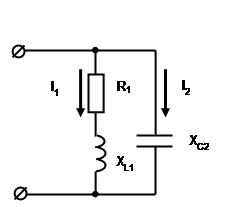 Определить: токи в ветвях и неразветвленной части цепи, активные и реактивные мощности ветвей и всей цепи, полную мощность цепи, углы сдвига фаз между током и напряжением в каждой ветви и во всей цепи.
Определить: токи в ветвях и неразветвленной части цепи, активные и реактивные мощности ветвей и всей цепи, полную мощность цепи, углы сдвига фаз между током и напряжением в каждой ветви и во всей цепи.
Построить векторную диаграмму токов и напряжения.
Краткая запись условия
Дано: R1=8 Ом
XL1=6 Ом
XC2=20 Ом
U=60 В
Определить : I1, I2, I, P1, P2, P, Q1, Q2, Q, S, j1, j2, j.
Решение :
1. Построим схему цепи (см.рис.).
2.Определим полное сопротивление каждой ветви:
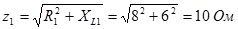 ,
,
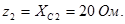
3.По закону Ома вычислим силу тока в каждой ветви:
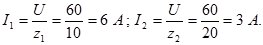
4.Определим углы сдвига фаз в ветвях:
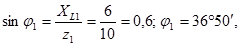
т.е. напряжение опережает ток, т.к. j1> 0;
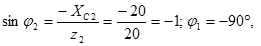
т.е. напряжение отстает от тока, т.к. j2< 0. По таблицам Брадиса находим: 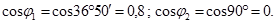
5.Найдем активные и реактивные составляющие токов ветвей: 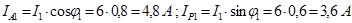
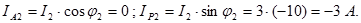
6.Сила тока в неразветвленной части цепи:
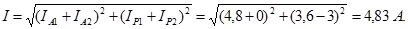
7.Коэффициент мощности всей цепи:
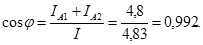
8.Мощности каждой ветви (активная, реактивная и полная):
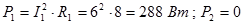 ,
,
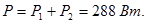
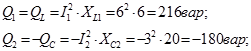
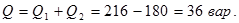
Реактивная мощность ветви с емкостью Q2 – отрицательная, т.к. угол j2< 0.
Полная мощность цепи: 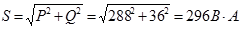
Проверка:
ток в неразветвленной части цепи можно определить и без разложения токов ветвей на составляющие
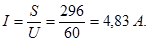
9.Построение векторной диаграммы:
а)Для построения векторной диаграммы задаемся масштабом по току mI =1 A/см и масштабом по напряжению mU=10 В/см.
б)Определим длины векторов тока и напряжения:
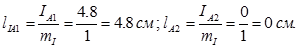 ,
, 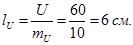
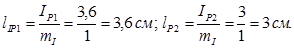
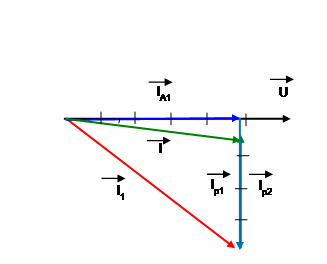 в) Построение начинаем с вектора напряжения U. Откладываем его по горизонтали длиной 6 см. Затем откладываем в масштабе вектор тока IА1, совпадающий по фазе с напряжением. Далее под углом 900 к вектору напряжения (в сторону отставания) откладываем вектор тока IР1. Геометрическая сумма этих токов равна току перв01ой ветви I1. Затем от конца вектора тока I1 откладываем под углом 900 от горизонтали в сторону опережения вектор тока IР2= I2. Геометрическая сумма токов в ветвях даст ток в неразветвленной части цепи I.
в) Построение начинаем с вектора напряжения U. Откладываем его по горизонтали длиной 6 см. Затем откладываем в масштабе вектор тока IА1, совпадающий по фазе с напряжением. Далее под углом 900 к вектору напряжения (в сторону отставания) откладываем вектор тока IР1. Геометрическая сумма этих токов равна току перв01ой ветви I1. Затем от конца вектора тока I1 откладываем под углом 900 от горизонтали в сторону опережения вектор тока IР2= I2. Геометрическая сумма токов в ветвях даст ток в неразветвленной части цепи I.
Ответ : I1=6 A, I2=3 A, I=4,83 A, P1=288 Вт, P2=0, P, Q1=216 вар, Q2=-180 вар, Q=36 вар,
S=296 ВА,
Задачи №№41-50
Конденсатор емкостью С соединен параллельно с катушкой L. Цепь подключена к источнику напряжением U, частотой f=50 Гц.
Начертить схему цепи. Определить в каждой ветви: полное сопротивление, силу тока. Определить силу тока в неразветвленной части цепи, активную, реактивную, полную мощность всей цепи.
Построить векторную диаграмму напряжения и токов
Таблица
| Обозначения величин | задачи | |||||||||
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | |
| U , B | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 |
| R 1 , Ом | 3 | 4 | 8 | 6 | 6 | 8 | 12 | 16 | 12 | 6 |
| Х L1 , Ом | 4 | 3 | 6 | 8 | 8 | 6 | 16 | 12 | 16 | 8 |
| R 2 , Ом | 8 | 6 | 3 | 8 | 16 | 12 | 10 | 6 | 8 | 8 |
| Х C2 , Ом | 6 | 8 | 4 | 6 | 12 | 16 | 3 | 8 | 6 | 20 |
|

|
|

 |








