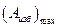Определение момента инерции маховика при постоянном приведенном моменте инерции механизма
При постоянном приведенном моменте инерции уравнение дви жения машины имеет вид
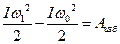
Или
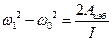
Т.е. разность между конечной и начальной угловыми скоростями будет тем больше, чем больше 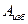 . Очевидно, что максимальная разность
. Очевидно, что максимальная разность 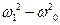 будет соответствовать максимальной избыточной
будет соответствовать максимальной избыточной 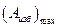 . Очевидно также, что максимальная разность
. Очевидно также, что максимальная разность 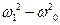 будет тогда, когда
будет тогда, когда 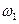 примет максимальное значение, а
примет максимальное значение, а 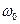 -минимальное значение. Тогда
-минимальное значение. Тогда
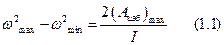
Выразим 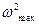 и
и 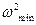 через среднюю угловую скорость
через среднюю угловую скорость 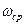 и коэффициент неравномерности хода
и коэффициент неравномерности хода 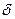 . Ранее мы имели (1.22 и 1.22а):
. Ранее мы имели (1.22 и 1.22а):
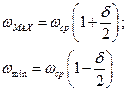
Возведем уравнение в квадрат, тогда
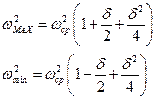
Членом 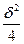 ввиду малости
ввиду малости 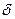 можно пренебречь, тогда
можно пренебречь, тогда
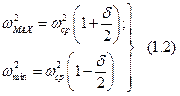
Подставляя эти значения в уравнение (1.1), получим
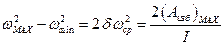
Решая это уравнение относительна I, получим
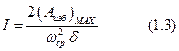
Таким образом, чтобы мащина йэигалась с заданным коэффициентом неравномерности 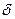 при заданной средней угловой скорости
при заданной средней угловой скорости 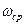 ее момент инерции должен определяться по уравнению (1.3).
ее момент инерции должен определяться по уравнению (1.3).
Момент инерции машины складывается из собственного момента инерции механизма 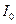 и момейта инерции маховика
и момейта инерции маховика 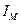 :
:
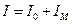
Откуда
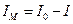
или окончательно момент инерции маховика равен
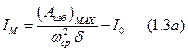
Величину 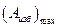 легко определить, если заданы приведенные моменты движущих сил
легко определить, если заданы приведенные моменты движущих сил 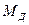 и сил сопротивления
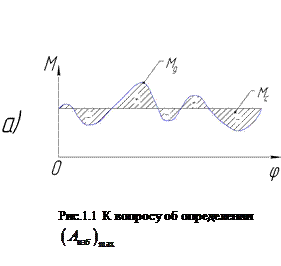
и сил сопротивления 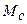 . Пусть эти моментй для периода установившегося движения заданы графиками, представленными на рис.1.1а. Избыточная работа
. Пусть эти моментй для периода установившегося движения заданы графиками, представленными на рис.1.1а. Избыточная работа 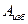 для различных участков определяется площадями, заключенными между
для различных участков определяется площадями, заключенными между 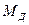 кривыми
кривыми 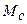 и , так как
и , так как
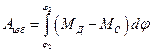
Однако нам нужно определить 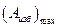 на участке, где угловая скорость изменяется от
на участке, где угловая скорость изменяется от 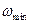 до
до 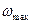 . По взаимному расположению графиков
. По взаимному расположению графиков 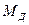 и
и 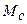 установить, при каком значении угла
установить, при каком значении угла 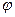 угловая скорость
угловая скорость 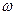 является максимальной и при каком — минимальной не всегда удается. И поэтому трудно определить
является максимальной и при каком — минимальной не всегда удается. И поэтому трудно определить