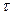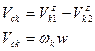Построение нормального зубчатого зацепления

Дата: 2025-06-02; Просмотры: 21
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

При построении нормального зубчатого зацепления должны быть известны: количества зубьев зубчатых колес z1 и z2, модуль т и угол зацепления α.

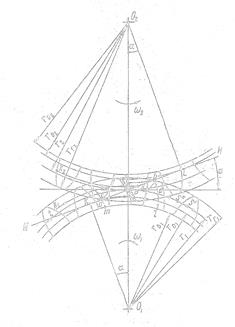
Построение зубчатого зацепления ведется в такой последователь­ности (рис. 5.16).

Вычисляем радиусы начальных окружностей r1 и r2 и межосевое расстояние А:

 

 

 

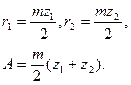
Проводим линию центров, отмечаем на ней центры О1 и О2 и полюс Р и наносим началь­ные окружности (окружности. на рисунке нанесены непол­ностью).

 

Через полюс Р проводим общую касательную к началь­ным окружностям (перпенди­кулярно к линии центров) и к ней под углом α - линию зацепления NN. Из центров О1 и О2 восстанавливаем перпендикуляры к линии зацепле­ния О1К и О2L. Длины этих перпендикуляров есть радиу­сы основных окружностей. Проводим эти окружности.

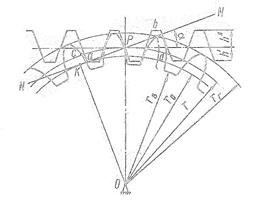
2. Вычисляем радиусы окружностей головок и впадин обоих колес и проводим эти окружности:

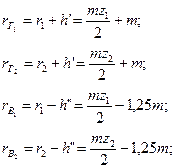
Рис. 5.16. Построение нормального зубчатого зацепления

Перекатывая линию зацепления сначала по одной основной окружности, а затем подругой, описываем точкой Р линии зацеп­ления эвольвенты (профили зубьев) в пределах от основной окруж­ности (или окружности впадин) До окружности головок (Построе­ние эвольвент на рисунке не показано. См. § 5. 4.)

 

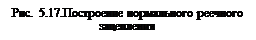В зависимости от количества зубьев радиус окружности впадин может быть больше радиуса основной окружности или мень­ше. В первом случае (rB > rO ) весь профиль зуба в пределах между окружностями головок и впадин очерчивается по эвольвенте. Во втором случае (rB < rO) профиль зуба очерчивается по эвольвенте только в пределах между окруж­ностями головок и основной (так как внутри основной окружности эвольвента расположена быть не может). В пределах между основ­ной окружностью и окружностью впадин профиль очерчивается отрезком радиальной прямой, сопрягаемой с эвольвентой. Построенные профили зубьев сопрягаются с окружностью впадин дугами радиусом ρ=0,3m..

Вычисляем толщину зуба и ширину впадины

 

 

 

 

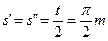
и откладываем по начальным окружностям в обе стороны от точки P по нескольку равных им дуг. Через полученные точки проводим, чередуясь, симметричные и подобные построенным ранее боковые профили зубьев. Для этого по первоначально построенным профи­лям можно из плотной бумаги вырезать шаблоны.

На этом построение зубчатого зацепления закончено.

 

Аналогично строится картина реечного зацепления (риc. 5.17).

Разница заключается лишь в том, что у рейки вместо окружностей

будут прямые линии. Профиль зуба рейки также очерчивается от­резком прямой, перпендикулярной линии зацепления (эвольвента основной окружности с бесконечно большим радиусом преобразует­ся в прямую).

 

 

2. Качественные показатели зацепления

Коэффициент удельного скольжения - учитывает степень влияния кинетических и геометрических факторов на износ зубьев.

Коэффициент перекрытия или плавности ε – учитывает плавность и непрерывность зацепления.

Коэффициент формы зуба Y – оценивает изгибную прочность зуба.

Коэффициент удельного давления Ө - учитывает влияние геометрии зуба на величину.

а) Коэффициент удельного скольжения.

 

 

 

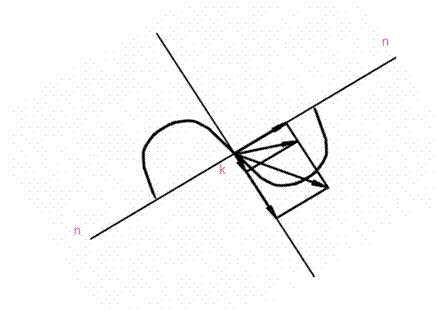
Чем дальше от полюса, тем выше скорость скольжения 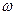значит ножка зуба изнашивается больше чем головка

 

;

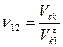
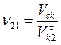
Зуб шестерней изнашивается больше чем зуб колеса.

 

 

б) Линия зацепления. Дуга зацепления. Коэффициент

перекрытия

 

Совершенно очевидно, что каждый зуб зубчатого колеса нахо­дится в зацеплении не на всем своем пути, а только на каком-то участке, т. е. в какой-то точке он входит в зацепление, а в какой-то - выходит из него.

Рассмотрим, как найти эти точки.

Допустим, колесо 1 - ведущее и вращается по часовой стрелке,

а колесо 2 - ведомое и вращается против часовой стрелки (рис. 5.18).

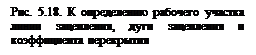В положении, изображенном на рис. 5.18, а, зубья этих колес еще не находятся в зацеплении, но при повороте колеса 1 в какой-то мо­мент правый профиль зуба еf вступит в соприкосновение (зацепление) с правым профилем зу­ба 2-gh. Где это произойдет? Совершенно очевидно, что первой вступит в зацепление точка g зуба 2 ведомого колеса, лежащая на окружности головок (какая точка зуба 1 первой вступит в зацепление, нам пока не видно). Но нам известно, что зубья мо­гут касаться только на линии за­цепления NN. Следовательно, первой точкой касания '(зацепле­ния) зубьев будет та, где точка g попадет на линию зацепления, т. е. точка пересечения окружно­сти головок ведомого колеса с линией зацепления - точка а. На рис. 5.18, б показано поло­жение зубьев в начале зацеп­ления.

Далее профиль еf будет на­жимать на профиль gh и сколь­зить по нему до тех пор, пока они не выйдут из зацепления. При этом зацепление (касание)

профилей будет происходить все время только на линии зацепления. Последней будет находиться в зацеплении точка е ведущего зуба, лежащая на окружности головок. Поэтому последней точкой зацепления будет точка пересечения окружности головок ведущего колеса с линией зацепления - точка b. Положение зубьев в конце зацепления пока за но на рис. 5.18, в.

При дальнейшем повороте колес зубья уже не будут нах

одиться в зацеплении (рис. 5.18, г).

Таким образом, зубья будут касаться только на участке аb. Этот участок называется р а б о ч и м у ч а с т к о м л и н и и з а ц е п л е н и я.

Дуги c1 d1 и c2 d2 между положениями соответствующих профи­лей зубьев в начале и конце зацепления для каждого из колес (эти профили показаны пунктирными линиями) есть пути, проходимые зубьями за время зацепления одной пары зубьев, измеренные по на­чальным окружностям. Так как начальные окружности катятся одна по другой без скольжения, то эти дуги равны между собой. Эти дуги называются д у г а м и з а ц е п л е н и я.

Рабочий участок аb отмечен также на рис. 5.16 и 5.17. Через точки а и b проведены (пунктирными линиями) положения правых профилей зубьев колеса 1 в начале и конце зацепления. Дуга cd на этом рисунке также является дугой зацепления колеса 1 (для коле­са 2 дуга зацепления не обозначена).

При работе зубчатых колес необходимо, чтобы в любой момент времени зубья находились в зацеплении. Для этого требуется, что­бы дуга зацепления была больше шага. В самом деле, каждый после­дующий зуб вступает в зацепление (в точке а), когда зуб пройдет по начальной окружности путь, равный шагу t. Поэтому путь, прохо­димый зубом за время зацепления одной пары зубьев (дуга зацеп­ления), должен быть больше шага. В противном случае первая пара зубьев выйдет из зацепления раньше, чем войдет в зацепление сле­дующая пара зубьев, т. е. будут такие промежутки времени, когда ни одна пaрa зубьев не будет находиться в зацеплении. Этого, ко­нечно, допускать нельзя.

Отношение дуги зацепления к шагу называется к о э ф ф и ц и ­е н т о м п е р е к р ы т и я :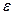

 

 

 

 

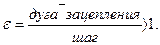
Это отношение должно быть больше единицы. На практике берется .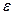

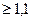Коэффициент перекрытия характеризует плавность зацепления 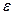, он показывает среднее количество пар зубьев, находящихся одно­временно в зацеплении. Чем больше коэффициент перекрытия, тем плавнее, спокойнее работает зубчатая передача. I

Рабочий участок линии зацепления аЬ равен дуге тl (рис. 5. 16), проходимой зубом за время зацепления по основной окружности. А так как дуги , проходимые зубом по различным окружностям, пропорциональны их радиусам, то

 

 

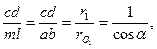
откуда

 

 

 

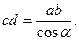
Подставляя это значение в формулу для определения коэффициента перекрытия, получим

 

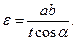(5.20)

 

Этой формулой удобно пользоваться при определении коэффи­циента перекрытия. При этом надо иметь в виду, что с изменением угла зацепления изменяется (при прочих равных условиях) и длина рабочего участка линии зацепления.