Графическое дифференцирование
Известно, что скорость является производной пути по времени
.
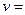
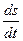Поэтому. если задана диаграмма пути s = f(t), то методом графического дифференцирования можно определить cкорость в любом положении.
На рис. 2.23 представлена диаграмма пути s = f (t). Определим скорость v в положении 1:
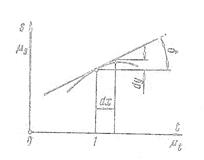
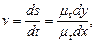
где dy.- элементарный отрезок (мм), изображающий в масштабе μs элементарное перемещение ds;
dx - элементарный отрезок (мм). изображающий в масштабе μt элементарное время dt
Отношение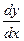 
, как это известно из математики, есть тангенс угла наклона касательной к оси абсцисс. Обозначив этот угол через 
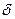, получим
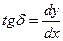
Тогда
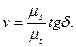
Таким образом, скорость в рассматриваемый момент времени пропорциональна тангенсу угла между касательной к кривой s - f(t) в соответствующей точке и осью t.
Формула 2.19 является основной формулой при графическом дифференцировании.
Имеется несколько методов графического дифференцирования. Рассмотрим два из них: метол касательных и метод хорд.
Метод хорд
Метод хорд заключается в следующем. Разбиваем кривую на ряд участков (участки могут быть неравными) и заменяем на этих участках кривые хордами (рис. 2. 25,а), т. е. неравномерное движение на каждом участке приближенно заменяем движением равномерным с постоянной скоростью, равной действительной средней скорости
на данном участке.
На оси t будущей диаграммы v = f(t) влево от начала координат на произвольном расстоянии Н выбираем точку О' (рис. 2.25,6). Из этой точки проводим лучи О'-1", О'-2",О'-3" и т. д., параллельные соответствующим хордам О-1', 1' -2', 2'-3' и т. д. Эти лучи отсекают на оси v отрезки О-1”, О-2', О-3" и т. д., пропорциональные средним скоростям на соответствующих участках. Откладывая равные этим отрезкам ординаты zi на соответствующих участках, получим ступенчатую линию 1"1"'2"'2"'3"'3'" и т. д. графика скорости. Истинный график скорости легко получить, проведя плавную кривую через уступы ступенчатого графика таким образом, чтобы площади заштрихованных площадок, расположенных с обеих сторон кривой на каждом участке, были одинаковы.
.
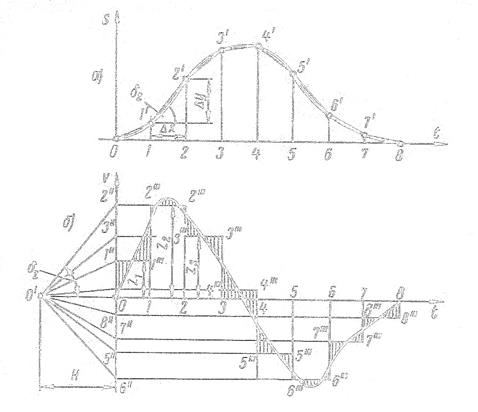
Рис. 2.25. Графическое дифференцирование по методу хорд.
При проведений кривой v = f(t) с достаточной для практики точностью можно принять, что она проходит через середины уступов 1"-1"', 2"'-2''', 3'''-3'" и т. д. Это облегчает построение кривой. Следует отметить, что при проведении хорд на графике s = f(t) нужно, чтобы эти хорды были достаточно близки к кривой. Если этого не получается, то участок следует разбить на более мелкие части. Например, на участке 1-2 (рис. 2.26) хорда аb далека от кривой, поэтому участок нужно разбить на два меньших участка (1-1' и, 1'-2) и на
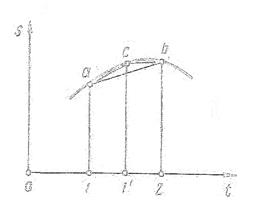них к кривой провести две новые хорды ac и cb
Определим масштаб скорости
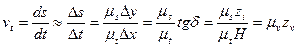
откуда масштаб равен
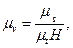
т. е. он определяется точно по такой же формуле, как и при дифференцировании по методу касательных.