Лекция 8. Корреляционный и регрессионный методы в эпидемиологии
Вопросы:
1. Парный коэффициент корреляции.
2. Регрессионный анализ
3. Коэффициент корреляции рангов Спирмена
1. Парный коэффициент корреляции эпидемиологии
Для практической работы эпидемиологов, связанной с выявлением факторов риска, наибольшее значение имеет корреляционный анализ. Необходимо подчеркнуть, что измерение связи допустимо лишь в случае, если ее наличие предполагается хотя бы теоретически. Параллельное изменение сопоставляемых показателей еще не свидетельствует об их взаимозависимости, так как оно может быть обусловлено случайным совпадением. Парный коэффициент корреляции рассчитывается следующим образом:
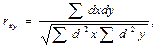
где rxy - коэффициент корреляции, x и y - коррелируемые ряды, dx и dy - отклонение каждого из чисел этих рядов от их средних, n - число парных членов в коррелируемых рядах.
Достоверность коэффициента корреляции определяется сравнением его с величиной вычисляемой средней ошибки. Средняя ошибка mr коэффициента корреляции равна:
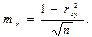
Коэффициент корреляции считается достоверным, если не менее чем в 3 раза превышает свою среднюю ошибку.
Данные о заболеваемости ОРВИ в Партизанском районе г.Минска в первой половине 2006г. и данные о содержании СО2 в воздухе района.
| Месяц | Число больных (x) | Удельный вес нестандартных выбросов (y) |
| 1 2 3 4 5 6 | 200 100 100 50 190 200 | 6 2 2 0 6 8 |
| Ср.значение | Мx =140 | Мy =4 |
1. Рассчитываем отклонение значений каждого члена ряда от среднего значения.
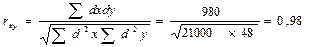
2. Достоверность коэффициента корреляции определяется сравнением его с величиной вычисляемой средней ошибки. Средняя ошибка коэффициента корреляции равна:
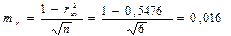 ,
, 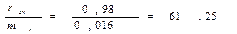 .
.
Более точно достоверность коэффициента корреляции определяется по специальной таблице (1) Приложение, табл.5. Для n=6 критическое значение r=0,917 для р<0,01. Следовательно, результаты корреляционного анализа указывают, что увеличение случаев заболевания детей в значительной степени зависит от загрязненности воздуха.
2Регрессионный анализ в эпидемиологии
Однако, часто заболеваемость зависит от многих других варьирующих признаков. Получить представление о том, насколько в среднем может измениться один из признаков при изменении другого, связанного с ним признака, можно путем вычисления коэффициента регрессии:
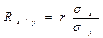 и
и 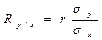
где R - коэффициент регрессии, r - коэффициент корреляции, sx и sy среднеквадратические отклонения для рядов х и y соответственно.
Рассмотрим насколько в среднем увеличивается число больных ОРВИ при увеличении на 1% нестандартных проб воздуха.
Из промежуточных этапов вычисления коэффициента корреляции легко получить соответствующие значения средних квадратических отклонений:
sх = 21000/5 = 4200 = 64,8; sy = 48/5 » 3,1, с увеличением числа нестандартных проб на 1% число больных ОРВИ увеличивается в среднем на 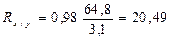 случая. Соответственно увеличение числа больных на 1 случай свидетельствует об увеличении числа нестандартных проб на
случая. Соответственно увеличение числа больных на 1 случай свидетельствует об увеличении числа нестандартных проб на 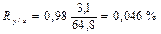 .
.
3. Коэффициент корреляции рангов Спирмена.
В случаях, если заболеваемость можно измерить лишь полуколичественно или ее значениям можно присвоить порядковые номера (ранги), то гипотезу о корреляционной связи проверяют, вычислив непараметрический коэффициент корреляции рангов Спирмена. Этот метод менее точен по сравнению с «классическим» вариантом нахождения коэффициента корреляции по количественным показателям. Однако из-за своей простоты метод ранговой корреляции находит широкое применение в эпидемиологической практике. Этому во многом способствуют массовость оцениваемых эпидемиологических явлений и значительные колебания исследуемых показателей.
1. В столбцы «ранги х» и «ранги y» заносим ранговые номера каждого из сравниваемых рядов в порядке возрастания или убывания. Если некоторые варианты повторяются, то их рангами будут среднеарифметические показатели из соответствующих порядковых номеров.
| Месяц | Число больных (х) | Удельный вес нестандартных выбросов (y) | Ранги x | Ранги y | D (x-y) |
| 1 2 3 4 5 6 | 200 100 100 50 190 200 | 6 2 2 0 6 8 | 5.5 2.5 2.5 1 4 5.5 | 4.5 2.5 2.5 1 4.5 6 | 1 0 0 0 -0.5 -0.5 |
2. Для каждой пары сопоставляемых значений определяется разность рангов и заносится в столбец d.
3. Расчитываем коэффициент корреляции рангов Спирмена по формуле
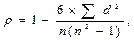
где r - коэффициент корреляции рангов, d – разность между порядковыми номерами рядов, n – число пар коррелируемых рядов.
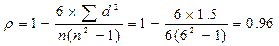
4. Определяем среднюю ошибку коэффициента корреляции для оценки его достоверности:
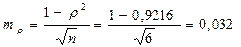 ,
, 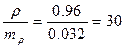
В связи с тем, что коэффициент корреляции более чем в 3 раза превышает свою ошибку, следует оценить его как достоверный. Достоверность рангового коэффициента также можно установить по специальным таблицам (1)приложение, табл.4. Оцениваем полученный коэффициент корреляции. При n=6 для уровня достоверности 95% критическое значение r=0,85. Следовательно, полученный коэффициент корреляции достоверен в высокой степенью точности.
Коэффициент корреляции рангов дает возможность оценить связь тогда, когда ее наличие обосновывается гипотезой о причинно-следственной зависимости заболеваемости с определенным фактором риска.
Литература:
1. Милютин А.А., Дудинская Р.А. Методы обработки информации, МИР им.А.Сахарова, 1999, 63 с.
2. Урбах В.Ю. Статистический анализ в биологических и медицинских исследованиях. –М.: Медицина,1975. –296 с.








