2. Категории экономической эффективности проектов реального инвестирования.
3. Затраты упущенных возможностей.
4. Продолжительность экономической жизни инвестиций. Фазы развития инвестиционного проекта.
5. Методы оценки экономической эффективности долгосрочных инвестиций. Определение чистой текущей стоимости (NPV); индекса рентабельности (PI).
6. Методы оценки экономической эффективности долгосрочных инвестиций. Определение внутренней нормы доходности (IRR); срока окупаемости (PP) инвестиционного проекта.
7. Методы оценка риска по инвестиционному проекту: анализ чувствительности, имитационное моделирование.
8. Методы оценка риска по инвестиционному проекту: методика изменения денежного потока, определение точки безубыточности проекта.
9. Анализ альтернативных проектов.
10. Формы и методы финансирования инвестиционных проектов: акционирование, банковский кредит, государственное финансирование.
11. Экономическая оценка инвестиций в акции (виды доходности, методы оценки риска вложений в акции).
12. Экономическая оценка инвестиций в облигации (виды доходности, оценка риска).
13. Инвестиционный портфель. Принципы формирования. Типы инвестиционного портфеля.
14. Доходность и риск портфеля, состоящего из нескольких финансовых активов.
15. Специфика нематериальных активов. Финансирование долгосрочных инвестиций в нематериальные активы.
16. Методы оценки инвестиционных вложений в нематериальные активы.
17. Цена капитала и ее роль в оценке инвестиционных проектов. Структура источников финансирования инвестиционных вложений.
18. Стоимость источников. Определение средневзвешенной цены инвестиционного капитала (WACC).
19. Анализ эффективности инвестиционных проектов в условиях инфляции.
20. Антикризисное управление и инвестиции
21. Неопределенность результатов инвестиционного проекта и риск принятия инвестиционного решения.
22. Инвестиционные качества ценных бумаг.
23. Оценка эффективности инвестиций в ценные бумаги.
24. Инвестиционные ресурсы предприятия, компании, фирмы.
25. Методы финансирования инвестиционных проектов.
26. Бюджетное финансирование.
27. Акционирование как метод инвестирования.
28. Лизинг как метод финансирования капитальных вложений.
29. Венчурное (рисковое) финансирование.
30. Сущность и особенности ипотечного кредитования.
Варианты практических заданий:
Тема 1. Простые процентные ставки
Пример: 16 января 2007 г. Банк выдал ссуду в 40 тыс.дол. до 14 ноября 2077 г. Включительно под 8,5% годовых. Определите:
1. размер процентных денег с использованием обыкновенного процента (Дгод = 360дней) с точным числом дней ссуды;
2. размер процентных денег с использованием точного процента (Дгод = 365 дней) с точным числом дней ссуды;
3. величину процентных денег с использованием обыкновенного процента с приближенным числом дней ссуды (в каждом месяце 30 дней)
Решение
Точное число дней пользования ссудой составит 302 дня.
1. Обыкновенные проценты с точным числом дней ссуды будут равны 2,852 тыс. дол.:
I = 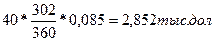
2. точные проценты с точным числом дней ссуды составят 2,813 тыс. дол.
I = 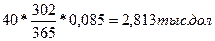
3. размер процентных денег в третьем варианте составил 2,814 тыс. дол.
I = 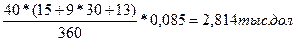
Следовательно, коммерческому банку в данном примере более выгодно использовать использовать первый метод начисления процентов. Записывается метод начисления процентов в этом случае 365/360. соответственно заемщику в данном случае более выгодно использование варианта расчета по точным числом дней пользования ссудой, т.е. метода начисления процентов 365/365. Предпочтительное использование точного или приближенного числа дней ссуды зависит от даты выдачи и возвращения денег. Отметим также, что дата выдачи кредита и дата его погашения считается за один день.
Задачи для самостоятельной работы
1. Какую сумму необходимо положить в банк на 138 дней под 9,25% годовых, чтобы получить 75 тыс. руб.?
2. За какое время депозит в размере 180 тыс. руб. при процентной ставке 15% годовых (простые проценты) принесет 18 тыс. руб. прибыли:
а) 180 дней;
б) 365 дней;
в) 391 день.
3. Депозит в 500 дол. Открыт на три года под 8% годовых (ставка простая процентная). В конце второго года банк увеличивает процентную ставку для сберегательных счетов до 5%. Какая сумма будет получена клиентом через 3 года:
а) если ставка по депозиту фиксированная;
б) если ставка по депозиту меняющаяся?
4. Рассчитайте величину процентов по кредиту размером 60 тыс. руб. сроком на полгода, если процентная ставка составляет 19% и
1) проценты простые;
2) проценты начисляются ежеквартально.
5. процентные ставки по срочным вкладам физических лиц ЗАО ММБ в конце 2007 г. Представлены в таблице.
| Валюта вклада | Сумма вклада | Срок вклада, дней | ||||
| 31-90 | 91-180 | 181-367 | 368-734 | 735-1 101 | ||
| Рубли | 25 000-250 000 | 3,00% | 4,25% | 6,00% | 7,50% | 7,50% |
| 250 000-750 000 | 3,40 % | 4,65% | 6,40% | 7,90% | 7,90% | |
| 750 000 – 1 500 000 | 3,60% | 4,85% | 6,60% | 8,10% | 8,10% | |
| 1 500 000 – 3 000 000 | 3,80% | 5,05% | 6,80% | 8,30% | 8,30% | |
| Евро | 1 000 – 10 000 | 2,00% | 2,25% | 2,50% | 3,00% | 3,505 |
| 10 000- 25 000 | 2,20% | 2,45% | 2,70% | 3,20% | 3,70% | |
| 25 000 – 50 000 | 2,30% | 2,55% | 2,80% | 3,30% | 3,80% | |
| 50 000 – 100 000 | 2,40% | 2,65% | 2,90% | 3,40% | 3,90% | |
1) Сделайте выводы о процентной политике банка по срочным вкладам.
2) Определите процентный доход клиента банка по вкладам:
а) вклад в сумме 400 тыс. руб. открыт на 367 дней;
б) вклад в сумме 18 тыс. евро открыт на полгода.
6. В момент открытия депозита была внесена сумма 1250 евро. Через полгода на счете было 1280 евро. Чему равен коэффициент дисконтирования и величина процентной ставки7
7. Фирма планирует получение кредита на сумму 2 млн. руб. На какой срок фирма можно взять кредит с тем, чтобы подлежащая возврату сумма не превысила 2,1 млн. руб.? банк использует простую процентную ставку – 20% годовых.
8. Предприятию 14 февраля была предоставлена ссуда в размере 200 тыс. руб. с погашением 14 июля того же года под процентную ставку 18 % годовых (проценты простые, год невисокосный). Рассчитайте сумму, причитающуюся к погашению, тремя методами (точные проценты с точным числом дней ссуды, обыкновенные проценты с точным числом дней ссуды, обыкновенные проценты с приближенным числом дней ссуды).
9. Клиент открыл депозит в размере 1500 евро сроком на два года по годовой процентной ставке 6%. В конце первого года банк поднимает процентную ставку по депозитам до 6,5%. Какая сумма будет на депозите через два года?
10. Фирма приобретает оборудование стоимостью 2,5 млн. руб. и обращается в банк с целью получения кредита на эту сумму сроком на восемь месяцев. Банк предлагает два варианта представления кредита:
1) номинальная процентная ставка 16%, погашение основной суммы долга и процентов по нему в конце срока, комиссионные составляют 1% от суммы кредита;
2) номинальная процентная ставка 15 %, проценты авансовые, а основная сумма долга погашается в конце срока.
Сравните реальную доходность банка по двум предположенным вариантам. Какой вариант выгоднее заемщику и почему?
11. Через 120 дней с момента подписания кредитного договора заемщик должен вернуть 750 тыс. руб. Процентная ставка по кредиту составляет 18 %. Чему равна первоначальная сумма долга?
12. Кредит в сумме 1,5 млн.дол. предоставлен клиенту на срок полгода по ставке 16%. Компенсационный остаток на счете составлял на весь срок кредита 10%. Какую сумму должен иметь в наличии клиент для возврата кредита банку? Чему равна наращенная сумма?
13. определите срок кредита в днях, если заемщик должен вернуть банку 900 тыс.руб., процентная ставка равна 18% а сумма кредита составляла 869 тыс.руб.
14. Под какую процентную ставку был выдан кредит размером 800 тыс.руб. на срок 200 дней, если наращенная сумма составила 865,75 тыс.руб.?
15. Чему равен коэффициент наращения и сумма процентов, если кредит был выдан на срок три месяца в размере 130 тыс.руб., а заемщик обязан вернуть 152 тыс.руб.?
Тема 2. Сложные проценты и расчеты с использованием учетных ставок. Определение процентной ставки в условиях инфляции
Пример. 1) Кредит в размере 400 тыс. дол. выдан на 2,5 года, процентная ставка равна 5,4%. Определите наращенную сумму (или сумму долга на конец срока).
Решение
В этом примере срок пользования ссудой состоит из целой и дробной частей. Определить наращенную сумму можно двумя способами:
1) воспользоваться формулой сложных процентов, и тогда наращенная сумма будет равна:
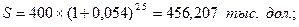
2) воспользоваться смешанным методом, когда за целое число лет начисляются сложные проценты, за дробную часть периода – простые проценты. Тогда в нашем примере:
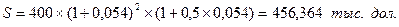
Результаты расчетов показывают, что при смешанном методе (второй способ) размер процентного дохода банка (или издержки заемщика) больше, чем при использовании формулы сложных процентов.
2) В конце пятого года по векселю должны быть получены 1,5 тыс. дол. Владелец векселя учитывает его в банке в конце второго года и получает 1140 дол. Каков размер учетной ставки, взимаемый банком?
Решение
Поскольку размер дисконта (S-P) равен 360 дол. (1500-1140), а до погашения векселя осталось 3 года, величина учетной ставки будет равна 8%:
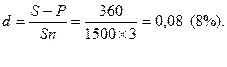
Задачи для самостоятельной работы
1) Кредит на сумму 50 тыс. евро выдан на два года. Какую сумму должен вернуть заемщик, если процентная ставка по кредиту была установлена в размере 13%?
2) Депозит в размере 900 тыс. руб. был открыт на три года. По окончании срока депозита клиент получил 932,4 тыс. руб. Чему равна сложная процентная ставка по депозиту?
3) Определите сумму кредита, выданного банком под 20% годовых, если через два года заемщик выплатил 3 млн 146 тыс. руб. Чему равен процентный доход банка?
4) Депозит размером 500 тыс. руб. открыт на два года. Какая сумма будет возвращена клиенту, если по сложной процентной ставке по депозиту начислялось 10%? Какова будет реальная покупательная способность денег, полученных клиентом, если уровень инфляции составил в первый год 11,5 %; во второй год 9,5%?
5) Сравните суммы процентов по кредиту в 1 млн руб. на срок четыре месяца в двух банках, если известно, что в первом банке проценты начисляются ежемесячно, а во втором – идет непрерывное начисление процентов. Номинальная процентная ставка по кредиту одинакова в двух банках и составляет 18 %.
6) Сберегательный сертификат куплен за 100 тыс. руб., выкупленная его сумма – 160 тыс. руб., срок – 2,5 года. Уровень доходности инвестиций в виде годовой ставки сложных процентов равен:
а) 20,68%;
б) 21,00%;
в) 21,50%?
7) Депозит в размере 350 тыс. руб. открыт на два года. Начисление сложных процентов осуществляется по процентной ставке в следующем размере: в первый год – 8%; во второй год – 8,5%. Определите сумму на депозите через два года и размер процентов, полученных вкладчиком.
8) Ссуда в размере 400 тыс. руб. выдана полгода. Сравните результаты наращения при номинальной ставке 18%, если проценты начисляются:
а) по простой процентной ставке;
б) по сложной процентной ставке.
9) Сумма вклада составила 200 тыс. руб. Определите срок, в течение которого проценты по вкладу составляют 46 420 руб., если банк начисляет сложные проценты в размере 11% годовых.
10) Определите сложную процентную ставку по кредиту размером 12 млн руб. на срок два года, если заемщик при единовременном погашении основного долга и процентов по нему выплатил банку 1 млн 699 тыс. руб.
11) Чему равна сумма процентов, по депозиту, открытому на сумму 600 тыс. руб. на срок два года и по номинальной сложной процентной ставке 9% годовых?
12) На какую сумму следует открыть депозит, чтобы через полтора года на счете вкладчика было 400 тыс. руб., если банк предлагает по депозитам на этот срок сложную процентную ставку 10 % годовых?
13) Реальная доходность банка по рублевому кредиту на срок два года, если годовая процентная ставка составляет 16%, годовой уровень инфляции – 9,5 %, составит:
а) по этим данным рассчитать нельзя;
б) 6,50%;
в) 5,94%.
14) В конце пятого месяца по векселю должны быть получены 1,5 тыс. дол. владелец векселя учитывает его в банке в конце второго месяца и получает 1320 дол. Размер учетной ставки равен:
а) 16,0%;
б) 2,67%;
в) 10,67%.
15) Лицо, управляющее портфелем ценных бумаг, получает на протяжении пяти лет в среднем по 16% в год. Известно, что в первые два года средний годовой доход составлял 12%. Чему равен средний годовой доход в оставшиеся три года?
Тема 3. Эквивалентность процентных ставок и консолидация платежей
1) Какая эффективная ставка соответствует номинальной ставке в 12% при начислении процентов два раза в месяц?
Решение
В этом примере i=0.12; m=2 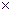 12=24.
12=24.
Используя формулу для расчета эффективной процентной ставки, получим iэф= 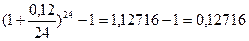 , т.е. эффективная процентная ставка составила 12,716%.
, т.е. эффективная процентная ставка составила 12,716%.
2) Определите непрерывную процентную ставку, эквивалентную номинальной ставке i=6% с ежеквартальным начислением процентов.
Решение
При i=0.06 и m=4 непрерывная ставка r будет равна 5,955%:
r= 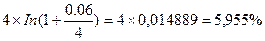
3) Банк принимает депозиты на три месяца по ставке 12%; на полгода – по ставке 13% и на год – по ставке 14%. Определите наилучший вариант вложения средств на год с учетом возможности переоформления трехмесячных и шестимесячных депозитов с начисленными процентами.
Решение
Рассчитаем эффективную годовую ставку при переоформлении депозитов:
а) при переоформлении трехмесячных депозитов эффективная ставка будет равна iэф= 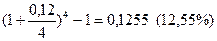 ;
;
б) при переоформлении шестимесячных депозитов
iэф= 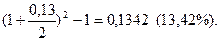
Следовательно, банк разрабатывает процентную политику так, чтобы стимулировать вложение средств на год по ставке 14%, поскольку эффективные ставки в вариантах а) и б) оказались ниже.
4) В марте 2007 г. фирма получила кредит в двух банках: в банке А кредит на сумму 100 тыс. дол. должен быть погашен 15 апреля 2007 г., и в банке Б кредит на сумму 80 тыс. дол. должен быть погашен 20 мая 2008 г. В связи с чрезвычайными обстоятельствами фирма обратилась к банкам с просьбой о продлении срока выплат по кредитам соответственно до 1 декабря 2010 г. Процентная ставка банка А АО кредиту – 13,9%, в банке Б – 14,5%.
Определите суммы, подлежащие возврату банкам по новому соглашению.
Решение
В банке А фирма продлевает кредит на 230 дней (по Приложению 1 15 апреля соответствует порядковый номер 105, а 1 декабря – 335, откуда Д=35-105=230 дней). Расчет процентов ведется на основе точного числа дней в году Дr=365 дней.
Поскольку речь идет о краткосрочном соглашении, наращенная сума определится с использованием простой процентной ставки:
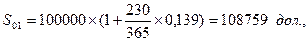
т.е. фирма должна будет возвратить первому банку 108759 дол.
В банке Б фирма продлевает кредит на два года и 104 дня (по Приложению 1 определяем порядковые номера для 1 сентября и 20 мая, тогда Д=244-140=104 дня).
В этом случае определение наращенной суммы банку целесообразно осуществить по смешанному методу:
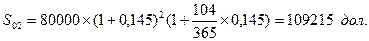
Банку Б фирма должна вернуть 1 сентября 2010 г. 109215 дол.
Задачи для самостоятельной работы
1) Стоимость нового автомобиля составляет 15 тыс. дол. Если процентная ставка в банке на вклады сроком более года равна 6%, на какую сумму следует открыть депозит, чтобы собрать в течение двух лет 15 тыс. дол.? Проценты по вкладу начисляются ежеквартально.
2) Клиенту требуется через полгода иметь на счете 10 млн руб. На какую процентную ставку рассчитывает вкладчик, если собирается положить в банк 9,8 млн руб. (проценты начисляются ежеквартально)?
3) На счет в размере 30 тыс. руб., открытый в банке «Кредитный Союз», проценты начисляются ежеквартально. Определите сумму на счете через полгода, если процентная ставка составляет 7%.
4) Туристическая путевка в Австралию стоит 2,5 тыс. дол. Клиент открывает депозит в банке на сумму 2200 дол. Сколько времени потребуется, чтобы накопить требуемую для поездки сумму, если процентная ставка в банке по депозитам на открытую сумму составляет 6%, а проценты начисляются ежеквартально?
5) Сколько лет требуется клиенту, чтобы накопить 7 тыс. дол. на депозите в банке, если на счете 3 тыс. дол., а годовая процентная ставка по депозиту – 9%? Проценты начисляются раз в полугодие.
6) Вексель номиналом 10 тыс. руб. учитывается банком с дисконтом 1875 руб., за три месяца до погашения. Какая простая процентная ставка соответствует примененной банком учетной ставке?
7) Определите эффективную ставку с тем, чтобы получить такую же наращенную сумму, как и при использовании номинальной ставки j=18%, при ежеквартальном начислении процентов:
а) 18,5%;
б)18,9%;
в)19,25%.
8) Вкладчик предпочтет следующий вариант вложений средств:
1) вклад, на который ежегодно начисляется 6%;
2) вклад, на который каждые полгода начисляется 5,9%;
3) вклад, на который начисляется 5,7%, с непрерывном начислением.
9) Рассчитайте величину процентов по кредиту размером 50 тыс. руб. сроком на полгода, если процентная ставка составляет 18% и
1) проценты простые;
2) проценты начисляются ежеквартально.
10) Банк начисляет на депозит размером от 500 тыс. руб. ежеквартально проценты по номинальной годовой ставке 10% годовых. Определите сумму процентов, начисленных на вклад размером 600 тыс. руб. за два года.
11) Эффективная годовая ставка при начислении банком процентов ежеквартально составляет 12,56%, а при начислении процентов ежемесячно ее величина равна 12,68%. Чему равна номинальная годовая ставка?
12) В рекламном объявлении финансовой компании указывается, что вложенная клиентом сумма ежедневно увеличивается на 0,26%. Определите эффективную годовую процентную ставку при заключении договора с компанией на три месяца (90 дней).
13) Предприятию необходим кредит в размере 500 тыс. дол. сроком на два года. Два банка предлагают следующие условия займа. В одном банке кредит предоставляется под 13% годовых (сложная процентная ставка). В другом банке – 12%, начисление процентов – по кварталам. Погашение долга и процентов осуществляется в конце срока кредита.
Определите, в каком банке выгоднее условия предоставления кредита для клиента и на сколько меньше финансовые издержки по обслуживанию долга.
14) Вклад на сумму 500 тыс. руб. помещен в банк на квартал ежемесячным начислением процентов по номинальной ставке 12% годовых. Каков будет реальный доход вкладчика при ожидаемом месячном уровне инфляции 2%?
15) Какие условия предоставления кредита более выгодны банку:
а) 15% годовых, начисляемых ежемесячно;
б) 16% годовых, начисляемых ежеквартально;
в) 17% годовых, начисляемых по полугодиям?
Тема 4. Анализ потоков платежей
Пример: Клиент в течение пяти лет в конце каждого квартала перечисляет в банк по 200 дол. Какая сумма будет на счете клиента в конце срока, если процентная ставка начисляется:
А) ежеквартально;
Б) по полугодиям?
Банк начисляет сложные проценты по ставке 6% годовых.
Решение
Параметры ренты: 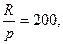 n=5, P=4, i=0.06; a) m=4; b) m=2
n=5, P=4, i=0.06; a) m=4; b) m=2
А) При начислении процентов ежеквартально получим следующее значение наращенной суммы:
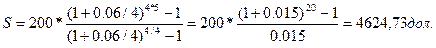
Таким образом, наращенная сумма при ежеквартальном начислении процентов составляет 4624,73 дол.
Б) При начислении процентов по полугодиям получим:
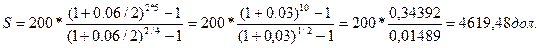
Следовательно, при изменении хотя бы одного из дополнительных условий финансовой ренты, изменяется размер наращенной суммы.
Задачи для самостоятельной работы
1. Новый автомобиль понравившейся вам марки стоит 10 тыс. дол. Две фирмы предлагают разные условия его приобретения:
1) первая фирма предлагает выплачивать 300 дол. В месяц в течение двух с половиной лет (30 месяцев) при условии оплаты наличными 10,0% от стоимости автомобиля;
2). Вторая фирма делает скидку с цены в размере 1 тыс.дол.
Какое предложение более выгодно покупателю:
А) первой фирмы;
Б) второй фирмы;
В) предложения равноценны.
Обоснуйте ваш вывод.
2. Ежемесячно клиент перечисляет на счет в банке по 200 дол. Какая сумма будет на счете через три месяца, если деньги поступают на счет:
А) в начале каждого месяца;
Б) в конце месяца?
Проценты начисляются ежемесячно, а процентная ставка банка по депозиту составляет 6%.
3. От сдачи в аренду здания предприятие получает в конце каждого квартала доход в размере 6 тыс.дол., которые переводит на депозит в банке. Какая сумма будет получена арендодателем в банке в конце года, если по депозиту раз в полгода банк начисляет 6% годовых?
4. В конце каждого полугодия учащийся должен вносить за обучение 2 тыс.дол. на протяжении пяти лет. Сколько ежемесячно (в начале месяца) следует вносить в банк, чтобы накопить 2 тыс. дол. К концу полугодия, если процентная ставка банка составляет 6 %, а проценты начисляются ежемесячно?
5. Молодая семья, получив в наследство дачный участок, сдает его за 800 дол. В месяц и перечисляет эту сумму на счет в банке «ВТБ 24» под 7,8% с ежемесячными начислениями процентов. С этого же счета семья ежемесячно перечисляет в Сбербанк платежи по кредиту, выданному на два года в размере 15 тыс.дол. за полгода до открытия счета в «ВТБ 24». Какая сумма будет на счете в «ВТБ 24» через год после открытия счета, если процентная ставка по кредиту, оформленная в Сбербанке, составляет 15%.
6. Менеджеры энергосистемы разрабатывают предложение для юридических лиц по графику платежей за потребляемую электроэнергию. По первому предложению оплата должна полностью поступать на 10-й день месяца. В соответствии со вторым предложением месячный платеж разбивается на три равные выплаты: 1-го числа месяца, 5-го числа и 10-го числа месяца. Какое предложение наиболее выгодно поставщику электроэнергии? Обоснуйте ваш вывод.
7. Клиент обратился в банк с просьбой о предоставлении кредита на покупку автомобиля, сроком на 1.5 года, уведомив банк, что ежемесячно может перечислять 1 тыс.дол. на какую сумму кредита может рассчитывать клиент, если процентная ставка, предложенная банком, составляет 9 %, а комиссия за ведение счета – 0,5% от суммы кредита? Определите издержки клиента по кредиту.
8. Фирма вносит в банк в начале каждого полугодия по 250 тыс.руб. в течение двух лет. Банк производит начисление процентов также дважды в год из расчета 12% годовых. Определите наращенную сумму по окончании ренты.
9. По инвестиционному проекту фирма предполагает получить прибыль в следующих размерах:
I квартал – 30 тыс. дол.;
II квартал – 32 тыс. дол.;
III квартал – 40 тыс.дол.;
IV квартал – 48 тыс.дол.
Предполагаемый срок окупаемости вложений – один год. Определите сумму инвестиций в начале года, приняв ставку дисконтирования 12 %.
10. Годовая рента – 10 тыс. евро, срок составляет два года, выплачивается с разными дополнительными условиями:
I вариант. Платежи производятся ежемесячно, проценты начисляются ежеквартально.
II квартал. Платежи в конце года, проценты начисляются ежеквартально.
III квартал. Платежи в конце года, начисление процентов в конце года.
Сравните приведенную стоимость по трем вариантам платежей.
11. на 1 июля 2006 г. На счете клиента банка имелось 1700 евро. По состоянию на 1 июля 2008 г. На счете должно быть 3500 евро. Какую сумму должен перечислять клиент ежеквартально (в конце каждого квартала), если процентная ставка по депозиту составляет 8%, а проценты начисляются по полугодиям.
12. В течение трех лет ежемесячно выплачивается (в конце месяца) 1200 евро. Какова приведенная стоимость аннуитета, если процентная ставка составляет 12%?
13. В течение полугода ежемесячно на счет в банке поступало по 8 тыс. руб. Еще через полгода счет был закрыт. Какую сумму получил клиент, если процентная ставка по вкладу составляла 9%, а проценты начислялись ежемесячно?
14. Предприятие берет в лизинг оборудование стоимостью 70 тыс. евро на пять лет. Ежегодные платежи по лизингу, выплачиваемые в начале каждого года, составляют 16300 евро. Какова доходность этой операции для лизинговой компании?
15. Какую сумму необходимо положить на депозит под 10% годовых, чтобы в течение трех лет можно было бы ежегодно изымать в конце года 5 тыс. руб.? Выплаты производятся как за счет накопленных процентов, так и за счет суммы, положенной на депозит (проценты начисляются по полугодиям).
Тема 5. Выбор варианта погашения долга и составление плана погашения кредита
Пример:
1. Банк предлагает фирме кредит, который будет выдаваться раз в два месяца на протяжении двух лет рентой постнумерандо, с начислением процентов ежемесячно в размере 12% годовых (сложная процентная ставка). Возврат кредита осуществляется единовременным платежом спустя год после последнего платежа банка. Чему будет равна сумма возврата кредита фирмой банку, если каждые два месяца фирма будет получать по 1 тыс. дол.?
Решение
Запишем исходные данные для определения наращенной суммы:
i = 0.12; n = 2; R/p = 1000 дол.; m = 12; p = 6; T = 1.
Сумма возврата кредита банку будет равна:
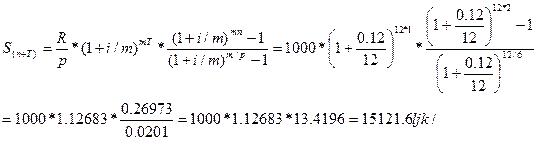
Задачи для самостоятельной работы
1. Получен кредит на покупку автомобиля («Автокредит») на сумму в размере 300 тыс. руб. на срок три года. так как приобретаемый автомобиль новый, то процентная ставка составляет 9%. Выплаты по кредиту происходят ежемесячно в начале месяца. Определите, сколько заемщик должен выплачивать банку ежемесячно, если проценты начислялись ежемесячно на остаточную сумму долга, а возможность долгосрочного погашения использована не была.
2. На основании приведенного плана погашения трехмесячного потребительского кредита определите сумму кредита и размер процентной ставки, проценты начисляются на остаточную сумму долга (руб.):
| Номер платежа | Сумма погасительного платежа | В том числе | |
| Проценты | Погашение основного долга | ||
| 1 – й | 6000 | 346 | 5654 |
| 2 – й | 6000 | 247 | 5753 |
| 3 - й | 6000 | 125 | 5875 |
3. Кредит в размере 3,5 млн. руб. выдан на пять лет под 20% годовых. По условиям контракта погашение основного долга должно производиться равными платежами в конце года с начислением процентов также в конце года. составьте план погашения кредита.
4. Кредит в размере 30 млн. руб. должен быть погашен в течение трех лет равными погасительными платежами в конце года. процентная ставка 1% годовых, ежегодное начисление процентов также в конце года. платежи, обеспечивающие погашение основного долга, должны увеличиваться в геометрической прогрессии на 5 % ежегодно. Составьте план погашения кредита.
5. Получен кредит в размере 1,5 млн. руб. на два года под 12 % годовых. Погашение основного долга и выплата процентов по нему ежеквартальные равными погасительными платежами в конце периода ренты. Определите величину невыплаченного основного долга на начало второго года погашения.
6. Кредит размером 2 млн. руб. выдан на четыре года под 16% годовых с начислением процентов в конце каждого квартала года на остаточную сумму долга. Составьте план погашения кредита с равными погасительными платежами в конце каждого квартала.
7. Кредит в размере 1 млн. дол., выданный на два года под 12% годовых, погашается равными ежеквартальными взносами начиная через год с даты подписания договора. Составить план погашения кредита, если проценты начисляются ежеквартально на остаточную сумму долга, а размер комиссионных за обязательство составляет 0,5% от суммы кредита.
8. Кредит в размере 0,5 млн. дол., выданный на год под 10 % годовых погашается ежеквартальными взносами с равномерным погашением основного долга начиная с даты подписания договора. Составьте план погашения кредита, если проценты начисляются на остаточную сумму долга, а размер комиссионных за обязательство составляет 1% от суммы кредита. Определите размер процентных выплат.
9. Кредит, предоставленный организации на пополнение остатка оборотных средств, составляет 600 тыс. руб. и выдан на полгода. Процентная ставка по кредиту составляет 18%. Рассматриваются два варианта погашения долга:
1) выплата процентов осуществляется в начале каждого месяца от остаточной суммы долга, а основная сумма погашается в конце каждого квартала равными платежами;
2) возврат кредита выполняется равными погасительными платежами в конце каждого месяца при ежемесячном начислении процентов.
Составьте план погашения кредита для каждого варианта и ответьте на вопрос, равнозначны ли для банка варианты погашения кредита с точки зрения доходов и кредитного риска?
10. Банк выдает кредит 30 тыс.дол. тремя равными суммами в начале каждого полугодия, процентная ставка по кредиту – 12%, проценты начисляются по полугодиям. Погашение кредита начисляется через полгода после последней выплаты банка. Составьте план погашения кредита, если используется ежеквартальное погашение общей суммы долга и процентов равными платежами в течение года на момент первого платежа.
11. Банк выдает 100 тыс. евро на два года под 12% годовых. Погашение долга производится ежеквартальными взносами начиная через полгода с даты подписания договора. Начисление процентов производится ежеквартально, погасительные платежи равны по величине. Комиссионные банка за обслуживание долга составляют 0,5%.
Разработайте план погашения долга и определите финансовые издержки клиента банка.
12. Кредит в сумме 150 тыс. руб., выданный на три года под 18% годовых, подлежит погашению равными ежегодными выплатами в конце каждого года, проценты начисляются также в конце года. После выплаты второго платежа достигнута договоренность между кредитором и заемщиком о продлении срока погашения на два года, но с увеличением процентной ставки с момента конверсии до 20%.
Составьте план погашения оставшейся части долга.
13. Малое предприятие погашает кредит в размере 600 тыс. руб. равномерными выплатами основного долга через каждые три месяца на протяжении года. Проценты выплачиваются ежемесячно от остаточной суммы долга, процентная ставка составляет 16% годовых. Определите размер каждого погасительного платежа и сумму процентов по кредиту.
14. Отделение Сбербанка России предлагает образовательный кредит на оплату обучения в высшем учебном заведении (дневная форма) на следующих условиях:
1) кредит выдается на срок шесть лет;
2) процентная ставка по рублевому кредиту 20%;
3) банк выдает не более 70% от общей стоимости обучения.
Разработайте схему погашения кредита при стоимости обучения 390 тыс. руб. для следующих вариантов:
1) погашение осуществляется равными погасительными платежами ежеквартально (в начале квартала) при ежеквартальном начислении процентов;
2) за период обучения (пять лет) заемщик ежемесячно (в начале месяца) выплачивает только проценты, а основной долг погашается в течение шестого года равными долями ежеквартально (в конце каждого квартала). За этот год проценты начисляются ежемесячно от остаточной суммы долга.
15. Программа ипотечного кредитования одного из московских банков предусматривает предоставление кредита на приобретение квартиры на первичном рынке семьям, имеющим доход не ниже 1 тыс. дол. в месяц.
При приобретении квартиры стоимостью в 50 тыс. дол. заемщик оплачивает 25% от ее стоимости наличными. На остальную сумму банк предоставляет ипотечный кредит на три года под 12% годовых в валюте.
Погашение кредита производится ежемесячно равными погасительными платежами. Определите сумму разового погасительного платежа и проценты по ипотечному кредиту, если комиссия за выдачу кредита составляет 2% от суммы предоставленного кредита.
Составьте план погашения кредита.
Тема 6. Модели оценки облигаций
Пример:
1. Определите доходность к погашению облигации номиналом 1 тыс. дол. с 10%-ной купонной доходностью, до погашения которой осталось 1,5 года, если курс облигации составляет 98,5, а купонный доход выплачивается по полугодиям.
Решение
Текущая стоимость облигации, исходя из курса, составляет 985 дол. 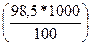 , а купонный доход за полугодие 50 дол.
, а купонный доход за полугодие 50 дол. 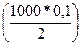 .
.
Следовательно, можно записать такое уравнение.
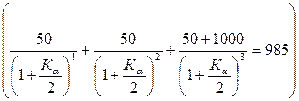
Решив уравнение, получим величину Кα=0,1106 т.е. доходность по облигации составляет 11,06%.
2. Облигация номиналом 1 тыс. руб., с купонной ставкой 9,3% и сроком обращения три года продана за два года до погашения. По какой цене ее будет приобретать инвестор, если рыночная процентная ставка по облигации составляет 10%, а купоны выплачиваются раз в год.
Решение
Современная стоимость облигации определится на основе дисконтирования будущих денежных потоков в течение двух лет до погашения облигации.
Через год после приобретения облигации инвестор получит купонный доход в размере 93 руб. (1000 х 0,093).
Еще через год он получит такой же купонный доход плюс номинал, т.е. через два года доход инвестора составит 1093 руб.
Современная стоимость облигации при ставке дисконтирования 10% составит 987,85 руб.:
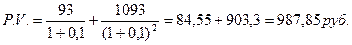
Таким образом, при рыночной доходности в 10% цена облигации за два года до погашения должна составить 987,85 руб. Если цена будет выше рассчитанной суммы, значит доходность к погашению будет меньше 10%. Если же цена будет меньше 987,85 руб., инвестору будет обеспечиваться доходность к погашению больше 10%.
3. Две облигации разных эмитентов имеют следующие параметры:
| № п/п | Параметр | Облигация Z | Облигация О |
| 1 | Срок обращения, лет | 3 | 5 |
| 2 | Номинальная стоимость, руб. | 1 000 | 1000 |
| 3 | Купонная ставка, % | 10,0 | 12,0 |
| 4 | Доходность к погашению, % | 9,5 | 14,0 |
| 5 | Выплаты купонов | в конце года | в конце года |
Какую из представленных облигаций можно рекомендовать приобрести инвестору и почему?
Решение
Для ответа на поставленный вопрос сравним дюрацию двух облигаций.
Первым шагом является расчет приведенной стоимости будущих потоков платежей по каждой облигации.
В конце каждого года по облигации Z будут выплачиваться купоны в размере 100 руб. (1000 х 0,1) и в конце третьего года кроме купонной выплаты будет погашен номинал облигации 1000 руб.
По облигации Q потоки платежей будут представлены в конце года купонными выплатами в размере 120 руб. (1000 х 0,12), а также в конце пятого года будет выплачен номинал облигации 1000 руб.
Выполним расчет современной стоимости облигаций.
1) Для облигации Z ставки дисконтирования составляет 9,5%:
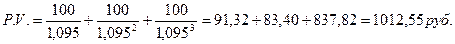
2) Для облигации Q ставка дисконтирования 14%, с учетом которой современная стоимость всех будущих потоков составляет:
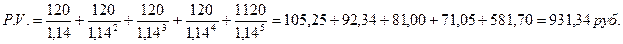
Расчет дюрации производится по средней арифметической взвешенной из интервалов времени от начала выпуска до каждого платежа, и в качестве веса используется доля каждого дисконтированного платежа в приведенной стоимости облигации.
1) Дюрация облигации Z:
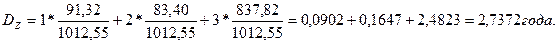
2) Дюрация облигации Q:
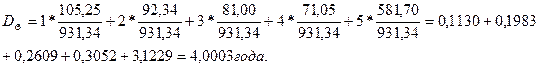
Поскольку дюрация облигации Z меньше, чем дюрация облигации Q риск для инвестора меньше при приобретении облигации Z.








