Лекция 12-13. Стандартизация показателей.

Дата: 2025-06-02; Просмотры: 6

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Вопросы:

1. Стандартизованные показатели. Понятие. Особенности.
2. Прямой метод стандартизации
3. Косвенный метод стандартизации
4. Обратный метод стандартизации

1. Стандартизованные показатели. Понятие. Особенности.

Интенсивные коэффициенты правильно отражают частоту распространения явления лишь в том случае, если состав сравниваемых коллективов однороден. Если же сравниваемые совокупности (населения, рабочих, больных и т.д.) имеют неоднородный возрастно-половой или профессиональный состав, различие по тяжести болезни или другим признакам, то наиболее правильным видом анализа является сопоставление специальных коэффициентов частоты, например повозрастных коэффициентов заболеваемости или смертности.

Однако часто в сравниваемых группах наблюдаются противоречивые данные: уровень показателей в некоторых возрастных подгруппах первой группы может быть низким, а во второй группе другие возрастные подгруппы , наоборот, характеризуются более низкими показателями. Во всех подобных случаях прибегают к методу стандартизации, т.е. к устранению, элиминации влияния состава (структуры) совокупностей на общий итоговый показатель. Метод стандартизации применяется тогда, когда имеющиеся различия в составе сравниваемых групп могут повлиять на размеры общих коэффициентов. Для того, чтобы устранить влияние неоднородности составов сравниваемых совокупностей на величину получаемых коэффициентов, их приводят к единому стандарту, т.е. при этом условно допускается, что состав сравниваемых групп одинаков. Стандартизированные коэффициенты показывают, каковы были бы общие интенсивные показатели, если бы на их величину не оказывала влияние неоднородность в составах сравниваемых групп и применяются тогда, когда имеющиеся различия в составе сравниваемых коллективов могут повлиять на размеры общих коэффициентов.. Стандартизированные коэффициенты являются условными величинами и применяются исключительно в целях сравнения.

Целесообразным представляется выбор стандарта, близкий по существу к сравниваемым совокупностям, или в качестве стандарта принять состав одной из них. В настоящее время широко используется Мировой стандарт WORLD и Европейский стандарт. При изменении взятого стандарта изменяются и стандартизированные коэффициенты. Поэтому при анализе следует акцентировать внимание не на абсолютные значения коэффициентов, а на степень различия коэффициентов между собой.

2. Прямой метод стандартизации

Этот метод можно применять в том случае, когда известен возрастной состав населения, а также повозрастные коэффициенты.

Входные данные:

А1₁, А1₂,………… А1_n, А1_общ - число случаев заболевания по возрастам в группе 1.

А2₁, А2₂,………… А2_n, А2_общ - число случаев заболевания по возрастам в группе 2.

N1₁, N1₂,………… N1_n, N1_общ - повозрастная численность населения в группе 1.

N2₁, N2₂,………… N2_n, N2_общ - повозрастная численность населения в группе 2.

Стандарт:

S₁, S₂,………… S_n, S_общ } – повозрастная структура населения.

1 этап. Вычисление повозрастных интенсивных коэффициентов в каждой из сравниваемых групп.

IR1_{1 =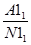} ; IR2_{1 =} ;

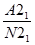IR1_{n =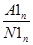} ; IR2_{n =} ;

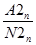IR1_{общ =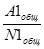} IR2_{общ =}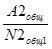

2 этап. Вычисление «ожидаемых» чисел заболевших с учетом повозрастных показателей заболеваемости , присущим группам 1 и 2 при условии, что их возрастная структура соответствует стандарту.

О1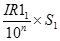₁₌ О2₁₌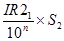

О1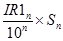_{n =} О2_{n =}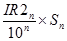

3. Косвенный метод стандартизации.

Применяется, если специальные коэффициенты в сравниваемых коллективах неизвестны или известны, но мало достоверны. Это наблюдается, например, когда числа заболевших очень малы и, следовательно, вычисляемые коэффициенты будут существенно меняться в зависимости от прибавления одного или нескольких случаев наблюдений.

Для расчета стандартизованных коэффициентов косвенным способом входными являются:

1. Повозрастная численность населения в каждой из сравниваемых групп (N1……Nn, Nобщ1), (N2……..Nn,Nобщ2)

2. Число случаев заболевания в каждой из сравниваемых групп за изучаемый период. (А1,А2).

За стандарт в косвенном методе принимают повозрастные коэффициенты

заболеваемости условной болезнью на 100000 населения, принятого за стандарт, т.е за стандарт берутся специальные коэффициенты какого-то хорошо изученного коллектива.

Пусть за стандарт приняты повозрастные коэффициенты (S1…….Sn, Sобщ), тогда, допуская, что повозрастные коэффициенты заболеваемости в обоих сравниваемых группах равны стандартным, определяем, сколько бы заболело людей в каждой возрастной группе, те рассчитывает «ожидаемое» число заболевших (О1………Оn) и (О2………Оn) для каждой сравниваемой группы . Вычисления производим следующим образом:

заболеваемость населения в

«ожидаемое» число заболевших число населения данной ´ населенном пункте, при-

возрастной группы нятом за стандарт

(данной возрастной группы) = -------------------------------------------------------------------

100 000

N1 x S1 N2 x S2 Nn x Sn

O1 = -------------------------------; O2 = --------------------, ……. On = -------------------

100 000 100 000 100 000

Такие же вычисления проводим для другой группы, находя (О2…….Оn). Суммируя полученные значения , получаем соответственно Ообщ1 и Ообщ2.

Далее вычисляются стандартизованные коэффициенты заболеваемости населения.. Для этого действительное число заболевших относят к суммарному «ожидаемому» числу и результат умножают на общий коэффициент заболеваемости стандарта:

(А1/Ообщ1) х Sобщ1; и (А2/Ообщ2) х Sобщ2

Далее производим анализ полученных результатов:

А1 А2

фактическая заболеваемость в группе1 = ---------------, в группе 2 ----------

N общ1 N общ2

Если фактическая заболеваемость в группе 1 больше, чем в группе 2 и стандартизованный коэффициент в группе 1 больше, чем в группе 2, то заболеваемость на самом деле выше в группе 1 , где отмечается однородный состав населения.

Если же фактическая заболеваемость в группе 1 больше, чем в группе 2, а стандартизованный коэффициент в группе 1 меньше чем в группе 2, то заболеваемость на самом деле выше в группе 2, а высокий фактический коэффициент в группе 1 был следствием влияния неоднородной возрастной структуры в этой группе.

4. Обратный метод стандартизации

Для расчета стандартизованных коэффициентов обратным способом входными данными должны быть:

1. Число случаев заболеваний по возрастам в каждой из сравниваемых групп (С1……Сn, Собщ1), (С2……..Сn,Собщ2)

2. Общее число населения в каждой из сравниваемых групп за изучаемый период. (N1,N2).

За стандарт в обратном методе принимают повозрастные коэффициенты

заболеваемости условной болезнью на 100000 населения, принятого за стандарт, т.е за стандарт берутся специальные коэффициенты какого-то хорошо изученного коллектива.

Пусть за стандарт приняты повозрастные коэффициенты (S1…….Sn, Sобщ)

Далее вычисляем «ожидаемую» численность населения сравниваемых групп (О1………..Оn) и (О2……….On), при этом допускается, что повозрастные коэффициенты заболеваемости были такими же , как в группе, принятой за стандарт.

Для вычисления «ожидаемой» численности населения делим число заболевших в каждой возрастной группе на соответствующие повозрастные коэффициенты заболеваемости принятого за стандарт населения и результат умножаем на 100 000.

число заболевших в каждой возрастной группе

«Ожидаемое» число населения =---------------------------------------------------------------- х 100 000

повозрастной коэффициент заболеваемости в

группе , принятой за стандарт

C1 Cn C2 Cn

О1 = --------------- х 100000,………..On = --------- x 100000; O2=----------- x100000…….On=----------- x 100000

S1 Sn S2 Sn

Суммируем О1…….Оn; и О2………Оn.Получаем «ожидаемое» общее число населения в каждой группе (Ообщ1, Ообщ2).

Для устранения различия «ожидаемых» и фактических чисел заболевших, вызванного различием действительных и принятых за стандарт повозрастных коэффициентов заболеваемости, делим общие «ожидаемые» числа заболевших на фактические и умножаем на принятый за стандарт общий коэффициент заболеваемости.

Общее «ожидаемое» число населения

------------------------------------------ х общий коэффициент заболеваемости стандарта

Фактическое число населения

Ообщ1 Ообщ2

---------- х S общ, --------- x Sобщ

N1 N2

Рассчитываем общие интенсивные коэффициенты в каждой группе.

Собщ1 Собщ2

Ф1 =--------, Ф2 = --------

N1 N2

Если фактическая заболеваемость в группе 1 больше, чем в группе 2 и стандартизованный коэффициент в группе 1 больше, чем в группе 2, то заболеваемость на самом деле выше в группе 1 , где отмечается однородный состав населения.

Если же фактическая заболеваемость в группе 1 больше, чем в группе 2, а стандартизованный коэффициент в группе 1 меньше чем в группе 2, то заболеваемость на самом деле выше в группе 2, а высокий фактический коэффициент в группе 1 был следствием влияния неоднородной возрастной структуры в этой группе

Литература

1. Милютин А.А., Дудинская Р.А.Методы обработки информации, МИР им.А.Сахарова, Минск, 1999, 63 с.

2. Марченко Б.И. Здоровье на популяционном уровне: статистические методы

исследования. Таганрог: «Сфинкс». 1997. с.425.

3. Урбах В.Ю. Статистический анализ в биологических и медицинских исследованиях. –М.: Медицина,1975. –296 с.