Лекция 11. Непараметрические методы в эпидемиологии.
Вопросы:
- Коэффициент асимметрии.
- Критерий Пирсона
- Критерий знаков
4. Парный критерий Вилкоксона
1. Коэффициент асимметрии
Изучаемые эпидемиологией явления чаще носят характер нормального распределения. При этом из всех вариант подавляющее большинство составляют варианты среднего размера, и чем дальше они отклоняются от среднего значения признака, тем реже встречаются в данной совокупности. В симметричном вариационном ряду, соответствующем нормальному распределению, значения средней арифметической, моды и медианы совпадают.
В случаях, когда какие-либо причины благоприятствуют появлению значений признака (например, правильно выполненные профилактические мероприятия уменьшают количество заболевших, наличие агрессивных факторов окружающей среды способствует увеличению заболеваемости и т.д.), отличающихся от среднего значения в сторону уменьшения или увеличения, образуются асимметричные распределения. В таких рядах средняя арифметическая, мода и медиана не совпадают. Асимметрия может быть учтена при помощи коэффициента асимметрии (АS), который вычисляется по формуле:
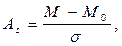
где АS - коэффициент асимметрии, М - средняя арифметическая, Мо - мода, s - среднее квадратическое отклонение. Этот показатель колеблется от -3 до +3.
В медико-биологических исследованиях для оценки значимости различий между двумя эмпирическими совокупностями применяются критерии, не требующие вычисления средних значений, стандартного отклонения и т.д. При применении таких критериев обычно сравниваются не сами варианты, а их порядковые номера (ранги) в ранжированном ряду. Поэтому эти критерии получили название непараметрических или порядковых (ранговых). Основные преимущества непараметрических критериев перед параметрическими следующее:
1. применение этих критериев не связано с определенной формой распределения, что имеет особое значение при малых выборках;
2. меньшая трудоемкость вычислений;
3. некоторые непараметрические методы позволяют оценивать совокупность с полуколичественной характеристикой данных.
2. Критерий Пирсона
В исследованиях, где оценивается близость двух распределений, т.е. там, где явления представлены в виде динамических рядов, целесообразно применять критерий соответствия (согласия), предложенный Карлом Пирсоном и обозначаемый c 2
Основным преимуществом критерия c2 является то, что он одним числом может выразить степень соответствия многих выборочных совокупностей. Значение критерия c2 является положительным числом, которое тем больше, чем больше несоответствие между сравниваемыми совокупностями (рядами) наблюдений. При полном отсутствии различия между ними величина критерия c2 будет равна нулю (не случайно при этом говорят о справедливости "нулевой гипотезы", гипотезы об отсутствии значимых различий между сравниваемыми совокупностями).
Предполагаем, что проживание детей вдали/вблизи промышленных предприятий не влияет на состояние системы ЖКТ (нулевая гипотеза).
Зависимость между местом проживания (вблизи/вдали заводов) и наличием патологии ЖКТ.
| Дети | С патологией ЖКТ | Без патологии ЖКТ | Итого |
| Проживающие вблизи заводов | 15(а) | 32(b) | 47( a+b) |
| Проживающие вдали заводов | 37(с) | 56(d) | 93( c+d) |
| Всего | 52 (a+c) | 88 (b+d) | 140 (a+b+c+d) |
На основании первичной таблицы составляется макет таблицы 2х2
Вычисление в данном случае можно вести по формуле:
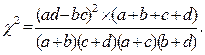
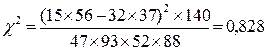
Для того, чтобы мы могли отвергнуть "нулевую гипотезу", вычисленная величина c2 должна быть больше табличного (критического) значения c2 (1)(Приложение, табл. 1) при уровне значимости р=0,05. При этой оценке учитывается число степеней свободы, т.е. число "свободно варьирующих" элементов или число клеток таблицы, которые могут быть заполнены любыми числами без изменения общих итоговых цифр. В нашем примере мы имеем четырехклеточную таблицу и одну степень свободы, так как после нахождения одного "ожидаемого" числа три остальные можно получить как дополнение до итоговых чисел. Для нахождения числа степеней свободы можно также применять формулу: 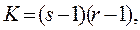
где s - число граф первоначальной таблицы (без графы "итого"); r - число строк таблицы (без строки "всего").Как видно из таблицы (Приложение, табл.1), когда число степеней свободы К=1, критическое значение c2 для уровня значимости р=0,05 равно 3,84; для уровня значимости р=0,01 - 6,63; для р=0,001 - 10,8. Так как вычисленная величина c2 (0,828) меньше 3,8, то следует принять «нулевую гипотезу». Таким образом, можно утверждать, что проживание вблизи/вдали заводов не влияет на заболеваемость ЖКТ. Необходимо подчеркнуть, что критерий c2 должен всегда определяться на основании абсолютных, а не относительных чисел.
3. Критерий знаков
Принцип метода критерия знаков заключается в подсчете числа однонаправленных эффектов в попарно сопряженных вариантах. Этот метод находит широкое распространение при ретроспективном анализе. При рассмотрении годовых показателей заболеваемости ювенильным ревматоидным артритом среди детского населения в двух областях Республики Беларусь оказалось, что в Гродненской области в трех случаях из пяти заболеваемость была выше, чем в Минской области Нулевая гипотеза заключается в том, что Гродненская и Минская области по уровню заболеваемости не различаются. Чтобы ее отвергнуть, максимальное число менее часто встречающихся знаков при данном числе вариант(8) должно быть равно 1, а в нашем случае – 2 (1) (приложение 1 , табл.3)
| Год | Гродненская область | Минская область | Разность | Ранг абсолютного значения разности | Ранг меньшего числа однозначных разностей |
| 1985 | 64 | 69 | -5 | 3 | 3 |
| 1987 | 66 | 65 | 1 | 1 | |
| 1989 | 73 | 76 | -3 | 2 | 2 |
| 1992 | 99 | 82 | 17 | 4 | |
| 1995 | 126 | 91 | 35 | 5 |
т.е. по критерию знаков различия в двух рассматриваемых выборках не являются существенными.
4. Парный критерий Вилкоксона(критерий Т)
Установленным разностям в попарно сопряженных показателях присваивают номера (ранги) в порядке возрастания абсолютных значений разности (без учета знака). Далее определяется значение Т, равное сумме ранговых номеров менее часто (по знаку) встречающихся разностей. Сравниваем полученное значение с табличным (приложение, табл.2). Если полученное значение Т больше критического для данного n, нулевая гипотеза принимается. В нашем случае менее часто встречающиеся (по знаку) имели ранговые номера 2 и 3. Таким образом, Т=2+3=5. Это больше 0 . Анализ заболеваемости двух динамических рядов с помощью критерия Т достоверных различий не выявил.
Литература
1. Милютин А.А. Дудинская Р.А. Методы обработки информации.МИР им.А.Сахарова, Минск, 1999, 63с.
2. Лванга С.К., Чжо-Ек Тыэ. Обучение медицинской статистике, ВОЗ. Женева. 1989. 216 с.








