– коэффициент влияния подложки.

Дата: 2025-06-02; Просмотры: 16

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Коэффициент влияния подложки демонстрирует насколько пороговое напряжение чувствительно относительно обратного смещения на подложку. Поскольку 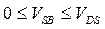, логично в качестве среднего значения выбрать 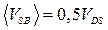. Тогда (см. (3.3.3)):

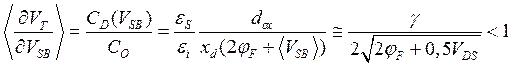, (3.5.2)

где 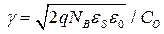(см. (3.3.2)).

Отметим, что коэффициент влияния подложки п по смыслу и значению очень близок введенному в п. 3.1 безразмерному коэффициенту т:

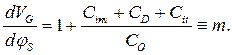
Считая коэффициент влияния подложки постоянной величиной ( 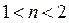), можно приближенно рассчитать распределение плотности носителей вдоль канала

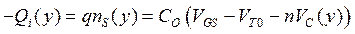. (3.5.3)

Плотность электронов у истока ( 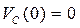) в этом приближении постоянна: 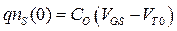, а вблизи стока ( ):

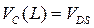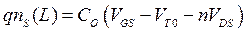. (3.5.4)

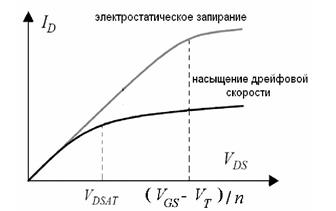
При некотором значении 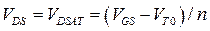, которое называется напряжением насыщения, плотность электронов в канале вблизи стока оказывается формально равной нулю. Это исчезновение инверсного слоя вблизи стока называется перекрытием канала или электростатическим запиранием. Дополнительное напряжение на стоке (превышающее напряжение насыщения) 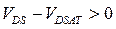падает на рп-переходе стока и практически перестает влиять на распределение потенциала в канале. Это означает, что зависимость тока в канале от напряжения V_DS насыщается, то есть ток практически перестает расти.

3.6. Простейшая модель ВАХ МОПТ

Пренебрегая диффузионной составляющей тока, полный ток в канале шириной Z можно записать в виде

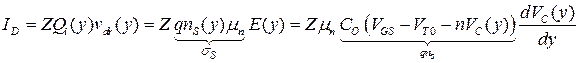(3.6.1)

Здесь Z(cм), 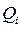(Кл/см²), 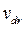(см/с), μ _n (см²/В∙с), Е (В/см). Последнюю формулу можно переписать в форме

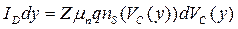. (3.6.2)

С учетом (3.5.3)[6], обе стороны уравнения (3.6.2) можно проинтегрировать с граничными условиями

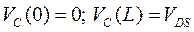. (3.6.3)

Формальный интеграл от (3.6.2) дает выражение

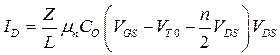, (3.6.4)

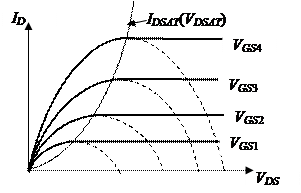в котором при 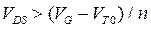ток начинает уменьшаться с ростом V_DS (рис. 3.4, штриховые линии). Однако такое поведение физически неприемлемо, поскольку, как следует из (3.5.3), отрицательный заряд в канале существует только при 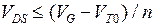,то есть только при напряжении 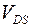меньше напряжения насыщения.

Рис. 3.4. Схематические выходные ВАХ МОПТ для разных напряжений на затворе

В качестве тока насыщения принято использовать максимальное значение (3.6.4). То есть ток насыщения транзистора I_DSAT вводится с помощью процедуры нахождения экстремума функции:

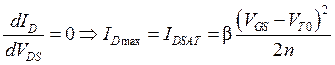(3.6.5)

при 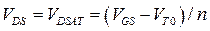- напряжение насыщения, после которого ток насыщается

Таким образом, в этом простейшем приближении вольтамперная характеристика (ВАХ) МОПТ выражается кусочно-непрерывной функцией

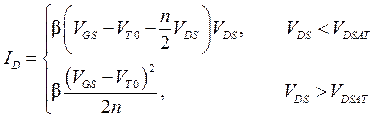, (3.6.6)

где 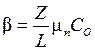− удельная крутизна МОПТ.

С увеличением 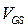величина 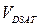растет: каждому 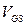соответствует свое напряжение насыщения 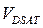. Область ВАХ, в которой 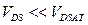, называется линейной или омической областью. Область ВАХ, в которой 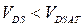, называется крутой областью, а область ВАХ с 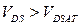называется областью насыщения или пологой областью.

Это базисное уравнение (3.6.6), полученное еще в начале 60-х гг. ХХ в., до сих пор остается основой практически для всех моделей, используемых в модифицированном виде, в том числе и для проектирования наноэлектронных МОПТ с длиной канала < 100 нм. Причина этого состоит в том, что ВАХ транзисторов, в том числе самых современных, имеют довольно простой вид, и для их описания достаточно (особенно при использовании множества подгоночных параметров) использования простых компактных моделей, не требующих громоздких расчетов.

3.7. Насыщение скорости носителей в канале

При выводе выражения для ВАХ МОПТ мы считали, что подвижность носителей в канале является константой. На деле подвижность определяется многими параметрами и, в частности, зависит от величины электрического поля вдоль канала Е(у).

С ростом тянущего электрического поля рассеяние носителей в канале усиливается, и дрейфовая скорость насыщается на своем максимальном уровне порядка тепловой скорости носителей в канале (рис. 3.5)

v_T ~ 10⁷ см/с. (3.7.1)

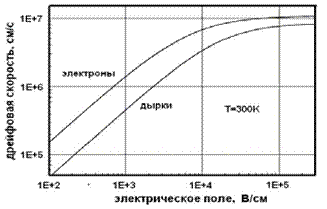
В КНИ (кремний на изоляторе) транзисторах основным механизмом насыщения дрейфовой скорости, как и в объемном случае, является интенсивное рассеяние на оптических фононах. Тем не менее, в КНИ транзисторах с ультратонким телом существенную роль начинает играть рассеяние на границах раздела (см. рис. 3.6).

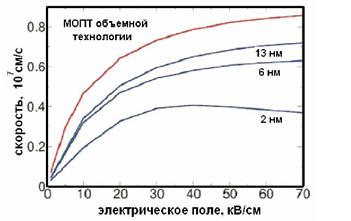
Хорошая количественная физическая модель зависимости подвижности от тянущего поля в каналах отсутствует, и поэтому широко используются эмпирические модели. Например, зависимость дрейфовой скорости носителей от тянущего поля v_dr(Е) приближенно аппроксимируется формулой

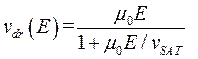, (3.7.2)

где 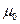− подвижность носителей в канале транзистора в слабых тянущих полях; v_SAT − скорость насыщения носителей в канале транзистора.

Типичные значения скоростей насыщения в каналах МОПТ

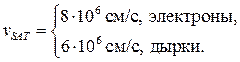(3.7.3)

Вместо скорости насыщения часто используют значение электрического поля, соответствующего насыщению E_SAT , иногда определяемого как

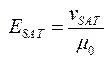. (3.7.4)

Практика показывает, что использование соотношения (3.7.2) совместно с формулой (3.7.4) (условно говоря, модель 1) соответствует относительно медленному нарастанию дрейфовой скорости и приводит к ее недооценке при промежуточных значениях тянущих электрических полей (рис. 3.7).

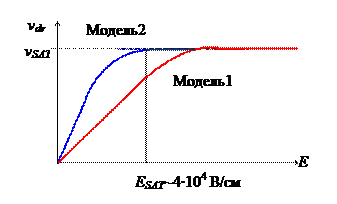
Поэтому на практике чаще всего используется, условно говоря, модель 2, в которой параметр электрического поля насыщения определяется как

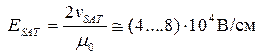, (3.7.5)

а зависимость дрейфовой скорости от тянущего поля представляется линейно-кусочным выражением

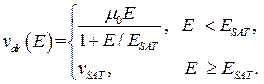(3.7.6)

В отличие от модели 1, где 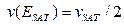, модель 2 дает 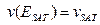, и соответствует более быстрому насыщению скорости, что лучше согласуется с экспериментальными данными.

3.8. Механизмы насыщения тока канала

Таким образом, насыщение тока в канале МОПТ может происходить за счет двух физически различных механизмов.

A. Электростатическое запирание канала

Насыщение тока в данной модели достигается за счет электростатического запирания канала (перекрытие канала), которое начинается, когда плотность носителей в канале на границе со стоком становится равной нулю (см. 3.5.4):

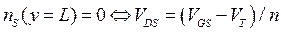. (3.8.1)

Ток насыщения в канале (см. (3.6.6)) в этом случае можно представить в виде произведения средней плотности заряда в канале на максимальную дрейфовую скорость, зависящую в этом случае только от затворного напряжения:

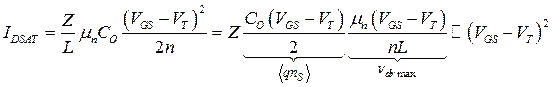(3.8.2)

Б. Насыщение дрейфовой скорости

Согласно экспериментальным данным, отраженным в эмпирической формуле

(3.7.2), при достаточно сильных полях в канале дрейфовая скорость носителей насыщается вне зависимости от затворного напряжения. Это означает, что при выполнении неравенства

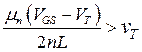
ток насыщения в канале можно представить в виде

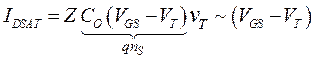. (3.8.3)

С физической точки зрения это означает, что все носители в канале движутся с максимальной скоростью, близкой к их тепловой скорости 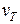. Современные цифровые ИС работают с максимальной дрейфовой скоростью, и для оценки их максимального тока более подходит формула (3.8.3).

Характер насыщения легко определить из вида ВАХ. При электростатическом запирании, характерном для длинноканальных транзисторов, имеет место традиционная квадратичная зависимость

~ .

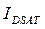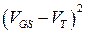Для короткоканальных транзисторов с насыщением дрейфовой скорости имеем

~ .

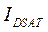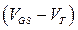В реальности в современных приборах экспериментально наблюдается, как правило, промежуточная ситуация, когда зависимости тока насыщения от затворного напряжения имеют вид

~ ,

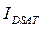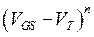где .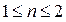

3.9. ВАХ МОП-транзистора с учетом насыщения дрейфовой скорости

Итак, уменьшение подвижности и насыщение дрейфовой скорости при возрастании тянущего электрического поля в канале приводит к появлению дополнительного механизма насыщения тока в канале МОПТ. Рассчитаем ВАХ МОП транзистора с учетом возможного насыщения дрейфовой скорости. Как и в случае длинноканальных транзисторов с электростатическим запиранием, распределение плотности электронов вдоль канала при малом смещении между стоком и истоком V_DS < V_G − V_T записывается в виде (см. (3.5.3))

.

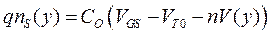Начальное уравнение для дрейфового тока записывается в том же виде, как и в (3.6.1)

,

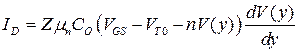но только с учетом зависимости подвижности от тянущего поля (3.7.2):

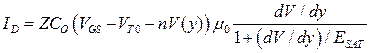. (3.9.1)

Эту формулу можно переписать в форме

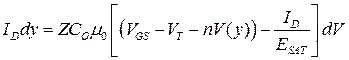(3.9.2)

и проинтегрировать обе стороны полученного уравнения от истока (у = 0) до стока (у = L):

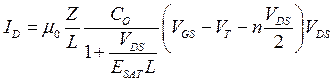. (3.9.3)

Когда L велико, выражение (3.9.3) сводится к (3.6.6). Последняя известна как длинноканальная модель:

.

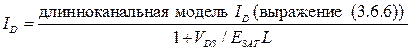Влияние насыщения скорости сводится к уменьшению 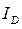с коэффициентом 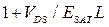. Этот коэффициент сводится к 1 (то есть насыщением скорости пренебрегается), когда 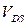мало или 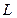велико. Этот коэффициент можно интерпретировать как 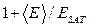, где 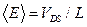− среднее поле в канале.

Ток насыщения можно определить, приравнивая как и ранее, производную к нулю (dI_D / dV_DS = 0), что дает напряжение насыщения:

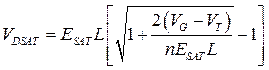. (3.9.4)

Подставляя (3.9.4) в выражение для тока (3.9.3), можно получить формулу для тока насыщения МОПТ. Полученная при этом формула имеет очень громоздкий вид. Поэтому часто используют более простой и, как оказалось, более точный способ определения напряжения насыщения (аппроксимация):

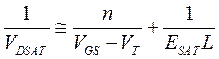. (3.9.5)

Если 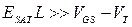, то вторым слагаемым в (3.9.5) и эффектами насыщения дрейфовой скорости можно пренебречь, и насыщение тока происходит только за счет электростатического запирания:

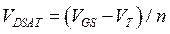. (3.9.6)

Такая ситуация имеет место для длинноканальных МОПТ (когда L велико) и/или когда V_GS чуть больше V_T (мал овердрайв).

В противном случае, когда ,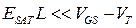

,

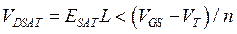и насыщение тока МОПТ происходит за счет насыщения скорости носителей в канале МОПТ. Соответственно, ток насыщения МОПТ представляется в виде формулы

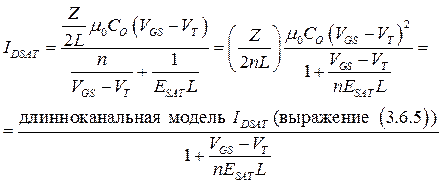. (3.9.7)

В зависимости от соотношения параметров, получаются предельные случаи (рис. 3.8) насыщения дрейфовой скорости :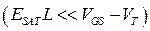

;

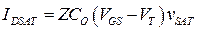и электростатического запирания канала :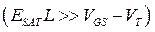

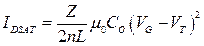
Литература:

1. Зебрев Г.И. Физические основы кремниевой наноэлектроники, М.: БИНОМ, 2011, с. 85-103

2. Парменов Ю.А. Элементы твердотельной наноэлектроники. Учебное пособие. М.: МИЭТ, 2011, гл. 3.

3. Красников Г.Я. Конструктивно-технологические особенности субмикронных МОП-транзисторов. М., Техносфера, 2011.

4. Taur Y., Ning T.H., Fundamentals of Modern VLSI Device, 2009, p. 148-201.

5. Sze S.M., Ng К.К., Physics of Semiconductor Devices, Wiley, 2007, p. 293-343.

Задание для СРС

1.Изучить материал лекции №3 по конспекту и по литературным источникам.

2. Для подготовки к следующей лекции ознакомиться с её материалом по конспекту лекции №4. При подготовке рекомендуется восстановить в памяти знания по физике работы МДП-транзисторов по книге
В.И. Старосельский «Физика полупроводниковых приборов микроэлектроники». - М : Высшее образование, Юрайт-Издат, 2009, с.133-253. Обратить особое внимание на физику короткоканальных эффектов.

Вопросы для самопроверки

1. Запишите выражения для подпорогового тока.

2. Что такое подпороговый размах напряжения (S-фактор)?

3. Чему равно минимально возможное (идеальное) значение S-фактора?

4. Какова связь подпорогового тока утечки с пороговым напряжением?

5. Как изменяется пороговое напряжение МОПТ при приложении обратного смещения на подложку?

6. Что такое коэффициент влияния подложки? От чего он зависит?

7. Запишите выражения для распределения плотности носителей вдоль канала с учетом коэффициента влияния подложки.

8. Запишите выражение для вольтамперной характеристики МОПТ в приближении плавного канала.

9. Как зависят дрейфовые скорости электронов и дырок от электрического поля в кремнии?

10. Каковы механизмы насыщения тока в канале МОПТ?

11. Нарисуйте и сравните выходные ВАХ длинноканального и короткоканального МОПТ.

[1]

[2] (2.7.4)

[3] (2.2.8)

[4] (2.2.5)

[5] (3.3.3)

[6] . (3.5.3)