Найти аналитическое решение системы нелинейных уравнений относительно величин x, y и z.. Поведение функций x( d), y( d) и z( d) представить графически.

Дата: 2025-06-14; Просмотры: 7
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

 

Формат использования в данном случае функции Find для получения решения в аналитическом виде приведён в программе решения задачи 2m. Основной отличительной особенностью по сравнению с использованием функции Find в режиме численных вычислений, в режиме аналитических вычислений никаких начальных значений искомых величин не задаётся. Для графического представления зависимостей исходя из результатов вычислений необходимо создать функции пользователя x( d), y( d) и z( d), а затем задать диапазон изменения переменной d.

 

MathCad программа решения задачи 3m

 

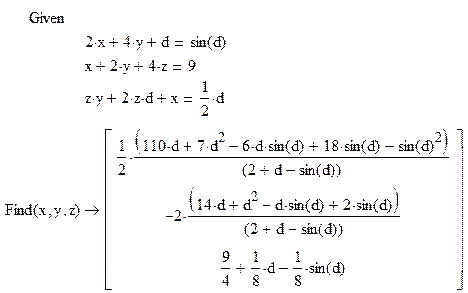
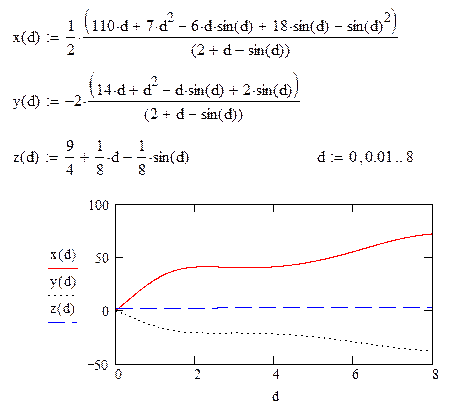
Автоматически представить полученный результат в виде соответствующих функций пользователя x( d), y( d) и z( d) позволит следующий приём:
Rez(d): = Find(x,y,z)®, задав функции пользователя следующим образом:
x(d): = Rez(d)0 .

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

 

  1. На какие группы делятся методы компьютерного решения систем линейных алгебраических уравнений?
  2. Какие средства предоставляет среда MathCad пользователю для решения СЛАУ?
  3. Как изменить количество значащих цифр после точки, при выводе результатов на экран в MathCad?
  4. Как вставить комментарий в MathCad – документ?
  5. Какие встроенные переменные среды MathCad Вы знаете?
  6. Формат использования функции Find.

 

литература

1. Очков В.Ф. Mathcad PLUS 6.0. для студентов и инженеров. - М.: ТОО фирма “Компьютер Пресс”, 1996 г. - 238 с.

2. Гулд Х., Тобочник Я. Компьютерное моделирование в физике: в 2-х частях. Пер. с англ. - М.:Мир, 1990 г.

3. А. Е. Мудров Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. – Томск: МП «РАСКО», 1991. 272 с.

4. М. Херхагер, Х. Партолль MathCad 2000 : полное руководство. Пер. с нем. - К. : Издательская группа BHV, 2000, - 416 с.

5. Дьяконов В.П., Абраменкова И.В. MathCad 7.0 в математике, физике и в Internet. - М.: «Нолидж», 1999. - 352 с.

6. Очков В.Ф. Mathcad 7 PRO для студентов и инженеров. - М.: “Компьютер Пресс”, 1998 г. - 384 с.

7. Бородич Л.И., Герасимович А.И., Кеда Н.П., Мелешко И.Н. Справочное пособие по приближенным методам решения задач высшей математики. - Мн.: Высшая школа, 1986. - 189 с.

8. Кирьянов Д.В. Самоучитель MathCad 11. – СПб.: БХВ – Петербург, 2003.