Задана система линейных алгебраических уравнений
ЛАБОРАТОРНАЯ РАБОТА № 3
системы линейных алгебраических уравнений
Цель работы: изучение методов решения систем линейных алгебраических уравнений в среде MathCad. Получение навыков решения систем линейных алгебраических уравнений.
ВВЕДЕНИЕ
Решение ряда задач сводится к решению системы линейных алгебраических уравнений, причем, данные задачи являются вспомогательными при реализации многих алгоритмов решения задач математической физики, обработки данных экспериментальных исследований.
Методы численного решения систем линейных алгебраических уравнений (СЛАУ) делятся на две группы: прямые и итерационные. В прямых методах решение СЛАУ находится за конечное число арифметических действий.
Итерационные методы (их называют методами последовательных приближений) состоят в том, что решение СЛАУ находится как предел последовательных приближений х(n), где n - номер итерации. Как правило, за конечное число итераций этот предел не достигается. Обычно задается некоторое малое число e>0 (точность) и вычисления проводятся до тех пор, пока не будет выполнено условие | х(n)- х|<e.
Запишем исходную систему линейных алгебраических уравнений в общем виде:
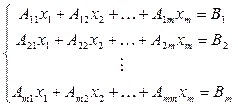(1)
В матричной записи система (1) выглядит следующим образом A × X=B, отсюда
X=A-1 ×B (2). Простейший способ решения системы линейных алгебраических уравнений в MathCad реализуется с помощью матриц: X:=A-1.B , где А - матрица коэффициентов, а В - матрица-столбец свободных членов системы уравнений. Аналогичный результат получается с использованием функции системы MathCad lsolve(A,B). Встроенная системная переменная ORIGIN используется для задания нумерации элементов матриц и векторов, отличной от установленной по умолчанию. Значение переменной ORIGIN установленное по умолчанию в MathCad - 0.
задача 3.
Задана система линейных алгебраических уравнений
.
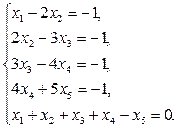Необходимо найти решение данной системы.
Для решения данной задачи может быть успешно использован матричный метод. Для его использования необходимо задать матрицу системы уравнений А и матрицу столбец (вектор) свободных членов системы В. Поместить матрицу в MathCad документ можно воспользовавшись кнопкой вставки матрицы 
инструментальной математической панелью матриц и векторов .
MathCad программа решения задачи 3 (матричным методом)
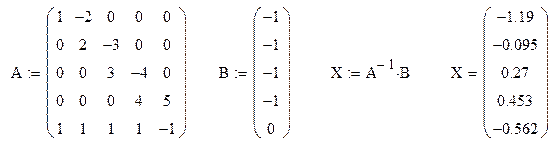
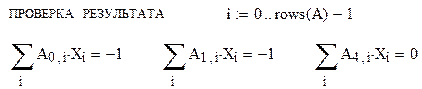
Матрицы А и В могут быть заданы и по другому – посредством задания всех их матричных элементов. Элемент матрицы задаётся путём помещения у имени матрицы индексов, разделённых запятой, соответствующих строке и столбцу элемента. Индекс у имени можно поместить, воспользовавшись кнопкой Xn из инструментальной панели матриц и векторов . Функция rows ( A) позволяет определить число строк матрицы А.
После выполнения вычислений должна проводиться проверка результатов.
Количество значащих цифр, выводимых на экран, можно изменить, воспользовавшись меню Format (Формат)® Number (Результат). (закладка Формат числа).
В любом месте документа пользователь может поместить комментарий, т.е. текстовый блок, поясняющий вычисления, воспользовавшись меню Insert (Вставка)® Text Region (Область текста).
Для решения задачи 3 можно воспользуемся функцией системы MathCad Find, которая предназначена для решения систем линейных и нелинейных алгебраических уравнений. Данная функция работает со служебным словом Given за которым должны следовать уравнения, подлежащие решению. Уравнения должны быть записаны как булевы выражения.
Для работы функции Find необходимо задать начальное приближение искомых переменных, поскольку эта функция работает по итерационному механизму вычислений. При решении систем уравнений переменная Rez является вектором, а Find в этом случае содержит соответствующее число аргументов. При решении данной задачи используется встроенная переменная TOL, которая задает погрешность для итерационных вычислений. Значение переменной TOL, установленное по умолчанию составляет 0.001.
MathCad программа решения задачи 3 (с использованием функции Find)
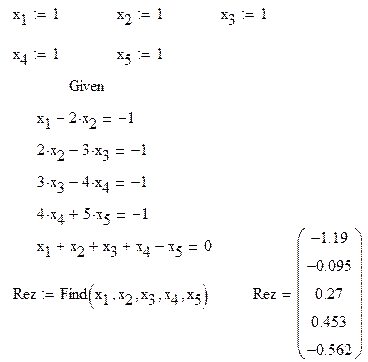
Имена искомых переменных содержат цифровые символы, которые визуально напоминают переменные с индексами. Для того, чтобы в программе создать переменную x1 необходимо после x поставить точку, которая в MathCad документе не отображается, а затем цифру 1.
Следует отметить основные особенности использования функции Find:
1. Решение получаемое с помощью функции Find зависит от начального приближения.
2. Решение получаемое с помощью функции Find зависит от значения переменной TOL.
3. Число уравнений системы может быть достаточно большим.
4. Уравнения системы могут быть нелинейными.
Функция Find, рассмотренная нами ранее, может успешно использоваться и для аналитического решения нелинейных уравнений и их систем. В данном случае начальные приближения искомых величин не задаются. После служебного слова Given, как и ранее, следуют уравнения, а за ними функция Find в виде Find( x, y, z) ® . Рассмотрим задачу 3m.
Задача 3 m