Исследование реактивных электрических фильтров

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Работа №14

ИССЛЕДОВАНИЕ РЕАКТИВНЫХ ЭЛЕКТРИЧЕСКИХ ФИЛЬТРОВ

Цель работы: ознакомление с простыми реактивными фильтрами Баттерворта нижних и верхних частот, полосно-пропускающими фильтрами; исследование свободных процессов реактивных фильтров и их фильтрующих свойств при воздействии периодических несинусоидальных сигналов.

14.1. Подготовка к работе

Электрический фильтр – это четырехполюсник, который пропускает частотные составляющие сигнала, лежащие в некотором диапазоне частот, называемом полосой пропускания (ПП), и задерживает частотные составляющие, лежащие вне этого диапазона – в полосе задержки (ПЗ).

В работе используются фильтры Баттерворта нижних частот (ФНЧ), фильтры верхних (ФВЧ) и полосно-пропускающие фильтры (ППФ) с полосой пропускания, соответственно: 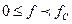, 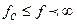и 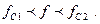Граничные частоты 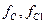и 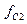между полосой пропускания и полосой задержки называют частотами среза. Фильтры Баттерворта имеют амплитудно-частотную характеристику (АЧХ) максимально плоскую в полосе пропускания и монотонно убывающую в полосе задержки. Эти фильтры относятся к классу полиномиальных фильтров.

Функция передачи простого полиноминального реактивного ФНЧ третьего порядка с тремя нулями в бесконечности имеет вид:

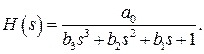(14.1)

Коэффициенты (14.1) определяются из условия приближения амплитудно-частотной характеристикой 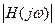к заданной в виде прямоугольника – идеальной характеристики ФНЧ

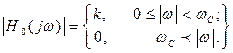(14.2)

Характеристика 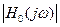изображена на рис. 14.1, б в виде прямоуголь-ника тонкой пунктирной линией.

Рассмотрим приближение с помощью простейшего метода Тейлора (фильтры Баттерворта). Квадрат АЧХ функции передачи (14.1)

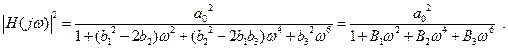(14.3)

Делением числителя на знаменатель получаем разложенный степенной ряд:

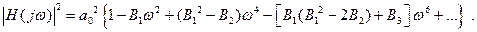(14.4)

С другой стороны, производные при 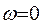идеальной характеристики 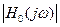равны нулю. Поэтому все коэффициенты ее ряда обращаются в нуль, кроме коэффициента при частоте в нулевой степени: H ₀ (0)= k . Приравняв коэффициенты при ω² и ω⁴ в (14.4) к нулю, получаем B ₁ =0, B ₂ =0, а из равенства 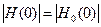имеем a ₀ = k. Если нормировать частоту так, чтобы B ₃ =1, выражение для АЧХ (14.3) ФНЧ Баттерворта n–го порядка принимает вид

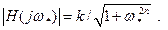
При изменении частоты от нуля до бесконечности АЧХ монотонно спадает от максимального значения k до нуля (рис. 14.1, б). При нормиро-ванной частоте среза 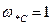значение 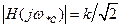. С повышением порядка n фильтра крутизна спада АЧХ в полосе задержки возрастает.

Определив, как указано выше, коэффициенты B ₁ , B ₂ , B ₃ в (14.4), находим b ₃ =1, b ₁ = b ₂ =2; следовательно, функция передачи фильтра

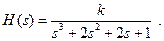(14.5)

Функцию передачи (14.5) необходимо реализовать, т. е. найти схему приемлемой структуры и значение ее элементов (см.: Ю.А. Бычков и др. Основы теории электрических цепей. – СПб.: Издательство “Лань”, 2002).

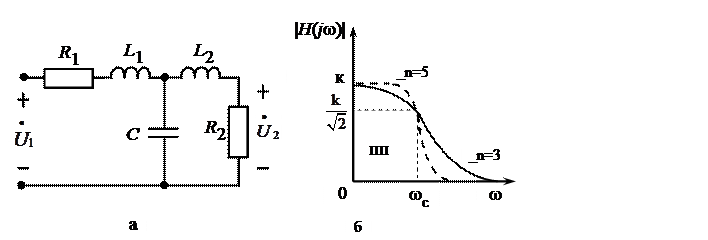
Рис. 14.1

На рис.14.1, а изображена одна из таких схем в виде реактивного Т–образного трехполюсника, нагруженного на входе и выходе на нормированные сопротивления 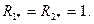Функции передачи такой цепи, называемой ФНЧ – прототипом, имеет вид:

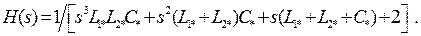(14.6)

Прировняв коэффициенты (14.5) и (14.6), имеем три уравнения для трех нормированных параметров:

; ;

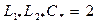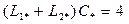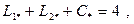
которые дают ; .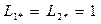

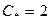Относительный уровень выходного напряжения k=0,5.

Полученные значения параметров относятся к нормированным с частотой среза 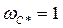и сопротивлениями 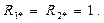Пересчёт пара-метров фильтра нижних частот на заданные параметры входного сопротивления 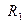и выходного сопротивления 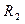, а также частоту среза f_C производят, как обычно, по выражениям

;

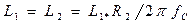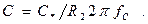
Параметры фильтра верхних частот (ФВЧ) получают по заданной частоте среза 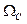, применив частотное преобразование параметров ФНЧ с помощью функции

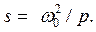(14.6) Из условия пересчета частот среза 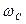и 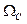находим коэффициент

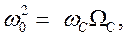(14.7)

а затем на основании (14.6) определяем параметры 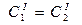и 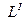схемы ФВЧ (см. рис. 14.2, а) по известным параметрам 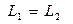и 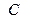схемы ФНЧ:

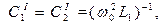
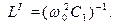(14.8)

Таким образом, по формулам (14.7) и (14.8), зная параметры фильтра- прототипа 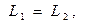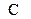и частоту среза 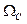, можно рассчитать параметры фильтра верхних частот.

Аналогично можно определить и другие характеристики ФВЧ по данным ФНЧ. На рис. 14.2, б показана амплитудно-частотная характеристика схемы фильтра верхних частот.

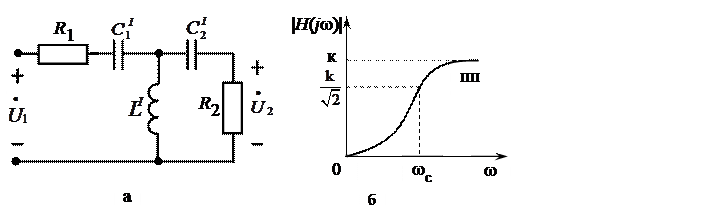
Рис. 14.2

Параметры полосно-пропускающего фильтра (ППФ) получают по заданным частотам среза 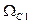и 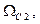применив частотное преобразование параметров ФНЧ с помощью функции

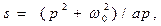(14.9) где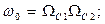

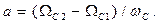
Следовательно, характерная частота ФНЧ 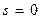преобразуется согласно формулы (14.9) к частоте ППФ 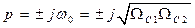и находиться между частотам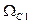и и 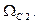Амплитудно-частотная характеристика ППФ показана на рис. 14.3, б. Схема ППФ изображена на рис. 14.3, а.

В случае 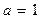значения параметров продольных ветвей схемы, выполненных в виде последовательных 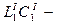контура и 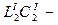контура

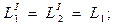
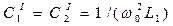
и поперечной ветви, выполненной в виде параллельного 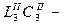контура

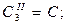
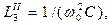
где 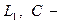параметры элементов схемы ФНЧ.

Рис. 14.3

Для АЧХ фильтров обычно применяют логарифмический масштаб и вводят понятие затухания (коэффициент затухания), измеряемого в децибелах:

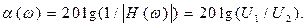(14.10)

Затухание сигнала на выходе фильтра 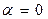при 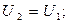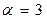дБ при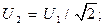 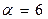дБ при 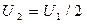и т. д.

На рис. 14.4 показаны, соответственно, характеристики затухания ФНЧ, ФВЧ и ППФ для случая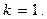

14.2 Экспериментальные исследования

Для начала работы на ЭВМ необходимо открыть каталог Multisim _Work, далее подкаталог Lab_ Rab_14 и файл LC_ Filter. ms7. В открывшемся окне появится схема полосового 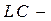фильтра (рис. 14.5) с подключенными к ней измерительными приборами: функциональным генератором XFG1, графопостроителем XBP1 и осциллографом XSC1. Схемы 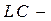фильтров нижних и верхних частот собираются из элементов с помощью шести ключей 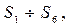управляемыми клавишами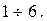

полосового фильтра с помощью шести ключей 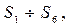управляемыми клавишами

2. Определение частотных характеристик 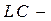фильтра нижних частот

Для выполнения экспериментальных исследований 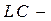фильтра нижних частот активизируйте схему, показанную на рис. 14.5. Для этого подведите курсор к клавише Simulate в командной строке и щелкните по ней с помощью левой клавишей мыши. В открывшемся окне щелкните по клавише Run.

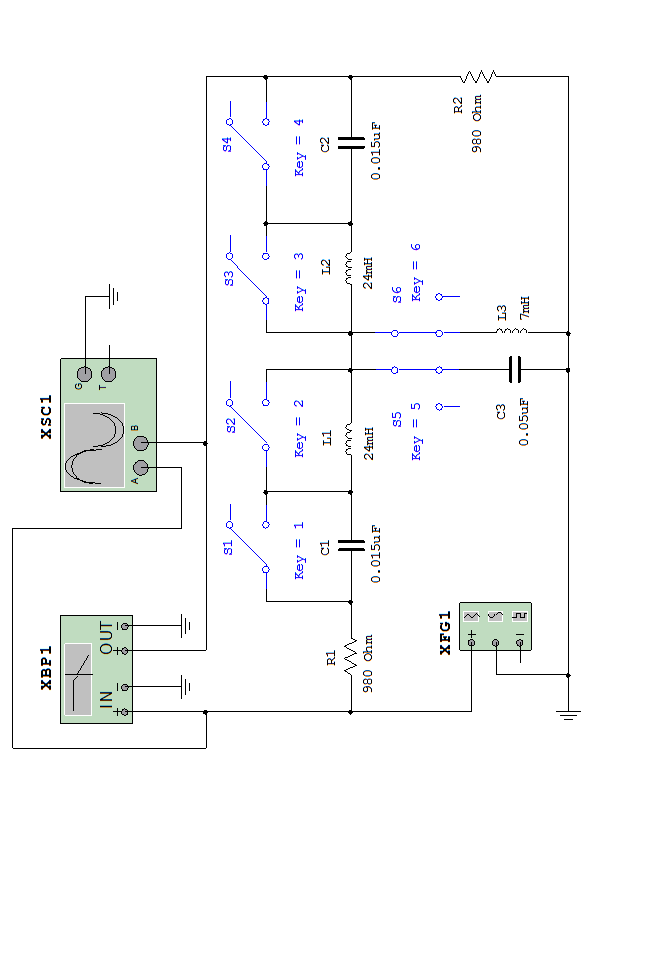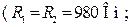
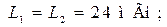
Соберите схему ФНЧ 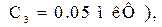показанную на рис. 14.1, а. Подведите курсор к изобра-

жению функционального генератора XFG1 и щелкните по нему два раза левой клавишей мыши. На открывшейся диалоговой панели нажмите кнопку для установления режима генерации синусоидальных сигналов. Установите амплитуду синусоидальных сигналов 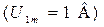в строке Amplitude. Установите в строке Frequency частоту 1 кГц.

Для снятия АЧХ и ФЧХ фильтра нижних частот с помощью графопостроителя XBP1 (Боде плоттер) активизируйте схему. Откройте экран графопостроителя двойным щелчком мыши по его изображению и получите увеличенное изображение. Для получения белого фона экрана графопостроителя нажмите кнопку Reverse.

Для снятия АЧХ фильтра нажмите кнопку Magnitude на верхней панели (Mode) графопостроителя. На правой панели управления (Horizontal) установите необходимый диапазон частот измерения АЧХ:

вид шкалы горизонтальной оси линейная (Lin);

начальное 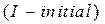и конечное 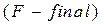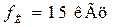значения частот, устанавливаемых по горизонтальной оси;

На левой панели управления (Vertical) установите аналогично линейный масштаб (Lin) отношения напряжений: 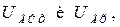а также начальное (I) и конечное (F) значения АЧХ. Эти границы выбираются так, чтобы на экране был виден весь график АЧХ. Снимите АЧХ фильтра в диапазоне частот от 100 Гц до 15 кГц. Для этого нажатием мыши на кнопки со стрелками и расположенными слева и справа от экрана, двигайте курсор по экрану графопостроителя. ”Тащить” курсор по экрану можно также с помощью мыши. Координаты точек пересечения курсора с графиком АЧХ спишите внизу информационного поля. При измерениях обязательно зафиксируйте граничную частоту по­лосы пропускания фильтра, на которой величина АЧХ равно 0,707 от ее максимального значения. Результаты измерений занесите в табл.14.1.

Для снятия ФЧХ фильтра нажмите кнопку Phase на верхней панели (Mode) графопостроителя. Для получения белого фона экрана графопостроителя нажмите кнопку Reverse. На правой его панели управления

(Horizontal) установите линейный диапазон частот от 10 Гц до 15 кГц, а также линейный масштаб величин измерения ФЧХ в пределах от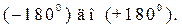

Снимите в указанном диапазоне частот ФЧХ фильтра нижних, перемещая курсор по экрану графопостроителя. При измерениях зафиксируйте значения ФЧХ на границе полосы пропускания фильтра. Результаты измерений занесите в табл.14.1.

Таблица 14.1

Наблюдают			Вычисляют

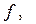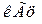
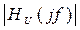
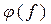
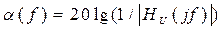
По результатам наблюдений АЧХ и ФЧХ постройте графики и опреде­лите полосу пропускания фильтра. В таблицу также внесите результаты расчета затухания фильтра нижних частот по (14.10). Постройте график затухания фильтра.

Вопросы: I. Как объяснить вид АЧХ, пользуясь эквивалентной схемой реактивного ФНЧ при частотах 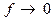и 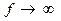? 2. Как изменится АЧХ реактивного фильтра нижних частот, если сопротивление на его входе будет равно нулю? 3. Какие элементы реактивного ФНЧ обеспечивают трехкратный нуль при 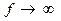? 4. Соответствует ли полученная АЧХ характеристике фильтра Баттерворта ? 5. В чем отличие АЧХ фильтров Баттерворта и фильтров типа “К”? 6. Определите значения ФЧХ реактивного ФНЧ при частотах 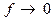и ?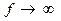

3. Анализ искажения формы периодических сигналов,

проходящих через ФНЧ

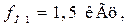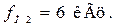Снимите осциллограммы на входе и выходе ФНЧ при двух значениях частоты повторения сигналов прямоугольной формы: и Для этого подведите курсор к изображению функционального генератора XFG1 и щелкните по нему два раза левой клавишей мыши. На открывшейся диалоговой панели нажмите кнопку (п_п_п) для установления режима генерации сигналов прямоугольной формы. Установите в строке Amplitude амплитуду прямоугольных сигналов 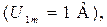а в строке Frequency установите вначале частоту повторения сигналов 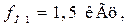что соответствует периоду повторения 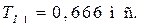Для получения длительности периодических сигналов 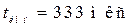установите в строке Duty Cycle величину 50%.

Для наблюдения процессов в цепи фильтра откройте экран осциллографа XSC1 двойным щелчком мыши по его изображению. Настройте осциллограф для проведения измерений. Для получения белого фона экрана осциллографа нажмите кнопку Reverse. Установите на панели управления осциллографа масштаб горизонтальной развертки (Timebase) равным 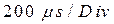и нажмите кнопку Y/ T для наблюдения изображения сигнала на экране. С помощью кнопки 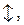расположенной в поле строки X position, установите “0” для наблюдения начала процесса в фильтре. Нажав на кнопку А C канала А (Channel A), переведите режим работы осциллографа с закрытым входом. В этом режиме на вход осциллографа пропускается только переменная составляющая сигнала. Установите цену деления канала А равной 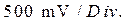С помощью кнопок 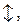расположенных в поле строки Y position, установите “0” для наблюдения осциллограммы в центре вертикальной оси. Нажмите в поле управления синхронизации Trigger кнопку Sing для запуска осциллограммы по переднему фронту входных сигналов прямоугольной формы. В случае плохой синхронизации изображения включите режим работы Pause. Для этого щелкните по клавише Simulate в командной строке и затем в открывшемся окне щелкните по клавише Pause. Далее аналогично снимите осциллограммы на входе и выходе ФНЧ при значении частоты повторения сигналов 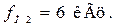Осциллограммы входного и выходного периодических сигналов зарисуйте на кальку.

Вопросы: I. Чем вызваны искажения выходных сигналов ФНЧ и при какой частоте повторения сигналов они наибольшие? 2. Попытайтесь объяснить причины изменения формы выходных сигналов. 3. Каким аналитическим выражением описывается полученный график выходного сигнала?

4. Определение частотных характеристик 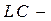фильтра верхних частот

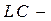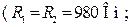
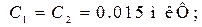
Для выполнения экспериментальных исследований фильтра верхних частот активизируйте схему, показанную на рис. 14.5. Соберите схему фильтра 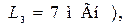изображенную на рис. 14.2, а. Установите на функциональном генераторе XFG1 амплитуду синусоидальных сигналов 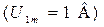в строке Amplitude. Установите в строке Frequency частоту 4 кГц. Снимите АЧХ и ФЧХ фильтра в диапазоне частот от 3 кГц до 20 кГц. При измерениях обязательно зафиксируйте граничную частоту 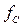по­лосы пропускания ФВЧ. Результаты измерений АЧХ и ФЧХ и результаты расчета затухания ФВЧ занесите в таблицу аналогичную табл.14.1.

Вопросы: I. Как объяснить вид АЧХ, пользуясь эквивалентной схемой реактивного ФВЧ при частотах 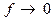и 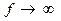? 2. Соответствует ли экспериментально снятая АЧХ характеристике фильтра Баттерворта ?

3. Определите значения ФЧХ реактивного ФВЧ при частотах 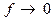и 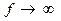? 4. Чем отличаются частотные характеристики ФНЧ и ФВЧ?

6. Анализ искажения формы периодических сигналов,

проходящих через ФВЧ

Снимите осциллограммы на входе и выходе ФНЧ при двух значениях частоты повторения сигналов прямоугольной формы: 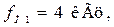и 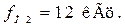Для этого на диалоговой панели функционального генератора XFG1 нажмите кнопку (п_п_п) для установления режима генерации сигналов прямоугольной формы. Установите в строке Amplitude амплитуду прямоугольных сигналов 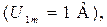а в строке Frequency установите последовательно частоты повторения сигналов: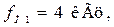 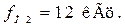Установите в строке Duty Cycle величину 50%. Осциллограммы входного и выходного периодических сигналов зарисуйте на кальку.

Вопросы: I. Чем вызваны искажения выходных сигналов ФВЧ и при какой частоте повторения сигналов они наибольшие? 2. Попытайтесь объяснить причины изменения формы выходных сигналов. 3. Укажите для какого из фильтров нижних или верхних частот искажения выходных сигналов являются большими?

7. Определение частотных характеристик реактивного полосно-пропускающего фильтра

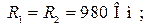
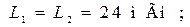
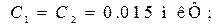
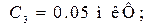
Для выполнения экспериментальных исследований реактивного полосно-пропускающего фильтра активизируйте его схему, показанную на рис. 14.5, где указаны элементы: 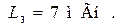Установите на функциональном генераторе XFG1 амплитуду синусоидальных сигналов 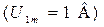в строке Amplitude. Установите на функциональном генераторе в строке Frequency частоту 4 кГц. Снимите АЧХ и ФЧХ фильтра в диапазоне частот от 3 кГц до 20 кГц. При измерениях обязательно зафиксируйте граничные частоты 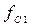и 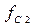по­лосы пропускания ППФ. Результаты измерений АЧХ и ФЧХ и результаты расчета затухания ФВЧ занесите в таблицу аналогичную табл. 14.1.

8. Исследование свободных процессов в цепи реактивного полосно-пропускающего фильтра

Исследование свободных процессов в цепи реактивного полосно-пропускающего фильтра произведите при воздействии периодических коротких по длительности импульсов прямоугольной формы. Для этого после активизации схемы фильтра подведите курсор к изображению функционального генератора XFG1 и щелкните по нему два раза левой клавишей мыши. На открывшейся диалоговой панели нажмите кнопку (п_п_п) для установления режима генерации сигналов прямоугольной формы. Установите в строке Amplitude амплитуду прямоугольных сигналов 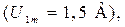а в строке Frequency установите частоту повторения сигналов 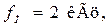что соответствует периоду повторения 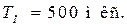Для получения длительности сигналов 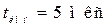установите в строке Duty Cycle величину 1%. В интервалах между короткими по длительности импульсами прямоугольной формы в цепи фильтра наблюдаются свободные процессы.

Для наблюдения свободных процессов в цепи фильтра откройте экран осциллографа XSC1 двойным щелчком мыши по его изображению. Настройте осциллограф для проведения измерений. Для получения белого фона экрана осциллографа нажмите кнопку Reverse. Установите на панели управления осциллографа масштаб горизонтальной развертки (Timebase) равным 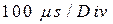и нажмите кнопку Y/ T для наблюдения изображения сигнала на экране. С помощью кнопоки 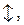расположенных в поле строки X position, установите “0” для наблюдения начала осциллограммы по горизонтальной оси. Нажав на кнопку А C канала А (Channel A), переведите режим работы осциллографа с закрытым входом. В этом режиме на вход осциллографа пропускается только переменная составляющая сигнала. Установите цену деления канала В равной 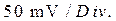С помощью кнопок 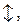расположенных в поле строки Y position, установите “0” для наблюдения осциллограммы в центре вертикальной оси. Нажмите в поле управления синхронизации Trigger кнопку Sing для запуска осциллограммы по переднему фронту входных импульсов прямоугольной формы. В случае плохой синхронизации изображения включите режим работы Pause. Для этого щелкните по клавише Simulate в командной строке и затем в открывшемся окне щелкните по клавише Pause. Осциллограмму затухающих колебаний на выходе ППФ зарисуйте на кальку.

По осциллограмме свободного процесса в цепи фильтра определите его две основные собственные частоты 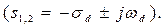С помощью мыши установите курсоры 1 и 2 на экране осциллографа на первых два соседних пика осциллограммы, временной интервал между которыми соответствует периоду собственных колебаний 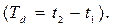На информационном поле экрана по шкале Time запишите временные интервалы 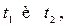а по шкале Channel В запишите амплитуды обоих пиков осциллограммы 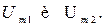Рассчитайте постоянную затухания 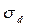и частоту затухания 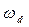по следующим формулам:

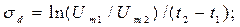
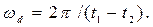
Вопросы: I. Какой порядок исследованного реактивного полосно-пропускающего фильтра? 2. Почему свободный процесс в цепи фильтра имеет затухающий характер? 3. Каким аналитическим выражением описывается полученный график свободного процесса?

14.3. Требования к отчету

Отчет должен содержать цель работы, предварительные рас­четы, все разделы экспериментального исследования и заключение. По каждому разделу необходимо включить его название, схемы исследуемых цепей, соответствующие таблицы наблюдений, вычисления, графики, осциллограммы и ответы на все вопросы. Заключение должно содержать краткие выводы по работе.