Лекция 3 Вольтамперные характеристики МОПТ
Лекция 3 Вольтамперные характеристики МОПТ
План лекции
3.1. Подпороговый размах напряжения
3.2 . Статические подпороговые токи утечки
3.3. Влияние обратного смещения на подложке
3.4 Приближение плавного канала
3.5. Плотность электронов вдоль канала при VDS >0
3.6. Простейшая модель ВАХ МОПТ
3.7. Насыщение скорости носителей в канале
3.8. Механизмы насыщения тока канала
3.9. ВАХ МОП-транзистора с учетом насыщения дрейфовой скорости
Литература
3.1. Подпороговый размах напряжения
Подпороговый ток МОПТ практически не зависит от напряжения на стоке, поскольку почти целиком состоит из диффузионной компоненты. С учетом зависимости (2.4.3)[1] концентрации носителей в канале МОПТ от поверхностного потенциала в подпороговой области ( 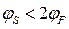 ) имеем:
) имеем:
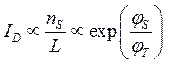 . (3.1.1)
. (3.1.1)
Как следует из формулы (2.7.4)[2], в подпороговой области 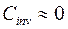 .
.
Тогда из формулы (2.8.4) имеем: 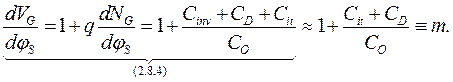 (3.1.2)
(3.1.2)
Для малых приращений 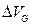 и
и 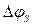 можно записать:
можно записать: 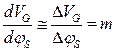 или
или
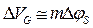 . (3.1.2а)
. (3.1.2а)
Учитывая, что напряжению VG соответствует поверхностный потенциал 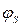 и, вспоминая, что пороговому напряжению VT и напряжению середины зоны (напряжению инверсии)
и, вспоминая, что пороговому напряжению VT и напряжению середины зоны (напряжению инверсии) 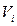 соответствуют значения поверхностных потенциалов
соответствуют значения поверхностных потенциалов 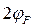 и
и 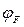 , соответственно, следуя (3.1.2а), можно записать приближенные равенства:
, соответственно, следуя (3.1.2а), можно записать приближенные равенства:
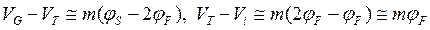 . (3.1.3)
. (3.1.3)
Используя (3.1.3) и (2.4.3), получаем плотность заряда в инверсионном слое как функцию затворного напряжения
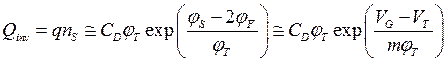 . (3.1.4)
. (3.1.4)
Это выражение справедливо только в подпороговой области, когда VG < VT , то есть при 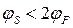 .
.
Используя (3.1.1) и (3.1.4), получаем выражение для подпорогового тока
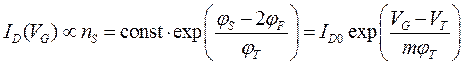 , (3.1.5)
, (3.1.5)
где 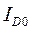 − ток стока при напряжении VG, равном пороговому напряжению.
− ток стока при напряжении VG, равном пороговому напряжению.
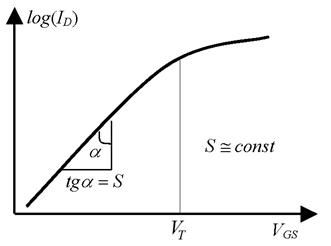
Экспериментальная зависимость логарифма тока от напряжения на затворе в подпороговой области близка к прямой линии (рис. 3.1).
|
Для характеристики наклона зависимости логарифма тока от напряжения на затворе вводится параметр – S -фактор, или подпороговый размах, который определяет насколько нужно изменить напряжение на затворе для изменения тока на декаду (изменение тока на порядок величины):
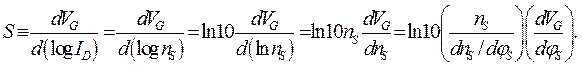 (3.1.6)
(3.1.6)
Учитывая соотношение (2.4.3), в подпороговой области ( 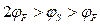 ) имеем:
) имеем:
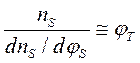 , (3.1.7)
, (3.1.7)
и, вспоминая обозначение (3.1.2) для фактора неидеальности m, имеющего смысл безразмерного отношения скоростей изменения затворного напряжения и поверхностного потенциала, получаем выражение для размаха напряжения на декаду тока:
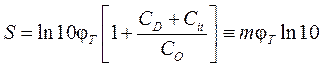 . (3.1.8)
. (3.1.8)
Эта величина характеризует возможность быстрого открывания или закрывания транзистора, а также определяет динамическое энергопотребление. Поэтому, чем меньше подпороговый размах, тем лучше. Минимально возможное значение фактора неидеальности m ~ 1, что соответствует минимально возможному (идеальному) значению размаха
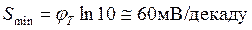 . (3.1.9)
. (3.1.9)
В коммерческих МОПТ обычно выполняется условие 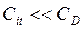 , и фактор неидеальности находится в диапазоне m ~ 1,1….1,6, что соответствует S ~ 70...100 мВ/декаду.
, и фактор неидеальности находится в диапазоне m ~ 1,1….1,6, что соответствует S ~ 70...100 мВ/декаду.
3.2 . Статические подпороговые токи утечки
Нежелательный ток между стоком и истоком в закрытом МОПТ IOFF (подпороговый ток утечки) является одной из главных проблем наноэлектронных приборов. В соответствии с (3.1.5) и (3.1.8) при 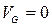 можно записать:
можно записать:
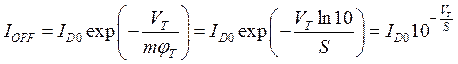 . (3.2.1)
. (3.2.1)
В современных интегральных транзисторах токи утечки лежат в пределах
10-11... 10-8 А/мкм (на единицу ширины канала).
Согласно принципам масштабирования, пороговое напряжение должно уменьшаться в той же мере, что и напряжение питания. В то же время для достижения хороших функциональных характеристик по быстродействию напряжение питания Vdd должно быть в 3-4 раза больше, чем пороговое напряжение Vt .
Здесь мы сталкиваемся с двумя противоречивыми следствиями снижения порогового напряжения. С одной стороны, низкое значение порога способствует увеличению крутизны и быстродействия (увеличивается овердрайв). С другой стороны, уменьшение Vt приводит к увеличению статических токов утечки. По этой причине пороговое напряжение нельзя делать очень маленьким. Для обеспечения минимально необходимой величины отношения токов транзистора в открытом и закрытом состоянии (динамического диапазона) в 3...4 декады ( 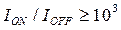 ) требуется пороговое напряжение, по меньшей мере, 0,2...0,3В.
) требуется пороговое напряжение, по меньшей мере, 0,2...0,3В.
3.3. Влияние обратного смещения на подложке
Отметим, что при обратносмещенном р-п переходе исток-подложка ( 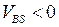 − «минус» на р-подложку, «плюс» на п-исток) даже при нулевом напряжении сток-исток (
− «минус» на р-подложку, «плюс» на п-исток) даже при нулевом напряжении сток-исток ( 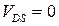 ) МДПТ не является равновесной системой, так как через переходы исток-подложка, сток-подложка и канал-подложка протекают (хотя и малые) обратные токи. В результате происходит расщепление уровня Ферми на два квазиуровня − электронный
) МДПТ не является равновесной системой, так как через переходы исток-подложка, сток-подложка и канал-подложка протекают (хотя и малые) обратные токи. В результате происходит расщепление уровня Ферми на два квазиуровня − электронный 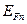 и дырочный
и дырочный 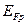 (рис. 3.2), причем в канале
(рис. 3.2), причем в канале 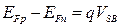 (как в обратносмещенном р-п-переходе).
(как в обратносмещенном р-п-переходе).
Как и для МДП-структуры, поверхностный потенциал в МДПТ при пороговом напряжении составляет: 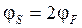 , поэтому при
, поэтому при 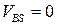 пороговая ширина ОПЗ под затвором и пороговое напряжение МДПТ определяются теми же соотношениями, что и для МДП-структуры (рис. 3.2а).
пороговая ширина ОПЗ под затвором и пороговое напряжение МДПТ определяются теми же соотношениями, что и для МДП-структуры (рис. 3.2а).

Как видно из рис. 3.2б, при 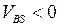 поверхностный потенциал, при котором достигается граница режима сильной инверсии (
поверхностный потенциал, при котором достигается граница режима сильной инверсии ( 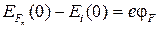 , и
, и 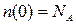 ), т.е. при пороговом напряжении, возрастает до значения
), т.е. при пороговом напряжении, возрастает до значения 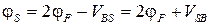 . Поэтому при
. Поэтому при 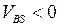 в соотношениях, определяющих пороговую ширину ОПЗ и пороговое напряжение, следует сделать замену:
в соотношениях, определяющих пороговую ширину ОПЗ и пороговое напряжение, следует сделать замену: 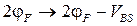 или
или 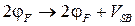 . При этом вместо (2.2.8)[3] (при
. При этом вместо (2.2.8)[3] (при 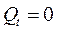 ) для п-канального МДПТ получим пороговое напряжение
) для п-канального МДПТ получим пороговое напряжение 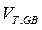 , измеренное относительно подложки (как в МДП-структуре):
, измеренное относительно подложки (как в МДП-структуре):
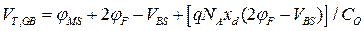 . (3.3.1а)
. (3.3.1а)
Поскольку 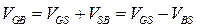 , при пороговом напряжении на затворе должно выполняться условие
, при пороговом напряжении на затворе должно выполняться условие 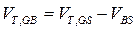 , где
, где 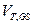 − пороговое напряжение, измеренное относительно истока:
− пороговое напряжение, измеренное относительно истока:
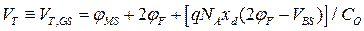 . (3.3.1б)
. (3.3.1б)
Как видно из формулы (3.3.1), обратное смещение на подложке увеличивает эффективный заряд обедненной области и соответственно увеличивает по абсолютной величине пороговое напряжение. В п-канальных транзисторах при увеличении запирающего напряжения 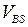 пороговое напряжение возрастает, в р-канальных – снижается (растет по абсолютной величине). Во всех случаях запирающее напряжение снижает ток стока при заданных напряжениях
пороговое напряжение возрастает, в р-канальных – снижается (растет по абсолютной величине). Во всех случаях запирающее напряжение снижает ток стока при заданных напряжениях 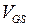 и
и 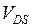 . Сравнение соотношений (2.2.8) и (3.3.1) показывает, что зависимости порогового напряжения от напряжения на подложке для п-канального (знак «+») и р-канального (знак «–») МОПТ имеют вид
. Сравнение соотношений (2.2.8) и (3.3.1) показывает, что зависимости порогового напряжения от напряжения на подложке для п-канального (знак «+») и р-канального (знак «–») МОПТ имеют вид
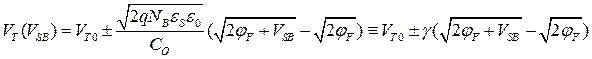 (3.3.2)
(3.3.2)
где 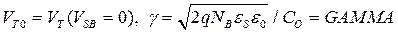 − параметр, зависящий от свойств подложки (
− параметр, зависящий от свойств подложки ( 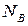 ) и свойств диэлектрика (
) и свойств диэлектрика ( 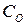 ) (в [1] называется коэффициентом влияния подложки
) (в [1] называется коэффициентом влияния подложки 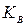 ; в нашем случае ниже будет введен другой параметр с таким названием).
; в нашем случае ниже будет введен другой параметр с таким названием).
Наклон зависимости порогового напряжения от обратного смещения определяется формулой
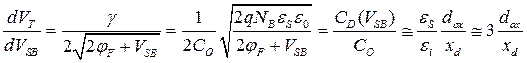 . (3.3.3)
. (3.3.3)
Как видно из формулы (3.3.3), влияние подложки возрастает с увеличением толщины подзатворного окисла и увеличением степени легирования подложки (уменьшается толщина ОПЗ).
В идеале, у каждого транзистора на чипе исток должен быть закорочен с подложкой. На практике это условие не всегда реализуется, поскольку оно ведет к усложнению конструкции и удорожанию схемы. При локальном заземлении истоков каждого из n-канальных транзисторов обратное смещение истокового перехода всегда равно нулю, и пороговое напряжение одинаково для всех n-МОПТ. Если это условие не выполняется, то возникает рассогласование пороговых напряжений разных транзисторов, что приводит к уменьшению рабочего тока, замедлению быстродействия и другим нежелательным эффектам.
3.4 Приближение плавного канала
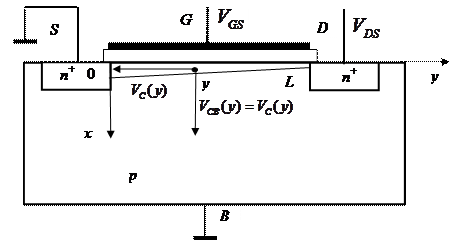
На рис.3.3 показано схематическое сечение МОП транзистора, в котором ток течет между истоком (S) и стоком (D) в канале, направленном по оси y.
Для анализа работы МОП транзистора необходимо использовать существенные приближения, главным из которых является приближение плавного канала. Приближение плавного канала состоит в том, что в каждой
|
точке канала можно записать одномерное уравнение электронейтральности для локальных значений поверхностных зарядов (концентраций)
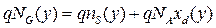 , (3.4.1)
, (3.4.1)
где 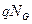 − заряд на затворе. Это приближение справедливо при выполнении формального неравенства
− заряд на затворе. Это приближение справедливо при выполнении формального неравенства
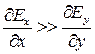 , (3.4.2)
, (3.4.2)
которое, в свою очередь, выполняется, когда электрические поля в направлении оси у существенно меньше, чем в направлении оси х.
В предыдущем разделе 3.3 предполагалось, что исток и сток находятся под одинаковым потенциалом (VS = VD). Теперь рассмотрим случай, когда исток и подложка соединены вместе и заземлены (VSB = 0), а на сток подается напряжение VDS > 0 (для определенности будем рассматривать n-МОПТ с p-подложкой и длиной канала L). Легко видеть, что поскольку исток и подложка соединены, значение потенциала канала 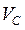 в данной точке y представляет собой локальное значение обратного смещения канала относительно и подложки, и истока в этой точке (см. рис.3.3)
в данной точке y представляет собой локальное значение обратного смещения канала относительно и подложки, и истока в этой точке (см. рис.3.3)
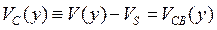 , (3.4.3)
, (3.4.3)
которое меняется от нуля в истоке до VDS на стоке:
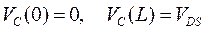 .
.
Отметим, что потенциал затвора не зависит от VDS и не меняется по всей его длине (в отличие от поверхностной плотности заряда на затворе). В этом случае выражение (2.2.5)[4], связывающее напряжение затвор-подложка и поверхностный потенциал, с учетом локального смещения подложки 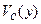 можно записать в виде
можно записать в виде
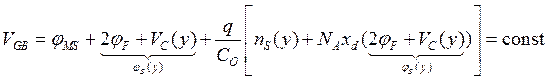 . (3.4.4)
. (3.4.4)
Анализ (3.4.4) показывает, что по мере увеличения у возрастает локальный потенциал канала V С и соответственно поверхностная плотность заряда обедненного слоя. Поскольку 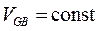 , это означает, что локальная плотность носителей в канале n S(у) уменьшается по мере приближения к стоку.
, это означает, что локальная плотность носителей в канале n S(у) уменьшается по мере приближения к стоку.
3.5. Плотность электронов вдоль канала при VDS > 0
При 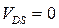 (нет тока), заземленных истоке и подложке (VSB = 0) , потенциал канала
(нет тока), заземленных истоке и подложке (VSB = 0) , потенциал канала 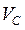 не зависит от у и равен потенциалу истока (стока):
не зависит от у и равен потенциалу истока (стока): 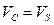 . Следовательно, разность потенциалов затвор-канал,
. Следовательно, разность потенциалов затвор-канал, 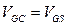 , не зависит от у, и в надпороговом режиме
, не зависит от у, и в надпороговом режиме
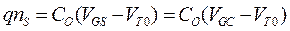 ,
,
где 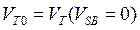 − пороговое напряжение в отсутствие смещения подложки.
− пороговое напряжение в отсутствие смещения подложки.
При 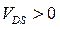 вследствие протекания тока потенциал в канале растет по направлению к стоку, и появляется зависимость
вследствие протекания тока потенциал в канале растет по направлению к стоку, и появляется зависимость 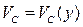 . В результате этого по направлению к стоку, во-первых, изменяется (уменьшается) разность потенциалов затвор-канал
. В результате этого по направлению к стоку, во-первых, изменяется (уменьшается) разность потенциалов затвор-канал 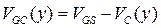 , во-вторых, изменяется (увеличивается) напряжение канал-подложка
, во-вторых, изменяется (увеличивается) напряжение канал-подложка 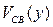 . Поскольку
. Поскольку 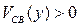 , это эквивалентно подаче локального обратного смещения
, это эквивалентно подаче локального обратного смещения 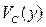 на подложку (см. рис.3.3), и пороговое напряжение начинает локально зависеть от напряжения
на подложку (см. рис.3.3), и пороговое напряжение начинает локально зависеть от напряжения 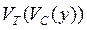 .
.
Это позволяет записать плотность электронов в каждой точке канала в виде
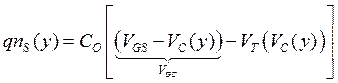 .
.
Поскольку 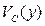 играет роль локального смещения на подложку, можно воспользоваться формулой (3.3.3)[5] и записать (разложение в ряд Тейлора):
играет роль локального смещения на подложку, можно воспользоваться формулой (3.3.3)[5] и записать (разложение в ряд Тейлора):
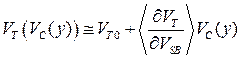 ,
,
где 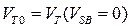 . Угловые скобки означают, что берется некоторое среднее значение производной на длине канала. Тогда
. Угловые скобки означают, что берется некоторое среднее значение производной на длине канала. Тогда
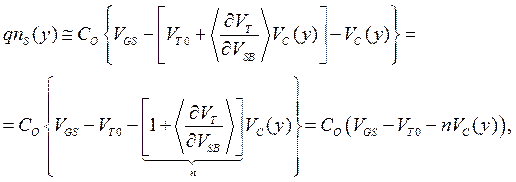 (3.5.1)
(3.5.1)
где введен безразмерный параметр