Лекция (к занятиям № 1-3)

Дата: 2025-06-02; Просмотры: 7
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Тема. Развитие понятия о числах. Комплексные числа и действия над ними. Алгебраическая и тригонометрическая форма комплексного числа.

 

План.

1. Введение в теорию комплексных чисел.

2. Арифметические операции над комплексными числами.

3. Алгебраическая форма комплексного числа.

4. Геометрическое изображение комплексных чисел.

 

1. Введение в теорию комплексных чисел

Понятие о комплексном числе появилось в середине 16 в. Математиков того времени заинтересовал вопрос, получения формул выражающих корни кубического уравнения через его коэффициенты.

В 1545г. была издана книга «Великое искусство, или об алгебраических преобразованиях», в которой Дж.Кардано (1501-1576) опубликовал формулу корней кубического уравнения, открытую его современниками С. дель Ферро(1465-1526) и Н. Тартальей(1500-1557). Обнаружилось, что в случае, когда кубическое уравнение имеет три действительных корня, в формуле Кардана появляются квадратные корни из отрицательного числа. Такие числа называются мнимыми числами.

Мнимые числа стали широко использовать при решении уравнений. На рубеже 18 и 19вв. К.Ф. Гаусс назвал мнимые числа «Комплексными числами». Он дал им геометрическую интерпретацию и доказал, что каждый многочлен, степень которого не меньше единицы, имеет хотя бы один корень, действительный или комплексный.

В настоящее время комплексные числа широко применяются в математике, физике и технике; их применение часто упрощает решение задач.

1. Понятие мнимой единицы.

Предположим, что существует такое число, квадрат которого равен - 1. Обозначим это число буквой i, тогда справедливо равенство (1):

Число i будем называть мнимой единицей, а равенство (1) будем считать определением мнимой единицы.

2. Степень мнимой единицы.

Рассмотрим степени мнимой единицы:

i ;
i2 = – 1;
i3 = i2*i = (– 1)i = – i;
i4 = i3*i = – i*i = – i2 = – (– 1) = 1;
i5 = i4*i = 1*i = i;
i6 = i5*i = i*i = i2 = – 1;
i7 = i6*i = (– 1)*i = – i;
i8 = i7*i = – i*i = 1;
Таким образом ,

- если показатель степени числа i делится на 4, то значение степени равно 1;

- если при делении показателя степени на 4 в остатке получается 1, то значение степени равно i ;

- если при делении показателя степени на 4 получается остаток 2, то значение степени равно – 1;

- если при делении на 4 остаток равен 3, то значение степени равно – i.

Пользуясь этим, можно вычислять любую степень числа i.

Например:

а) і28 = 1, т.к. 28=4*7 (нет остатка)

б) і33 = і, т.к. 33=4*8+1

в) і135 = - і, т.к. 135=4*33+3

 

Задания для самостоятельной работы №1.

Вычислите:

1. i66; i143; i216; i137.
2. i43 + i48 + i44 + i45.
3. (i36 + i17)i23.
4. (i133 + i115 + i200 + i142)(i17 + i36).
5. i145 + i147 + i264 + i345 + i117.
6. (i13 + i14 + i15)i32.
7. (i64 + i17 + i13 + i82)(i72 – i34).

 

3. Основные определения и свойства.

Определение 1. Комплексным числом называется выражение вида a+bi , где a и b –действительные числа, а i-мнимая единица. Множество комплексных чисел обозначается через C.

Возможны случаи, когда a и b могут быть равные нулю.

- если a = 0, то комплексное число bi называют мнимым;

- если b = 0, то комплексное число a+bi = a и называется действительным;

- если a =0 и b=0,то комплексное число a+bi=0.

Определение 2. Комплексные числа z = a + b і и z = c + d і называются равными, если a =c и b=d.

Например:

a) Найти x и y из равенства 3y+5xi=15-7i

Решение:

Согласно условию равенства комплексных чисел имеем 3y=15; 5x=-7.Отсюда

б) Найти x и y из равенства(2х+3у) + (х-у)I =7+6i

Решение: Согласно условию равенства комплексных чисел имеем

2х+3у=7

х-у=6

Решая систему уравнений получаем: х=5,у=-1

 

Задания для самостоятельной работы №2.

8–13. Найдите значения x и y из равенств:

8. 7x + 5i = 1 – 10iy. 9. (2x + y) – i = 5 + (y – x)i.
10. x + (3x – y)i = 2 – i. 11. (1 + 2i)x + (3 – 5i)y = 1 – 3i.
12. (2 – i)x + (1 + i)y = 5 – i. 13. (3i – 1) x + (2 – 3i)y = 2 – 3i.

 

Определение 3. Суммой комплексных чисел z = a + b і и z = c + d і называется комплексное число вида (a+c)+(b+d)i

Например:

Найти сумму комплексных чисел z1 = 2- і и z2= -1+3і

Решение: z1 + z2 = (2-1) + (-1+3)і = 2+2і;

Определение 4. Произведением комплексных чисел z = a + b і и z = c + d і называется комплексное число вида (ac - bd) + (ad + bc)i

Например:

Найти произведение комплексных чисел z1 = 2- 3і и z2= -4+3і

Решение: z1 z2= (2- 3і) (-4+3і) = 2(-4)+ (-3і)(-4)+2*3і+(-3і)*3і= -8+12і+6і+9=1+18і;

З амечание . При выполнении умножения можно использовать формулы сокращенного умножения:

Например

а) (2 + 3i)2 = 4 + 2*2*3i + 9i2 = 4 + 12i – 9 = – 5 + 12i;

б) (3 – 5i)2 = 9 – 2*3*5i + 25i2 = 9 – 30i – 25 = – 16 – 30i;

в) (5 + 3i)(5 – 3i) = 52 – (3i)2 = 25 – 9i2 = 25 + 9 = 34;

г) (1 + i)(1 – i) = 12 – i2 = 1 + 1 = 2

 

Операции суммы и произведения комплексных чисел обладают следующими свойствами:

I. Свойства суммы:

- коммутативности: z1 + z2= z2 + z1;

- ассоциативности: (z1 + z2) + z3 = z1 + (z2 + z3);

II. Свойства произведения:

- коммутативности: z1 * z2= z2 * z1;

- ассоциативности: (z1* z2) * z3 = z1 * (z2 * z3);

III. Свойство дистрибутивности: z1 *( z2 + z3) = z1 * z2 + z1*z3);

Определение 5. Алгебраической формой записи комплексного числа называется запись вида z = a+bi, где i-мнимая единица.

Сложение и умножение комплексных чисел, заданных в алгебраической форме, осуществляется по обычным правилам алгебры с учетом равенства

i 2 = – 1.

Определение 6: Разностью комплексных чисел z = a + b і и z = c + d і называется число z = x + yi, которое удовлетворяет равенству (c+di)+(x+yi)=a+bi

Например

Вычислите: (2+6i)−(7+11i)=(2-7)+(6i-11i)= -5-5i

Задания для самостоятельной работы №3.

Вычислите:

14. (3 + 5i) + (7 – 2i). 15. (6 + 2i) + (5 + 3i)

16. (– 2 + 3i) + (7 – 2i). 17. (5 – 4i) + (6 + 2i).
18. (3 – 2i) + (5 + i). 19. (4 + 2i) + (– 3 + 2i).
20. (– 5 + 2i) + (5 + 2i). 21. (– 3 – 5i) + (7 – 2i)

22. (2 + 3i)(5 – 7i). 23. (6 + 4i)(5 + 2i).
24. (3 – 2i)(7 – i). 25. (– 2 + 3i)(3 + 5i).
26. (1 –i)(1 + i). 27. (3 + 2i)(1 + i).
28. (6 + 4i)*3i. 29. (2 – 3i)(– 5i).

30. (3 + 5i)2. 31. (2 – 7i)2

32. (6 + i)2. 33. (1 – 5i)2.

34. (3 + 2i)3. 35. (3 – 2i)3.
36. (4 + 2i)3. 37. (5 – i)3.

38. (3 + 2i)(3 – 2i). 39. (5 + i)(5 – i).
40. (1 – 3i)(1 + 3i). 41. (7 – 6i)(7 + 6i).
42. (a + bi)(a – bi). 43. (m – ni)(m + ni).

 

Пример. Даны комплексные числа z1 = (2,7), z2 = (3,-1). Найти их сумму, разницу, произведение, частное и вторую степень z1.

 

1. z1 + z2 = (2,7) + (3,-1) = (5,6). 2. z1 - z2 = (2,7) - (3,-1) = (-1,8).

 

3. z1z2 = (2,7) × (3,-1) = (13,19). 4. z1 : z2 = (2,7) : (3,-1) = (-0.1,2.3).

5. z2 = (2,7) × (2,7) = (-45,28).

Определение 6. Комплексные числа а + bi й а – bi называются взаимно сопряженными комплексными числами.

Их сумма и произведение - вещественные числа:

(а + bi) +(а - bi) = 2а

(а + bi)(а - bi) = а2 + b2.

Пример. Уравнение х2 – 4 х + 13 = 0 имеет корень х1 = 2 + 3i, х2 = 2 - 3i Заметим, что уравнение х2 + 1 = 0 имеет два решения х1 = i, х2 = -i.

Алгебраическая форма комплексного числа позволяет производить алгебраические действия по следующему правилу: нужно рассматривать выражение вида а+bi как многочлен и делать над многочленами привычные алгебраические действия с последующей заметкой i2 на -1 Отдельно

(а + bi)(а - bi) = а2 – аbi + аbi – b2 i2 = а2 + b2,

и 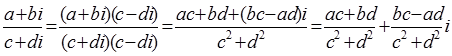. (9)

 

4. Геометрическое изображение комплексных чисел.

Для изображения любого комплексного числа (a,b) , которое не является вещественным, очевидно нужна точка плоскости. Естественно комплексному числу (а,b) сопоставить точку плоскости (х, у) с координатами х=а, у= b, то есть точку М (а,b) (Рис.1).

 

 

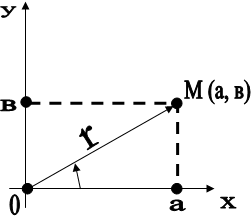
Мы установили взаимно однозначное соответствие между множеством точек плоскости хОу и множеством комплексных чисел:

z = (х,у) = х + уi.

 

Плоскость хОу, на которой изображаются комплексные числа, называют комплексной плоскостью z (Рис.2).

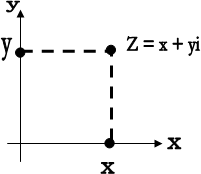Точку М(а,b), что изображает комплексное число а+bi, отождествляют с самим числом, говоря, что последнее

 


расположено в точке М.

 

 

Можно также

говорить о векторе ОМ, которому соответствует комплексное число (а,b) = а + b Рис.2.

Комплексные числа вида (0,b) = bi называют чисто мнимыми числами, а число i – мнимым единицей. Числа a и b называют соответственно вещественной и мнимой частями комплексного числа z = a + bi.

В соответствии с этим координатные оси комплексной плоскости называют вещественной и мнимым осям: на вещественной оси расположены вещественные числа, а на мнимой оси – чисто мнимые. Взаимно сопряженные комплексные числа а + bi и а - bi расположены симметрично относительно вещественной оси (Рис. 3)

 

y

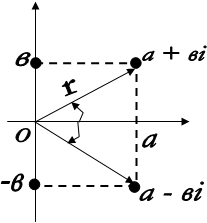
Для комплексных чисел вводятся понятия модуля аргумента, которые впоєне характеризуют комплексное число и положение его точки, изображенное на комплексной плоскости.

- φ x

 

Рис. 3.

Определение 7. Модулем комплексного числа (a,b) = a + bi = z (Рис. 1) называется вещественное число .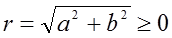

Это число равно расстоянию от начала координат до точки М (A,b), изображающего комплексное число, или длине вектора ОМ. Имеют место соотношения:

| a | = | Rez | < r , | b | = | Imz | < r, | z | ≤ | a | + | b |.

Определение 8. Аргументом комплексного числа, отличного от нуля, называется угол φ, на который нужно повернуть положительную часть вещественной оси до совпадения с вектором ОМ. Этот угол положительный, если поворот идет против часовой стрелки.

Пример. Аргументы чисел 1 + i и 1-i равны соответственно p/4 и -p/4считается, что аргумент положительного вещественного числа равен нулю, а аргумент отрицательного вещественного числа равен π.

Аргумент чисто мнимого числа bi равен p /2 при b > 0 и -- p /2, при b < 0.

Два комплексных числа равны, если их модули равны, а аргументы отличаются на число, кратное 2π.

Аргумент φ комплексного числа z = a + ib записывается так: φ=Argz, или φ=Arg(a+ib).

Для числа z = 0 аргумент не определяется.

Для фиксированного числа z = 0 аргумент определяется неоднозначно: если φ – одно из значений аргумента числа z, то углы φ + 2π, доÎZ, тоже являются значениями аргумента того же числа z. Таким образом, для каждого числа z имеет бесконечное множество значений аргумента.

Главное значение аргумента принадлежит промежутку- p < argz £ p.

Из определения тригонометрических функций следует, что если j=Arg(a+bi),, то имеют место равенства

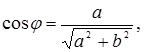
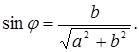(10)

 

Все значения аргумента комплексного числа z=a+ib ¹ 0 можно находить так:

1. Определить в какой четверти находится точка z (используя геометрическую интерпретацию числа z=а + bi).

2. В этой четверти найдите угол φ, решив одно из уравнений (10) или уравнения tg φ =b/a.

3. Найти все значения аргумента числа z по формуле

Argz= j+2pk, kÎZ.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Как определяется алгебраическая форма комплексного числа?

2. Можно ли установить взаимно однозначное соответствие между множеством комплексных чисел и точками некоторой плоскости?

3. Каково соотношение между вещественными и комплексными числами?

4. Почему комплексные корни квадратного уравнения (с вещественными коэффициентами) обязательно являются сопряженными комплексными числами?

5. Или комплексное число определяется однозначно своим аргументом и модулем?

6. Может ли аргумент (модуль) комплексного числа быть выражен вещественным отрицательным числом?

 

ОСНОВНЫЕ ТЕРМИНЫ И ПОНЯТИЯ.

 

Комплексное число

Алгебраическая форма комплексного числа

Чисто мнимые числа

Мнимая единица

Положительное вещественное число

Вещественная и мнимая оси

Взаимно сопряженные комплексные числа

Тригонометрическая форма комплексного числа

Модуль комплексного числа

Аргумент комплексного числа

 

ЛИТЕРАТУРА.

 

1. “ Высшая математика для экономистов”, ред. Н.Ш. Кремера Н. : ЮНИТИ, 1998, с. 438 - 444.

2. “Курс математики для техникумов, ч. 1”, ред. Н. М. Матвеева. - М.: Наука, 1976, с. 22 (29, 337 - 342.

3. В.В. Пак, Ю.Л. Носенко “Высшая математика”, Д.: Сталкер, 1997, с. 170-173.