Тема: обчислення множинних і часткових коефіцієнтів кореляції
робота №5
Тема: обчислення множинних і часткових коефіцієнтів кореляції
Мета: надбання навичок обчислення множинних і часткових коефіцієнтів кореляції.
1. Основні теоретичні положення
Багатофакторна економетрична модель містить одну результативну ознаку (у) та m факторних ознак (х1, х2, …, хm). Між кожною парою ознак існує кореляційний зв'язок, який можна вимірити кількісно парним коефіцієнтом кореляції
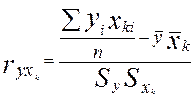 ,
, 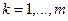 ;
;
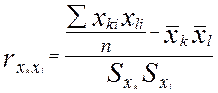 ,
, 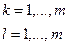 .
.
З цих коефіцієнтів кореляції можна скласти кореляційну матрицю 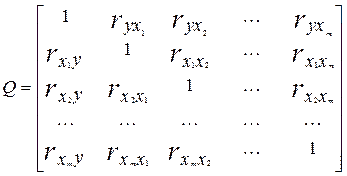 .
.
Під час побудови цієї матриці керуються таким правилом:
- ознаки нумерують в такому порядку:
| у | х1 | х2 | … | хm , |
| 1 | 2 | 3 | … | m+1 ; |
Таким чином, i-ому рядку (стовпцю) відповідає (i–1)-а факторна ознака хi-1;
- на перетинанні i-ого рядка і j-го стовпця розташовують коефіцієнт кореляції між (i-1)-ою і (j-1)-ою ознаками.
Коефіцієнтам кореляції притаманні дві основні властивості:
1) коефіцієнт кореляції ознаки із самою собою дорівнює 1
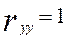 ;
; 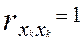 .
.
Дійсно,
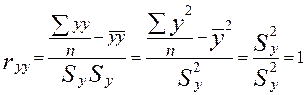 .
.
Аналогічно для 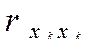 ;
;
2) значення коефіцієнта кореляції не залежить від порядку проходження ознак 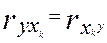 ;
; 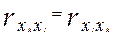 .
.
Ця властивість випливає з формули коефіцієнта кореляції, у якій зміна порядку проходження ознак призводить до перестановки співмножників, від чого добуток не змінюється.
З цих двох властивостей коефіцієнтів кореляції випливають такі властивості кореляційної матриці:
1) елементи головної діагоналі кореляційної матриці дорівнюють 1;
2) матриця симетрична щодо головної діагоналі, тобто не змінюється при транспонуванні.
Таким чином, в остаточному вигляді кореляційну матрицю можна записати так:
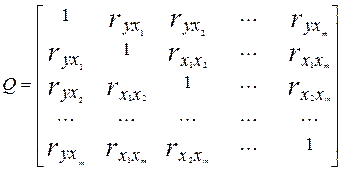 .
.
Множинний коефіцієнт детермінації визначає частку варіації результативної ознаки (у), що пояснюється варіацією всієї сукупності факторних ознак (х1, х2, …, хm). Обчислюють множинний коефіцієнт детермінації за формулою
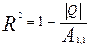 , (1)
, (1)
де 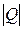 – визначник кореляційної матриці;
– визначник кореляційної матриці;
А1,1 – алгебраїчне доповнення до елемента матриці, що знаходиться на перетинанні 1-ого рядка і 1-го стовпця.
Алгебраїчне доповнення Ai,j обчислюється за таким принципом
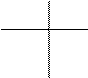
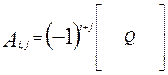 i ,
i ,
j
тобто алгебраїчне доповнення Ai,j обчислюється з визначника кореляційної матриці, у якій викреслені i-ий рядок і j-ий стовпець.
Множинний коефіцієнт кореляції R вимірює тісноту кореляційного зв'язку результативної ознаки (у) із усією сукупністю факторних ознак (х1, х2, …, хm)
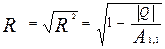 . (2)
. (2)
При обчисленні парних коефіцієнтів кореляції 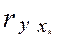 передбачається, що вся зміна у викликана впливом лише фактора xk . У дійсності це не так, оскільки на зміну у крім xk впливають й інші ознаки, тому істинну (справжню) тісноту кореляційного зв'язку між у і кожною з факторних ознак (х1, х2, …, хm) у випадку множинної кореляції вимірюють частковими коефіцієнтами кореляції
передбачається, що вся зміна у викликана впливом лише фактора xk . У дійсності це не так, оскільки на зміну у крім xk впливають й інші ознаки, тому істинну (справжню) тісноту кореляційного зв'язку між у і кожною з факторних ознак (х1, х2, …, хm) у випадку множинної кореляції вимірюють частковими коефіцієнтами кореляції
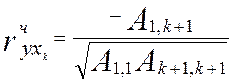 . (3)
. (3)
При обчислення часткових коефіцієнтів кореляції за допомогою Microsoft Excel можна використовувати і метод, що заснований на обчисленні зворотної матриці. Дійсно, якщо
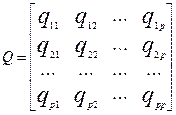 ,
,

де p=m+1, то зворотна матриця 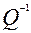 буде дорівнювати
буде дорівнювати
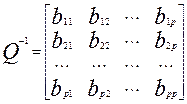 ,
,
де 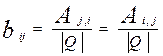 . Остання рівність пояснюється симетричністю кореляційної матриці.
. Остання рівність пояснюється симетричністю кореляційної матриці.
Тоді частковий коефіцієнт кореляції
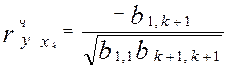 , (4)
, (4)
що еквівалентно формулі (2), тому що
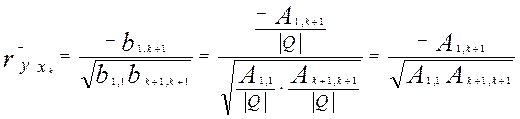 .
.
Таким чином, існує два способи обчислення часткових коефіцієнтів кореляції:
1. Обчислення за формулою (3) на основі алгебраїчних доповнень.
2. Обчислення матриці, зворотної до кореляційної матриці, і обчислення за формулою (4).
2. Завдання
Зібрано статистичні дані про попит на одяг, а також про ціни одягу, взуття, побутових товарів і дохід за період 10 місяців (табл. 1).
Таблиця 1
Попит на одяг, ціна одягу, ціна взуття, ціна побутових товарів і дохід
| Час, t | Ціна одягу, х1, грн. | Ціна взуття, х2, грн. | Ціна побутових товарів, х3, грн. | Доход, х4, грн./міс. | Попит на одяг, у, шт./рік |
| 1 | 130 | 70 | 10 | 220 | 1,8·(1+0,1N) |
| 2 | 110 | 80 | 12 | 210 | 1,6·(1+0,1N) |
| 3 | 90 | 95 | 15 | 200 | 0,5·(1+0,1N) |
| 4 | 130 | 75 | 10 | 230 | 1,9·(1+0,1N) |
| 5 | 120 | 60 | 13 | 240 | 2,3·(1+0,1N) |
| 6 | 105 | 70 | 16 | 270 | 2,6·(1+0,1N) |
| 7 | 125 | 65 | 19 | 260 | 1,9·(1+0,1N) |
| 8 | 140 | 90 | 20 | 300 | 1,6·(1+0,1N) |
| 9 | 130 | 100 | 18 | 290 | 1,7·(1+0,1N) |
| 10 | 150 | 80 | 17 | 330 | 2,7·(1+0,1N) |
Необхідно установити ступінь сукупного впливу цін і доходу на попит (обчислити множинний коефіцієнт кореляції і множинний коефіцієнт детермінації, визначити значущість множинного коефіцієнта кореляції), а також ступінь впливу на попит на одяг кожної факторної ознаки окремо (обчислити часткові коефіцієнти кореляції двома способами).
Проаналізувати отримані результати і зробити висновки.
3. Приклад обчислення множинних і часткових коефіцієнтів кореляції
Для сільськогосподарського регіону обчислюється виробнича функція за даними за 10 років (n=10). Факторні ознаки моделі х1 – основні засоби, х2 – трудові ресурси, х3 – земельні ресурси; результативна ознака у – валова продукція регіону.
За звітними даними розраховані парні коефіцієнти кореляції 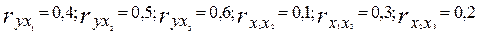 .
.
Необхідно установити ступінь сукупного впливу перерахованих факторних ознак на величину валової продукції сільськогосподарського регіону (обчислити множинний коефіцієнт кореляції і детермінації, визначити значущість множинного коефіцієнта кореляції), а також ступінь впливу на результативну ознаку кожної з факторних ознак окремо (обчислити часткові коефіцієнти кореляції).
5.1. Обчислюємо множинний коефіцієнт детермінації R2, множинний коефіцієнт кореляції R та оцінимо його значущість:
- за вихідними даними складемо кореляційну матрицю
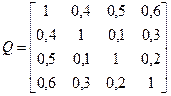 ;
;
- за допомогою убудованої функції МОПРЕД(…) (категорія «Математичні» майстра функцій) знайдемо визначник кореляційної матриці 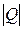 = 0,3869;
= 0,3869;
- за допомогою убудованої функції МОПРЕД(…) (категорія «Математичні» майстра функцій) знайдемо алгебраїчне доповнення А1,1 = 0,872;
- розрахуємо множинний коефіцієнт детермінації
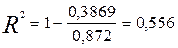 .
.
- обчислимо множинний коефіцієнт кореляції 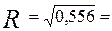 0,746;
0,746;
- обчислимо помилку множинного коефіцієнта кореляції
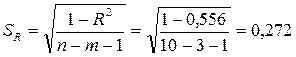 ;
;
- обчислимо коефіцієнт надійності множинного коефіцієнта кореляції
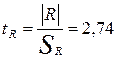 .
.
Висновок: 55,6% варіації валової продукції сільськогосподарського регіону обумовлено варіацією ресурсів, що враховані в даній моделі, а 44,4% – впливом неврахованих факторів. Щільність кореляційного зв'язку сильна, тому що R>0,7. tтабл = 2,45 (при 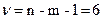 ). Розрахункове значення статистики Ст’юдента більше табличного, тому множинний коефіцієнт кореляції R є значущим.
). Розрахункове значення статистики Ст’юдента більше табличного, тому множинний коефіцієнт кореляції R є значущим.
5.2. Розрахуємо часткові коефіцієнти кореляції двома способами.
3.2.1. Розрахуємо часткові коефіцієнти кореляції першим способом:
- за допомогою убудованої функції МОПРЕД(…) (категорія «Математичні» майстра функцій) знаходимо алгебраїчні доповнення:
А1,2 = -0,196; А1,3 = -0,337; А1,4 = -0,397; А2,2 = 0,47; А3,3 = 0,534; А4,4 = 0,62.
- розрахуємо часткові коефіцієнти кореляції (формула 3):
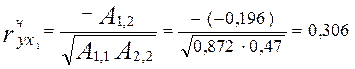 ;
;
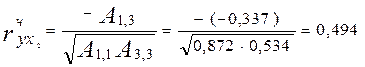 ;
;
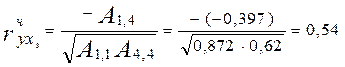 .
.
3.2.2. Розрахуємо часткові коефіцієнти кореляції другим способом:
- за допомогою убудованої функції МОБР(…) (категорія «Математичні» майстра функцій) обчислюємо матрицю, зворотну до кореляційної матриці
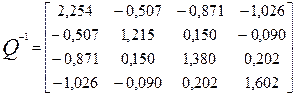 ;
;
- обчислимо часткові коефіцієнти кореляції (формула 4):
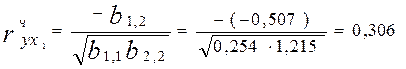 ;
;
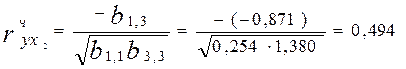 ;
;
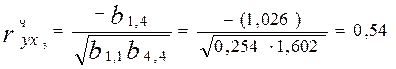 .
.
Висновок: часткові коефіцієнти кореляції в даному прикладі виявились менше парних коефіцієнтів кореляції, тому що враховують вплив на результативну ознаку (валову продукцію) тільки одного з ресурсів. Тобто дійсна сила взаємозв’зку між валовою продукцією та ресурсами дещо менша та відповідає середньому ступеню зв’язку.
Список Рекомендованої літератури
1. Лук’яненко I.Г., Краснікова Л.І. Економетрика / Підручник. – К.: Товариство «Знання», КОО, 1998. – 494 с.
2. Наконечний С.І. та ін. Економетрія: Підручник / Вид. 2-ге, допов. та перероб. – К.: КНЕУ, 2000. – 296 с.
3. Экономико-математические методы и модели в планировании и управлении: Учебник / В.Н. Кухарев, В.И. Салли, А.М. Эрперт – К.: Выща шк., 1991. – 302 с.
4. статистика: Учеб. пособие для экон. спец. вузов – М.: Высш. шк., 1991 – 399 с.
5. Джонстон Дж. Эконометрические методы / Пер. с англ. и предисл. А.А. Рывкина. – М.: Статистика, 1980. – 444 с.
Укладачі
Трифонова Олена Василівна
Олійник Світлана Павлівна
Шликова Валентина Михайлівна
Методичні вказівки
до лабораторних робіт з дисципліни «Економетрія»
для студентів напряму 6.030601 Менеджмент
Редакційно-видавничий комплекс
Редактор
Підписано до друку . Формат 30х42/4.
Папір Сaptain. Ризографія. Обліково-видавн. арк. .
Умовн. друк. арк. . Тираж прим. Зам. №
ДВНЗ «НГУ»
| |
49005, м. Дніпропетровськ, К. Маркса, 19.








