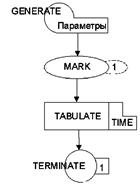
3 Блок–схема модели
Блок–схема модели приведена на рис.1.3.
Пример моделирования случайной величины с дискретным равномерным распределением
|
|
Программа моделирования на GPSS приведена на рис.1.4.
| Рис. 1.3 |
| SIMULATE | |
| TIME | EQU 1 |
| GENERATE 20,15 | |
| MARK 1 | |
| TABULATE TIME | |
| TERMINATE 1 | |
| TIME | TABLE P$1–,5,5,10 |
| START 251 | |
| END |
Рис.1.4
4.Особенности работы в среде GPSS/PC
Папка GPSS с системными файлами копируется на какой–либо локальный логический диск.
Файл с исходным текстом модели должен иметь расширение .gps и располагаться в одной папке с системными файлами.
Прогон модели осуществляется из командной строки по команде GPSS.bat имя файла.gps .
Выход из среды GPSS/PC производится по команде QUIT.
Листинг результатов моделирования формируется автоматически в файле с тем же именем, что и для файла с исходным текстом модели, но расширением .lst.
Переход в режим HELP производится в среде GPSS/PC по команде ? или HELP. По команде NEXT в командной строке среды GPSS/PC происходит формирование следующего отчета по результатам моделирования (при нескольких картах START или использовании счетчика снимков в карте START).
Вся необходимая информация по имитационному моделированию содержится в соответствующих текстовых файлах.
Задание
Провести моделирование случайной величины средствами GPSS и языка программирования.
Содержание отчета
1. Задание.
2. Метод построения моделей на GPSS и алгоритмическом языке.
3. Q–схема математической модели.
4. Таблица определений GPSS–модели.
5. Блок–схема GPSS–модели.
6. Листинги моделей.
7. Гистограммы, полученные по результатам моделирования; mx, σx.
8. Выводы по выполненной работе.
Варианты заданий
Варианты заданий, параметры и значения случайной величины приведены в следующих таблицах:
9
Таблица 1.3
| Вари ант | Вид распределения | Параметры | Количество значений | |||||||||
| a | b | l | табл. | |||||||||
| 1. | Равномерное дискретное | 20 | 30 |
|
| 250 | ||||||
| 2. | Равномерное непрерывное | 1 | 10 |
|
| 250 | ||||||
| 3. | Неравномерное дискретное |
|
|
| табл. 1.4 | 250 | ||||||
| 4. | Экспоненциальное |
|
| 0.1 |
| 250 | ||||||
| 5. | Эрланга 2–го порядка |
|
| 0.1 |
| 200 | ||||||
| 6. | Неравномерное дискретное |
|
|
| табл. 1.5 | 200 | ||||||
| 7. | Экспоненциальное |
|
| 0.025 |
| 200 | ||||||
| 8. | Равномерное непрерывное | 13 | 20 |
|
| 200 | ||||||
| 9. | Равномерное дискретное | 30 | 40 |
|
| 200 | ||||||
| 10. | Экспоненциальное |
|
| 0.05 |
| 250 | ||||||
Таблица 1.4 Таблица 1.5
| Значения случ/величины | Относительная частота | Значения случайной величины | Относительная частота |
| 2 | 0,1 | 5 | 0,05 |
| 3 | 0,3 | 6 | 0,12 |
| 4 | 0,4 | 7 | 0,28 |
| 5 | 0,2 | 8 | 0,3 |
| 9 | 0,18 | ||
| 10 | 0,07 |