Экспоненциальное распределение

Дата: 2025-06-02; Просмотры: 16

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Функция плотности распределения имеет следующий вид: l

f(x)=le^–lx , x > 0; f(x) =0, x < 0 ;

m_x = 1/l ; s_x² = 1/ l²

В GPSS для моделирования экспоненциально распределенной случайной величины при среднем значении, равном 1, используется следующая функция:

XPDIS FUNCTION RN$1,C24

0,0/.1,.104/.2,.222/.3,.355/.4,.509/.5,.69/.6,.915/.7,1.2/.75,1.38 .8,1.6/.84,1.83/.88,2.12/.9,2.3/.92,2.52/.94,2.81/.95,2.99 .96,3.2/.97,3.5/.98,3.9/.99,4.6/.995,5.3/.998,6.2/.999,7/.9998,8

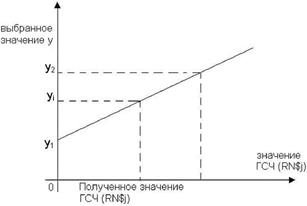
Рис. 1.2

Если среднее значение случайной величины отлично от 1, то в блоках GENERATE или ADVANCE ссылка на функцию XPDIS задается так: GENERATE среднее значение, FN$XPDIS.

Моделирование экспоненциально распределенной случайной величины средствами языков программирования аналогично предыдущему распределению.

Распределение Эрланга

Функция плотности распределения имеет следующий вид:

f(x)=l 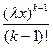e^–lx , x > 0; f(x) =0, x < 0

где k – порядок распределения Эрланга;

λ – интенсивность потока Эрланга; m_x = k/λ; σ_x² = k/λ².

Примером моделирования потока Эрланга 2–го порядка при l = 0.1 в GPSS является следующая функция:

ERLAN FUNCTION RN $1, C 24

0,0/ .0176, 2/ .0616, .4/ .1219, .6/ .1913, .8 / .2642, 1 .3374, 1.2/ .4082, 1.4/ .4751, 1.6/ .5372, 1.8/ .5941,2 .6454, 2.2/ .6915, 2.4/ .7326, 2.6/ .7689, 2.8/ .8008,3 .8641, 3.5/ .9084, 4/ .9596, 5 .9826, 6/ .9927, 7/ .997,8 .9988, 9.0/ .9995, 10

Ссылка на функцию имеет следующий вид:

GENERATE 1/λ , FN $ ERLAN.

В случае моделирования случайной величины с распределением Эрланга средствами языка программирования используют соотношение:

k

y_i = ∑ x_j,

j=1

где y_i – случайная величина с распределением Эрланга k–го порядка;

x_j – случайная величина, распределенная по экспоненциальному за–кону с параметром λ.

2 Метод построения модели

При моделировании случайных величин на GPSS в качестве значения случай–ной величины берется временной интервал между моментами поступления транзактов в модель. В случае моделирования на алгоритмическом языке для получения значения случайной величины необходимо обращение к ГСЧ и вычисление выражения, полученного преобразованием (2).