Равномерное дискретное распределение.
В GPSS данное распределение задается в блоках GENERATE или ADVANCE операндами A и B, где A – среднее значение случайной величины, B – отклонение от среднего.
Например, GENERATE 16,4 задает интервал поступления транзактов в мо–дель как выборку из девяти значений:
12, 13, 14, 15, 16, 17, 18, 19, 20
Для получения данного распределения средствами языков программирования следует использовать формулу:
yi = [( A – B ) + ui (2 B + 1)] , (1)
где yi – целая часть выражения, случайная величина, равномерно распределен–ная в интервале [(A – B); (A +B)]; ui – случайная величина, равномерно распределенная в интервале [0;0.999999].
Неравномерное дискретное распределение.
Случайная величина задается своими значениями yi, i = 1, 2, ... , n и соответст–вующими им вероятностями (или относительными частотами) Pi.
В GPSS закон распределения случайной величины задается картой FUNCTION (табл.1.1)
Таблица 1.1
| 1 ... 7 | 8 ... 18 | 19 ... |
| имя | FUNCTION | RN$j , Dn |
| z1, y1 / z2, | y2 / . . . / zn, yn |
где имя – числовое (целое положительное число) или символьное имя; j = 1, 2, ..., 8;
n – число значений случайной величины yi ; i zi – значение суммарной частоты, причем zi = ∑ Pj , i = 1,...,n;
|
|
z1 < z2 < z3 <…< zn . j=1
Ссылка на функцию имеет следующий вид: GENERATE FN $имя.
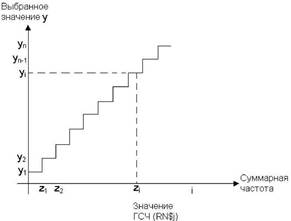
В качестве значения случайной величины выбирается такое yi, для которого полученное значение ГСЧ < zi. Геометрическая интерпретация розыгрыша случайной величины приведена на рис.1.1.
Рис. 1.1
Равномерное непрерывное распределение
В случае моделирования непрерывных случайных величин их значения находят из решения уравнения:
Ui = F(xi), (2)
где Ui –случайная величина, равномерно распределенная в интервале [0,1]; F(xi) – функция распределения искомой случайной величины.
Такой способ получил название "Способ обратной функции", так как требует отыскания функции, обратной к F(xi). Для данного распределения функция плотности распределения имеет вид:
f(x) =1/(b–a), a ≤ x≤ b; f(x) = 0, x<a , x > b.
Функция распределения получается интегрированием f(x):
F(xi) = 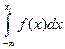 (x)dx (3)
(x)dx (3)
В GPSS равномерно распределенная в интервале [a;b] непрерывная случайная величина моделируется в виде (табл.1.2) Таблица 1.2
| 1 ... 7 | 8 ... 18 | 19 ... |
| имя | FUNCTION | RN$j , C2 |
| 0 , y1 / 1, y2 |
где y1 – минимальное значение случайной величины, равное a; y2 – максимальное значение, равное b + 1 .
Ссылка на функцию имеет следующий вид: GENERATE FN $ имя .
Геометрическая интерпретация розыгрыша непрерывной случайной величины приведена на рис.1.2.
Для моделирования непрерывной случайной величины средствами языков программирования необходимо вычислить F(xi) из уравнения (3) и, подставив полученное значение в (2), решить уравнение (2) относительно xi. Полученное выражение легко программируется.