Математические операции с передаточными функциями
Цель работы: Изучить прямое и обратное преобразование Лапласа, принципы получения передаточных функций и математические операции с ними в программе Matlab.
Задание:
а) По заданному преподавателем варианту (см. таблицу 4.1) выполнить последовательное, параллельное и встречно-параллельное соединение передаточных функций.
б) Получить графики переходных процессов для всех вариантов соединения.
в) Сделать выводы по работе.
Основные положения
Элементы систем автоматического регулирования обычно описываются передаточными функциями.
Передаточной функцией называется отношение изменения выходной величины к изменению входной, преобразованной по Лапласу.
Дифференциальное уравнение, представляющее математическую модель системы регулирования имеет следующий вид:
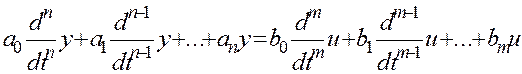 (4.1)
(4.1)
Где 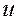 и
и 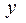 - входной и выходной сигналы системы регулирования.
- входной и выходной сигналы системы регулирования.
Преобразование Лапласа выполняется с помощью формулы:
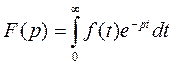
f(t) – оригинал
F(p) – изображение по Лапласу
В операторной форме это уравнение (1) будет следующим:
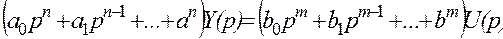 , (4.2)
, (4.2)
где, – 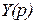 ,
, 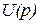 – изображение входного и выходного сигналов.
– изображение входного и выходного сигналов.
Определим передаточную функцию системы регулирования:
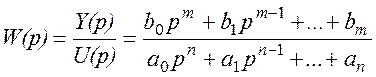 . (4.3)
. (4.3)
Порядок числа n больше или равно m.
Рассмотрим несколько простых уравнений.
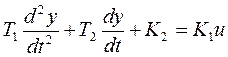 (4.4)
(4.4)
Преобразуем по Лапласу.
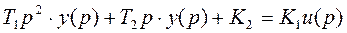 (4.5)
(4.5)
Найдём передаточную функцию
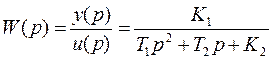 (4.6)
(4.6)
Те же операции проделаем и с уравнениями (4.7), (4.10), (4.13).
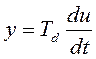 (4.7)
(4.7)
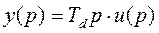 (4.8)
(4.8)
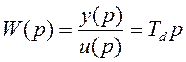 (4.9)
(4.9)
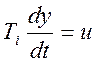 (4.10)
(4.10)
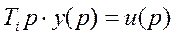 (4.11)
(4.11)
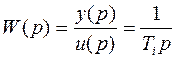 (4.12)
(4.12)
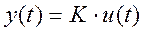 (4.13)
(4.13)
W(p)=K (4.14)
В программе Matlab передаточные функции создаются достаточно легко в строке команд. Например, если в уравнении (4.4) коэффициенты Т1, Т2, К2, К1 равны 2, 5, 1 и 1, то выполняется следующая операция:
>> w1=tf(1,[2 5 1])
Transfer function:
1
---------------
2 s^2 + 5 s + 1
>>
В англоязычных странах оператор Лапласа (p) обозначается (s).
Для уравнения (4.7) при 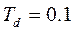
>> w2=tf([.1 0],[1])
Transfer function:
0.1 S
>>
С передаточными функциями работать значительно проще, чем с дифференциальными уравнениями. Их можно складывать, вычитать, умножать и делить, чтобы потом выполнить обратное преобразование Лапласа (4.15) и получить результирующее уравнение.
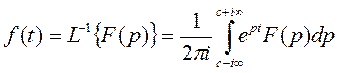 (4.15)
(4.15)
В Matlab имеются соответствующие функции прямого «laplace» и обратного преобразования Лапласа «ilaplace». Вычисления выполняются в символьной форме.
Примеры:
>> syms a t w s
>> laplace(exp(-a*t),t,s)
ans =
1/(s+a)
>> w=laplace(exp(-a*t),t,s)
w =
1/(s+a)
>> h=ilaplace(w,s,t)
h =
exp(-a*t)
>>
Как видно, вычисления выполняются корректно и совпадают с табличными.
Арифметические действия (+, -, /, *) с передаточными функциями могут быть выполнены в Matlab.
Пример: Рассмотрим две передаточные функции:
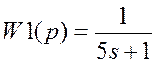
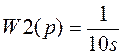
Получим их в строке команд Matlab.
>> w2
Transfer function:
1
----
10 s
>> w1=tf(1,[5 1])
Transfer function:
1
-------
5 s + 1
Выполним сложение.
>> w3=w1+w2
Transfer function:
15 s + 1
-------------
50 s^2 + 10 s
Тот же результат можно получить, применив оператор «parallel» вместо «+», что соответствует правилу сложения передаточных функций при их параллельном соединении.
Перемножим заданные функции:
>> w4=w1*w2
Transfer function:
1
-------------
50 s^2 + 10 s
Это же значение можно получить, применив оператор «series» вместо «*», что соответствует правилу умножения передаточных функций при их последовательном соединении.
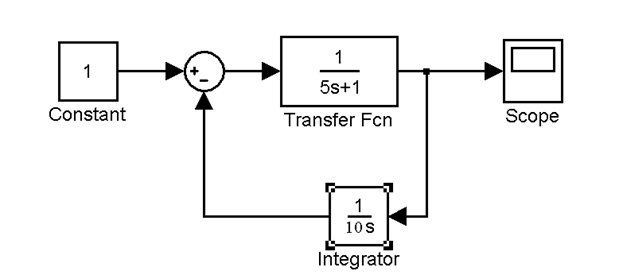
Если эти передаточные функции соединяются встречно-параллельно (Рис.4.1), то результирующая передаточная функция вычисляется по формуле:
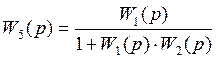 (4.16)
(4.16)
|
Знак «+» в знаменателе при отрицательной обратной связи и знак «-» при положительной.
В программе Matlab для этой операции есть оператор «feedback».
>> w5=feedback(w1,w2)
Transfer function:
10 s
-----------------
50 s^2 + 10 s + 1
Если положительная обратная связь, то в скобках добавляется «-1».
>> w5=feedback(w1,w2, -1)
Для полученных в результате всех операций функций можно построить их графики, если аргументом будет единичное ступенчатое возмущение. Для этого в программе Matlab предусмотрен оператор «step».
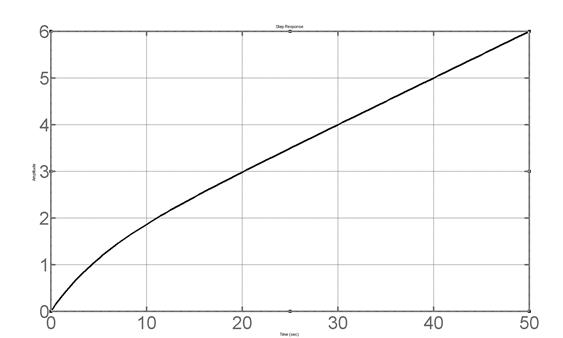
>> step(w3),grid on
Результат на рисунке 4.2.
|
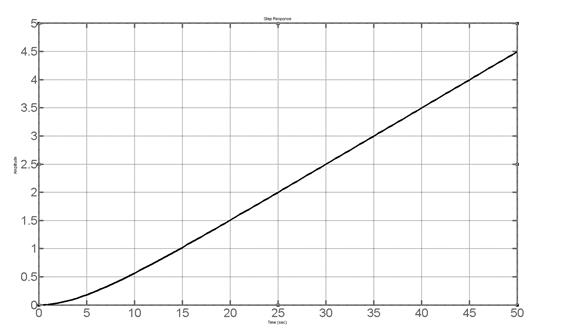
>> step(w4),grid on
Результат на рисунке 4.3.
|
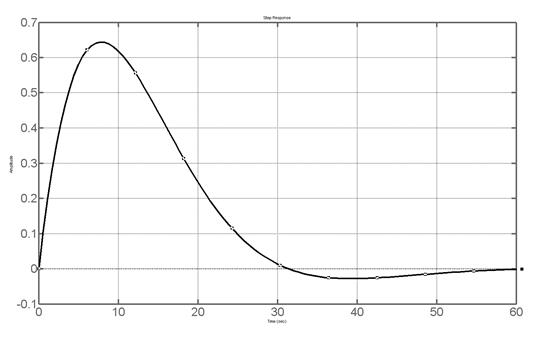
>> step(w5),grid on
>>
Результат на рисунке 4.4.
|
Порядок выполнения работы
1) По заданному преподавателем варианту (см. таблицу 4.1) выполнить последовательное, параллельное и встречно-параллельное соединение передаточных функций.
2) Получить последовательное, параллельное и встречно-параллельное соединение передаточных функций.
графики переходных процессов для всех вариантов соединения.
3) Скопировать результаты работы в файл формата *.doc для предъявления отчета и защиты работы.
4) В отчете сделать выводы по работе
Таблица 4.1
| Вариант | Функции | Параметры |
| 1 | 1-я (4.4), 2-я (4.10) | Т1=2, Т2=4, К2=1, К1=2, Ti=12 |
| 2 | 1-я (4.4), 2-я (4.10+4.13) | Т1= 1, Т2= 5, К2=1, К1= 1, Ti=12, K=5. |
| 3 | 1-я (4.4), 2-я (4.10+4.13) | Т1= 1, Т2= 15, К2= 5, К1= 1, Ti=7, K=9. |
| 4 | 1-я (4.4), 2-я (4.7+4.13) | Т1=1, Т2=5, К2=1, К1=1, Td=0. 2, K=5. |
| 5 | 1-я (4.4), 2-я (4.7+4.13) | Т1= 2, Т2= 10, К2= 2, К1=1, Td=0. 1, K=15. |
| 6 | 1-я (4.4), 2-я (4.13+4.10) | Т1=0. 2, Т2=5, К2= 2, К1=1, Ti=1 5, K= 2. |
| 7 | 1-я (4.4), 2-я (4.10+4.13) | Т1= 0.5, Т2= 25, К2=1, К1= 2, Ti= 25, K= 15. |
| 8 | 1-я (4.4), 2-я (4.13+4.10) | Т1= 0.1, Т2= 7, К2= 0.1, К1=1, Ti=12, K=1. |
| 9 | 1-я (4.4), 2-я (4.13+4.7) | Т1=2, Т2=3, К2=3, К1=1, Td=0. 1, K= 15. |
| 10 | 1-я (4.4), 2-я (4.13+4.7) | Т1=0.5, Т2=5, К2=1, К1=3, Td=0.2, K= 7. |
| 11 | 1-я (4.4), 2-я (4.10+4.13) | Т1=1, Т2= 25, К2= 3, К1=1, Ti=1 0, K= 1. |
| 12 | 1-я (4.4), 2-я (4.7+4.13) | Т1= 2, Т2= 10, К2= 2, К1=1, Td=0. 1, K=15. |
| 13 | 1-я (4.4), 2-я (4.10+4.13) | Т1= 1, Т2= 5, К2=1, К1= 1, Ti=12, K=5. |
| 14 | 1-я (4.4), 2-я (4.7+4.13) | Т1= 2, Т2= 10, К2= 2, К1=1, Td=0. 1, K=15. |
| 15 | 1-я (4.4), 2-я (4.10+4.13) | Т1= 1, Т2= 50, К2=1 0, К1= 1, Ti=22, K=2. |
| 16 | 1-я (4.4), 2-я (4.7+4.13) | Т1= 2, Т2= 10, К2= 2, К1=1, Td=0. 1, K=1 1. |
| 17 | 1-я (4.4), 2-я (4.10+4.13) | Т1=1, Т2=50, К2=1. 2, К1=1, Ti=30, K=5. |
| 18 | 1-я (4.4), 2-я (4.7+4.13) | Т1=2, Т2=10, К2=2, К1=1, Td=0.1, K=1. |
| 19 | 1-я (4.4), 2-я (4.10+4.13) | Т1=1, Т2=23, К2=1.5, К1=1, Ti=10, K=7. |
| 20 | 1-я (4.4), 2-я (4.7+4.13) | Т1=0.4, Т2=10, К2=6, К1=1, Td=0.1, K=12. |
| 21 | 1-я (4.4), 2-я (4.10+4.13) | Т1=1, Т2=21, К2=1, К1=1, Ti=1 7, K=5. |
| 22 | 1-я (4.4), 2-я (4.7+4.13) | Т1=0.3, Т2=10, К2=2. 5, К1=1, Td=0.1, K=3. |
| 23 | 1-я (4.4), 2-я (4.10+4.13) | Т1=0.2, Т2=16, К2=2, К1=1, Ti=15, K=2. |
| 24 | 1-я (4.4), 2-я (4.7+4.13) | Т1=2, Т2=10, К2=2, К1=1, Td=0.1, K=12. |
| 25 | 1-я (4.4), 2-я (4.10) | Т1=1, Т2=5, К2=1, К1= 2, Ti=12, K=25. |
Содержание отчета:
1. Передаточные функции при последовательном, параллельном и встречно-параллельном соединении заданных передаточных функций.
2. Графики полученных передаточных функций с четкой оцифровкой осей координат.
3. Выводы по работе.
ЛАБОРАТОРНАЯ РАБОТА №5
Исследование
частотных характеристик передаточных функций
Цель работы: Изучить принципы построения частотных характеристик передаточных функций в программе MATLAB .
Задание:
а) по заданному преподавателем варианту (см. таблицу 1) построить график АЧХ передаточной функции.
в). построить график ФЧХ передаточной функции.
с). построить графики АФЧХ передаточной функции.
Таблица 1.
| № п/п | Функция |
| 1 | W=1/(5s3+25s2+12s+2) |
| 2 | W=1/(12s3+30s2+12s+1) |
| 3 | W=2/(10s3+20s2+10s+1) |
| 4 | W=3/(5s3+30s2+7s+1) |
| 5 | W=1/(7s3+20s2+2s+1) |
| 6 | W=4/(12s3+10s2+12s+2) |
| 7 | W=2/(5s3+20s2+7s+1) |
| 8 | W=3/(12s3+20s2+5s+3) |
| 9 | W=2/(10s3+30s2+10s+1) |
| 10 | W=1/(20s3+20s2+12s+1) |
| 11 | W=2/(15s3+30s2+10s+1) |
| 12 | W=1/(30s3+20s2+12s+2) |
| 13 | W=1/(15s3+10s2+25s+1) |
| 14 | W=1/(5s3+25s2+10s+2) |
| 15 | W=2/(30s3+10s2+25s+2) |
| 16 | W=2/(5s3+10s2+7s+1) |
| 17 | W=3/(12s3+15s2+15s+3) |
| 18 | W=2/(10s3+30s2+10s+1) |
| 19 | W=1/(20s3+20s2+20s+1) |
| 20 | W=2/(15s3+30s2+10s+1) |
| 21 | W=1/(30s3+20s2+30s+2) |
| 22 | W=1/(15s3+5s2+10s+1) |
Основные положения
Частотные характеристики моделей, которые описаны соответствующими передаточными функциями, изучают, подавая на вход гармонический сигнал и измеряя величину амплитуды и сдвига фаз на выходе. Возьмём нижеследующую передаточную функцию второго порядка и в программе Simulink подадим на вход гармонический сигнал, изменяющийся по частоте (Рис.1).
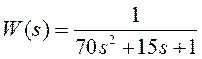
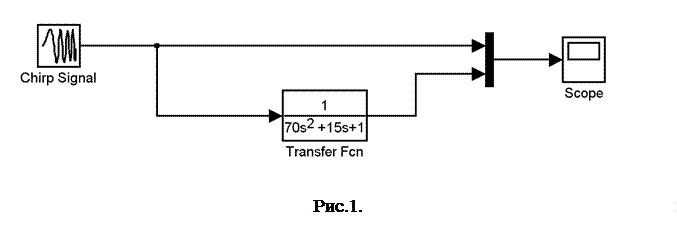
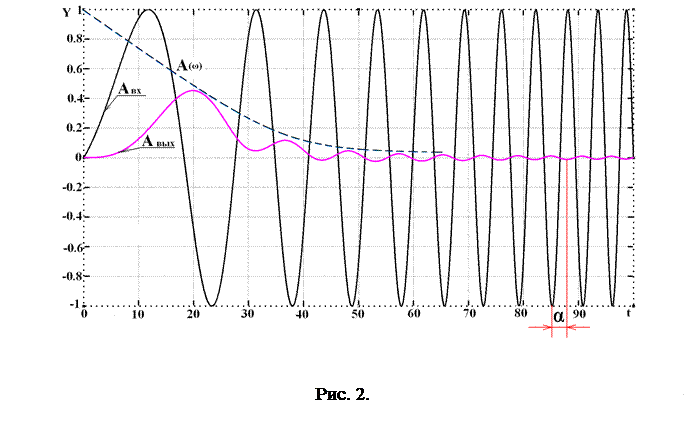 Результаты моделирования показаны на рисунке 2. На входе амплитуда сигнала остаётся постоянной, а на выходе наблюдается её уменьшение, в зависимости от частоты
Результаты моделирования показаны на рисунке 2. На входе амплитуда сигнала остаётся постоянной, а на выходе наблюдается её уменьшение, в зависимости от частоты 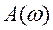 . Кроме того, при увеличении частоты гармонического сигнала, сдвиг фаз между входным и выходным сигналами увеличивается α(ω). Эти качественные характеристики хорошо видны на рисунке 2, но хотелось бы оценить их количественно. Математики нашли возможность оценить графически обе характеристики одновременно на комплексной плоскости. Впервые прямоугольную систему координат ввел француз Рене Декарт в своей работе «Рассуждение о методе» в 1637 году.
. Кроме того, при увеличении частоты гармонического сигнала, сдвиг фаз между входным и выходным сигналами увеличивается α(ω). Эти качественные характеристики хорошо видны на рисунке 2, но хотелось бы оценить их количественно. Математики нашли возможность оценить графически обе характеристики одновременно на комплексной плоскости. Впервые прямоугольную систему координат ввел француз Рене Декарт в своей работе «Рассуждение о методе» в 1637 году.
Как же передаточную функцию представить на комплексной плоскости. Рассмотрим передаточную функцию 1-го порядка:
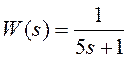
Подставим 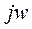 вместо s.
вместо s.
W(jw)=1/(5jw+1)
Умножим числитель и знаменатель на комплексно сопряжённое число
W(jw)=1/(5jw+1)=(5jw-1)/(5jw+1)(5jw-1)=(5jw-1)/(-25w2-1)
Поменяем знак в числителе и знаменателе.
W(jw)=1/(25jw+1)-5jw/(25jw+1)
В результате получили действительное и мнимое число.
Re(jw)= 1/(25w2+1)
 Im(jw)= -5jw/(25w2+1)
Im(jw)= -5jw/(25w2+1)
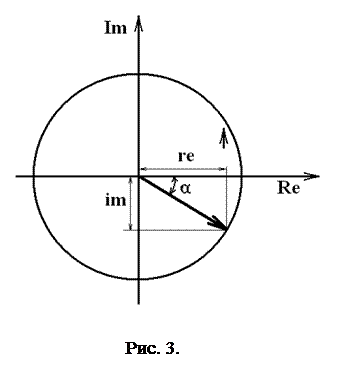
На рисунке 3 показана комплексная плоскость и полученные действительное re и мнимое число im для какой то определенной частоты w.
Для этой частоты можно рассчитать амплитуду сигнала a=sqrt(re.^2+im.^2) и сдвиг фаз α = atan(im./re);
В программе Matlab можно задать изменение частоты, рассчитать амплитуду и сдвиг фаз и построить график на комплексной плоскости.
w=0.001:.01:9;
re= 1./(25.*w.^2+1);
 im= -5.*w./(25.*w.^2+1);
im= -5.*w./(25.*w.^2+1);
a=sqrt(re.^2+im.^2);
fi=atan(im./re);
fig=360*fi/6.28
plot(re,im),grid on
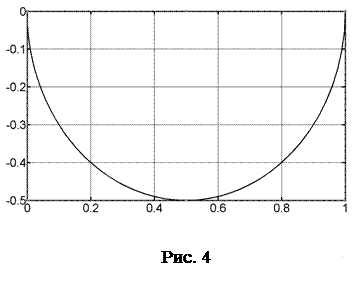
На рисунке 4 показан результат работы этой программы.
Конечно, можно напечатать график зависимости амплитуды от частоты a(w) (plot(w,a),grid on) и сдвига фаз от частоты fig(w) (plot(w,fig),grid on), который в программе из радиан преобразован в градусы. Как видно из графика на рисунке 4, амплитуда с ростом частоты убывает и стремится к нулю при увеличении частоты до ∞ для передаточной функции первого порядка, а угол сдвига фаз изменяется от нуля до 90о.
В программе Matlab есть для частотных исследований очень удобная функция F= freqs(num,den,w), где:
num – числитель передаточной функции,
den – знаменатель передаточной функции,
w – частота.
Здесь не нужно заменять оператор Лапласа на jw, а затем умножать числитель и знаменатель на комплексно сопряжённое число, что достаточно сложно уже для передаточных функций, начиная с четвертого порядка.
Используя функцию freqs(num,den,w), напишем программу Для расчета частотных характеристик передаточных функций.
w=0.0001:.001:9
den=[5 1];
num=[1];
ob=freqs(num,den,w);
v=imag(ob); % расчет мнимой части
u=real(ob); % расчет действительной части
f=atan(v./u); % расчет угла сдвига в радианах
a=sqrt(u.^2+v.^2); % расчет амплитуды
for i=1:2000 %
ug(i)=360*f(i)/6.28; % расчет угла сдвига в градусах
if f(i)>0
ug(i)=360*f(i)/6.28-180; % расчет угла сдвига в градусах >180о
end
am(i)=sqrt(u(i).^2+v(i).^2); % расчет амплитуды
end
plot(u,v),grid on % построение АФЧХ
При выполнении этой программы будет построен график, показанный на рисунке 4, то есть результат достигнут более быстрым способом. Тем более он удобен, если передаточная функция имеет более высокий порядок.
Содержание отчета:
1. График АЧХ передаточной функции..
2. График ФЧХ передаточной функции..
3. Графики АФЧХ передаточных функций, полученных путём снижения порядка до первого, начиная с заданного по варианту.
Например:
a)W1=3/(12s3+20s2+5s+3)
b) W2=3/(20s2+5s+3)
c) W3=3/(5s+3)
4. Выводы к каждому графику.
ЛАБОРАТОРНАЯ РАБОТА №6








