Определение коэффициента упругости и модуля упругости при деформации растяжения
Лабораторная работа № 1_09
Определение коэффициента упругости и модуля
упругости при деформации растяжения
Цель работы: определение коэффициента упругости и модуля упругости при деформации растяжения.
Приборы и принадлежности: прибор Лермонтова, проволока из исследуемого материала, набор грузов, микрометр, линейка.
Краткая теория
В теории упругости под словом «деформация» понимают всякое изменение в относительном расположении частиц твердого тела, возникающее под влиянием внешних сил.
Если внешние усилия малы, то с прекращением их действия вызываемая деформация исчезает. Если же они велики, то с прекращением их действия вызываемая ими деформация исчезает не полностью, обнаруживается так называемая остаточная деформация. Когда появляется первый след остаточной деформации, то говорят, что достигнут предел упругости.
Тела называются упругими, если предел упругости достигается при больших внешних усилиях (сталь, каучук, и т.д.) и неупругими, если предел упругости достигается уже при очень слабых усилиях (свинец).
Среди множества различных видов деформации следует отметить простейшие: деформация растяжения (сжатия) и деформация сдвига. Все остальные виды деформации имеют более или менее сложный характер. В случае, если деформации малы, то можно любую деформацию рассматривать как сумму некоторых растяжений и сдвигов.
При любом виде деформации, если она не очень велика по сравнению с размерами самого тела, возникает сила, которая старается вернуть тело в то состояние, в котором оно было до деформации. Эта сила и называется силой упругости. Сила упругости с вызывающей ее деформацией связана:
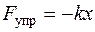 ,
,
здесь 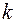 – коэффициент пропорциональности, называемый жесткостью тела;
– коэффициент пропорциональности, называемый жесткостью тела; 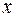 – удлинение тела.
– удлинение тела.
Рассмотрим деформацию растяжения. Под действием силы тяжести груза 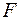 проволока или стержень длиной
проволока или стержень длиной 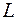 поперечного сечения
поперечного сечения 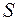 растягивается на величину
растягивается на величину 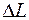 . Связь между удлинением проволоки
. Связь между удлинением проволоки 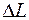 и силой
и силой 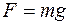 , вызывающей это удлинение, выражается законом Гука
, вызывающей это удлинение, выражается законом Гука
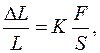
где 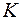 – коэффициент упругости;
– коэффициент упругости; 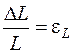 – относительная деформация,
– относительная деформация, 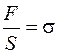 – усилие (механическое напряжение).
– усилие (механическое напряжение).
Коэффициентом упругости называется физическая величина, численно равная относительному удлинению при действии усилия равного единице.
Тогда модуль упругости (модуль Юнга) равен
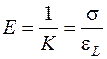 .
.
Модулем упругости называется физическая величина численно равная усилию, при котором относительное удлинение равно единице.
Под влиянием нагрузки проволока, растягиваясь, испытывает вместе с тем поперечное сжатие. Если диаметр проволоки уменьшается на величину 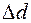 ,
,
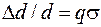 .
.
 Отношение относительного поперечного сжатия к относительному удлинению называется коэффициентом Пуассона:
Отношение относительного поперечного сжатия к относительному удлинению называется коэффициентом Пуассона:
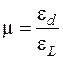 , где
, где 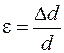 ,
, 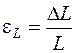 .
.
Теоретически для всех изотропных тел коэффициент Пуассона = 0,25.
Для определения модуля Юнга в этой работе используется прибор, схема которого изображена на рис. 1.
|
Верхний конец проволоки 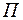 , изготовленный из исследуемого материала, прикреплен к кронштейну
, изготовленный из исследуемого материала, прикреплен к кронштейну 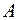 , а нижний – к раме, которая опирается на стержень индикатора
, а нижний – к раме, которая опирается на стержень индикатора 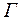 . Таким образом, удлинение проволоки можно измерить по отклонению стрелки индикатора. Натяжение проволоки можно менять, перекладывая грузы с платформы
. Таким образом, удлинение проволоки можно измерить по отклонению стрелки индикатора. Натяжение проволоки можно менять, перекладывая грузы с платформы 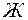 на платформу
на платформу 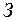 . Такая конструкция позволяет исключить влияние деформации кронштейна
. Такая конструкция позволяет исключить влияние деформации кронштейна 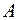 на показания индикатора при различных нагрузках.
на показания индикатора при различных нагрузках.
Измерения
1. Определите сечение проволок. Для этого измерьте ее диаметр микрометром не менее в 3–5 местах. Истинным диаметром считайте среднее из всех измерений 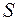 .
.
2. Измерьте начальную длину проволоки 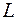 .
.
3. Снимите зависимость удлинения проволоки 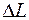 от ее натяжения при возрастающей нагрузке. Нулевое деление индикатора совмещают со стрелкой.
от ее натяжения при возрастающей нагрузке. Нулевое деление индикатора совмещают со стрелкой.
Последовательно нагружая площадку 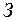 грузами одни за другим, проводят отсчет делений шкалы индикатора. Так проделывают для всех грузов, перекладывая их с площадки
грузами одни за другим, проводят отсчет делений шкалы индикатора. Так проделывают для всех грузов, перекладывая их с площадки 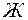 на площадку
на площадку 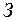 .
.
Для каждого значения нагрузки определите среднюю величину коэффициента 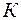 и модуль упругости
и модуль упругости 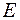 .
.
Результаты измерений и вычислений занесите в таблицу.
| № | 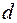 , м , м
| 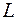 , м , м
| m, кг | 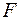 , Н , Н
| 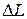 , м , м
| 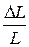
| 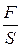 , Н/м2 , Н/м2
| 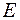 , Н/м2 , Н/м2
| 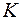 , м2/Н , м2/Н
|
| 1 |
|
| |||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 |
4. Используйте полученные результаты для построения графика зависимости изменения удлинения проволоки с изменением нагрузки и убедитесь, что имеет место линейная зависимость (закон Гука).
Результаты сравните с табличным значением.
Контрольные вопросы
1. Расскажите о явлении деформации. Приведите примеры.
2. Какие виды деформации вы знаете? Чем они отличаются друг от друга?
3. Что называется абсолютной величиной деформации и относительной деформацией для различных видов деформаций?
4. Что называется коэффициентом Пуассона? Его физический смысл?
5. Сформулируйте закон Гука. Связь между какими физическими величинами он дает? Физический смысл коэффициента упругости и модуля упругости?
6. Какие деформации называются упругими? Что называется пределом пропорциональности и пределом прочности? Нарисуйте диаграмму напряжений для какого-нибудь вещества и на нем покажите области, соответствующие пределу пропорциональности, пределу упругости, пределу текучести и пределу прочности.
7. Выведите формулу для расчета энергии упругой деформации.
8. Нарисуйте петлю упругого гистерезиса и объясните его.
9. Объясните явление деформации с точки зрения строения молекул.
10. Приведите примеры технического применения явления деформации.
11. Методика измерения. Анализ результатов.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Александров А.В., Яшкин А.Я. Курс общей физики. Механика. – М.: Просвещение, 1978. – с. 67-82.
2. Архангельский М.М. Курс физики. Механика. – М.: Просвещение, 1975. – Гл. ХI, §1-§5.
3. Савельев И.В. Курс общей физики. – Т.1. – М.: Наука, 1973 – §45.
4. Сивухин Д.В. Общий курс физики. – Т.1. – М.: Наука, 1974 – §73-81.
5. Стрелков С.П. Механика. – М.: Наука, 1975. §81-§91.








