Функция создания вероятностной НС
net=newpnn(P, T, spread). P – матрица входных векторов; T – матрица целевых векторов; spread – отклонение (по умолчанию 1,0).
Вспомогательные векторно-матричные функции
ind 2 vec ( ind ) – функция преобразования строки индексов (т.е. целых положительных чисел). Возвращается разреженная матрица с одним единичным элементом в каждом столбце, положение которого определяется исходным набором индексов. Аргумент – строка индексов ind.
Пример:
>> ind=[1 2 4 3]
ind =
1 2 4 3
>> vec=ind2vec(ind)
vec =
(1,1) 1
(2,2) 1
(4,3) 1
(3,4) 1
vec 2 ind ( vec ) – функция, обратная к функции ind 2 vec ( ind ).
Пример :
>> vec=[1 0 0 0;0 0 1 0;0 1 0 0;0 0 0 1]
vec =
1 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
>> ind=vec2ind(vec)
ind =
1 3 2 4
Пример создания вероятностной нейронной сети.
% Возьмем четыре 2-элементных входных вектора P (координаты четырех точек) и вектор ассоциированных с ними классов Tc:
>> P=[0 1 3 2; 3 1 2.5 4]
P =
0 1.0000 3.0000 2.0000
3.0000 1.0000 2.5000 4.0000
>> Tc=[1 2 3 4];
% Изобразим соответствующие точки на графике (см. рисунок 18)
>> plot(P(1,:),P(2,:),'.','markersize',30)
>> axis([-1 4 0 5])
>> hold on
% Подпишем точки в соответствии с их целевыми классами
>> for i=1:4,text(P(1,i)+0.1,P(2,i), sprintf('klass %g',Tc(i))), end
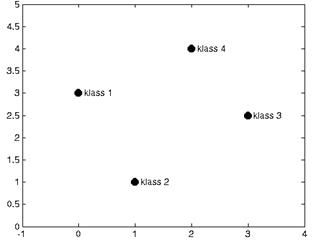
Рисунок 18 – Центры четырех классов
% Конвертируем индексы классов в разреженную матрицу T:
>> T=ind2vec(Tc);
% При создании вероятностной сети примем значение параметра spread =2,
% потому что это примерно равно среднему расстоянию между имеющимися точками.
>> spr=2;
% Создадим вероятностную НС функцией newpnn :
>> net=newpnn(P,T,spr);
% Испытаем созданную НС на входных векторах. Предварительно закроем
% окно с графиком, чтобы нарисовать новый.
>> A=sim(net,P);
% Конвертируем выходную матрицу в индексы классов:
>> Ac=vec2ind(A);
% Построим новый график с надписями классов, определенных сетью (см.
% рисунок 19)
>> plot(P(1,:),P(2,:),'.','markersize',30)
>> axis([-1 4 0 5])
>> hold on
>> for i=1:4,text(P(1,i)+0.1,P(2,i), sprintf('klass %g',Ac(i))), end
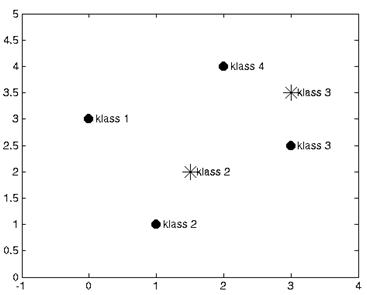
Рисунок 19 – Результаты классификации данных нейронной сетью
% Попробуем классифицировать при помощи созданной НС новые точки:
>> p=[1.5;2];
>> a=sim(net,p);
>> ac=vec2ind(a);
>> plot(p(1),p(2),'r*','markersize',15)
>> text(p(1)+0.1,p(2), sprintf('klass %g',ac))
>> p=[3;3.5];
>> a=sim(net,p);
>> ac=vec2ind(a);
>> plot(p(1),p(2),'r*','markersize',15)
>> text(p(1)+0.1,p(2), sprintf('klass %g',ac))
% Сеть справилась с новыми образцами успешно (см. рисунок 19).
Создайте вероятностную нейронную сеть для классификации образцов по трем заданным классам:
| Классы | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | ||||
| X | Y | X | Y | X | Y | X | Y | |
| Класс 1 | 0 | 2 | 1 | 2 | 3 | 2 | 1 | 1 |
| Класс 2 | 2 | 4 | 1 | 4 | 1 | 4 | 1 | 3 |
| Класс 3 | 2 | 0 | 3 | 3 | 5 | 4 | 3 | 1 |
| Классы | Вариант 5 | Вариант 6 | Вариант 7 | |||
| X | Y | X | Y | X | Y | |
| Класс 1 | 4 | 2 | 2 | 2 | 1 | 1 |
| Класс 2 | 2,5 | 4 | 4 | 4 | 3 | 1 |
| Класс 3 | 1 | 2 | 4 | 2 | 3 | 3 |
| Классы | Вариант 8 | Вариант 9 | Вариант 10 | |||
| X | Y | X | Y | X | Y | |
| Класс 1 | 2 | 1 | 4,5 | 3 | 1 | 4 |
| Класс 2 | 3 | 3 | 1 | 2 | 6 | 3 |
| Класс 3 | 4,5 | 1,5 | 3 | 0 | 3 | 1 |
Контрольные вопросы
1. В чем состоит математическое содержание задачи классификации образцов?
2. Какова архитектура вероятностной нейронной сети? Перечислите ее достоинства и недостатки.
3. Перечислите основные и вспомогательные функции Matlab для работы с вероятностными нейронными сетями.
7 Лабораторная работа № 7
СЛОИ КОХОНЕНА (6 часов)
7.1 Цель работы: Получить практические навыки создания и использования нейронных сетей со слоем Кохонена и самоорганизующихся карт признаков для решения задачи классификации образцов.
7.2 Задача кластеризации и поиска зависимостей
Кроме задачи классификации, нейросети широко используются для поиска зависимости в данных и кластеризации. Кластеризация – это разбиение набора примеров на несколько компактных областей (кластеров), причем принадлежность образцов конкретным кластерам заранее неизвестна. Кластеризация позволяет представить неоднородные данные в более наглядном виде и использовать далее для исследования каждого кластера различные методы. Например, таким образом можно выявить фальсифицированные страховые случаи, отчетность недобросовестных предприятий, проанализировать случаи производственного травматизма и т.д.
7.3 Слой Кохонена. Слой Кохонена функционирует по правилу "победитель получает все". Для любого конкретного входного вектора один и только один нейрон Кохонена выдает единицу, все остальные выдают нуль. Активность каждого нейрона Кохонена представляет собой вычисление расстояния между входным сигналом и вектором весов нейрона: 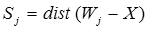
где Sj – активность j-го нейрона Кохонена, Wj=(w1j,…, wnj) – вектор весов j-го нейрона Кохонена, X=(x1,…, xn) – вектор входного сигнала.
Нейрон Кохонена с минимальным значением Sj является "победителем". Его выход равен единице, у остальных он равен нулю.
7.4 Обучение слоя Кохонена . Слой Кохонена классифицирует входные векторы в группы схожих. Это достигается с помощью такой подстройки весов слоя Кохонена, что близкие входные векторы активизируют один и тот же нейрон данного слоя.
Слой Кохонена обучается без учителя (самообучается). В результате самообучения слой приобретает способность разделять несхожие входные векторы. Какой именно нейрон будет активизироваться при предъявлении конкретного входного сигнала, заранее предсказать нельзя.
При обучении слоя Кохонена на его входы последовательно подаются входные вектора. Для каждого образца сначала выявляется нейрон, наиболее близкий к входному сигналу, затем он объявляется "выигравшим", после чего его веса подстраиваются таким образом, чтобы разница между его весами и входным сигналом стала еще меньше.
Как правило, обучающее множество включает много сходных между собой входных векторов, и сеть должна обучиться активизировать один и тот же нейрон Кохонена для каждого из них. Веса этого нейрона должны получаться усреднением входных векторов, которые должны его активизировать.
7.5 Самоорганизующаяся карта признаков
Самоорганизующаяся карта признаков имеет входные элементы, число которых соответствует размерности входных векторов, и набор выходных элементов (слой Кохонена), которые служат в качестве прототипов кластеров и называются "кластерными элементами". Входные элементы предназначены только для того, чтобы распределять данные входного вектора между нейронами слоя Кохонена. Часто удобно интерпретировать веса кластерных элементов как значения координат, описывающих положение кластера в пространстве входных данных.
Карта признаков проходит два этапа обучения. На первом этапе элементы упорядочиваются так, чтобы отражать пространство входных элементов, а на втором этапе происходит уточнение их позиций. В начале обучения карта выглядит сильно "измятой", в ходе обучения она постепенно разворачивается и расправляется.
Обычно число кластерных элементов выбирают значительно меньшим, чем число учебных образцов, поскольку целью работы является получение упрощенной модели множества данных. К концу обучения кластерные элементы обеспечивают "информационную сводку" по пространству входных образцов.
7.6 Изучаемые функции . Функции создания НС
net=newc(PR, S, KLR, CLR) – функция создания слоя Кохонена. Функция использует аргументы: PR – Rх2 матрица минимальных и максимальных значений для R входных элементов, S – число нейронов, KLR – коэффициент обучения Кохонена (по умолчанию 0,01), CLR – коэффициент "справедливости" (по умолчанию 0,001).
net=newsom(PR, [D1, D2,…], TFCN, DFCN, OLR, OSTEPS, TLR, TND) – функция создания самоорганизующейся карты с аргументами: PR – Rх2 матрица минимальных и максимальных значений для R входных элементов, Di – размеры i-го слоя, по умолчанию [5 8], TFCN – топологическая функция, по умолчанию 'hextop', DFCN – функция расстояния, по умолчанию 'linkdist',
 OLR – коэффициент обучения фазы упорядочивания, по умолчанию 0,9, OSTEPS – число шагов фазы упорядочивания, по умолчанию 1000, TLR – коэффициент упорядочивания фазы настройки, по умолчанию 0,02, TND – расстояние для фазы настройки (по умолчанию 1).
OLR – коэффициент обучения фазы упорядочивания, по умолчанию 0,9, OSTEPS – число шагов фазы упорядочивания, по умолчанию 1000, TLR – коэффициент упорядочивания фазы настройки, по умолчанию 0,02, TND – расстояние для фазы настройки (по умолчанию 1).
Вспомогательные функции
hextop( dim1, dim2,…, dimN) – функция размещения нейронов в узлах гексагональной (шестиугольной) решетки. Возвращает матрицу, содержащую N строк и (dim1 х dim2 х…х dimN) столбцов с координатами нейронов
plotsom( pos) – функция возвращает графическое представление расположения нейронов в самоорганизующихся картах.
Пример: pos = hextop(3,4)
pos =
0 1.0000 2.0000 0.5000 1.5000 2.5000 0 1.0000 2.0000 0.5000 1.5000 2.5000
0 0 0 0.8660 0.8660 0.8660 1.7321 1.7321 1.7321 2.5981 2.5981 2.5981
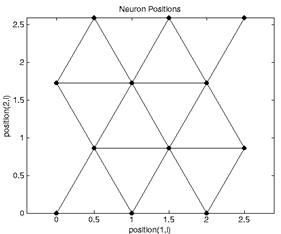
>> plotsom(pos) % Результат см. на рисунке 20
Рисунок 20 – Результат выполнения функции plotsom
7.7 Порядок выполнения работы
1. Кластеризация данных. Исходные данные приведены в таблице 3.
Таблица 3 – Исходные данные для кластеризации
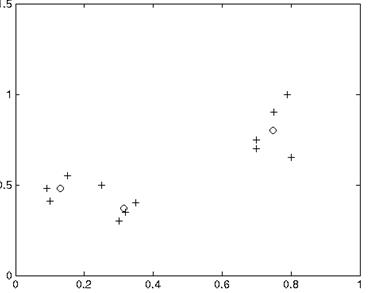
| x | 0.09 | 0.1 | 0.15 | 0.3 | 0.35 | 0.32 | 0.25 | 0.7 | 0.7 | 0.8 | 0.75 | 0.79 |
| y | 0.48 | 0.41 | 0.55 | 0.3 | 0.4 | 0.35 | 0.50 | 0.7 | 0.75 | 0.65 | 0.9 | 1 |
% Нанесем данные на график, установим размеры осей:
>> plot(P(1,:),P(2,:),'+r');
>> axis([0 1 0 1.5]);
>> hold on;
% На графике видны три кластера. Создадим слой Кохонена, состоящий из 3-х нейронов:
>> net=newc([0 1;0 1],3,0.1);
% Установим количество эпох обучения:
>> net.trainParam.epochs=10;
% запишем в массив w веса слоя Кохонена
>> w=net.IW{1};
% Нанесем их на график. Сеть еще не обучена, поэтому все веса изображены в виде одной точки посредине исследуемой области
>> h=plot(w(:,1),w(:,2),'ob');
% Запустим обучение сети. Сеть обучается самостоятельно (без учителя). Задание целевых векторов не требуется
>> net=train(net,P);
TRAINR, Epoch 0/10
TRAINR, Epoch 10/10
TRAINR, Maximum epoch reached.
% Запишем веса в массив w:
>> w=net.IW{1};
% Удалим точку, изображавшую веса необученного слоя Кохонена:
>> delete(h);
% Нанесем на график веса обученных нейронов (см. рисунок 21). Теперь веса нейронов слоя Кохонена соответствуют центрам кластеров опытных данных
>> h=plot(w(:,1),w(:,2),'ob');
% Подпишем классы в соответствии с решением сети:
>> W=w';
>> for i=1:3, text(w(i,1)+0.01,w(i,2), sprintf('k %g',vec2ind(sim(net,W(:,i))))),end
 % Проверим способность сети к классификации на данных, как входящих в обучающую выборку, так и новых:
% Проверим способность сети к классификации на данных, как входящих в обучающую выборку, так и новых:
>> p=[0.25;0.5];
>> a=sim(net,p)
a =
(3,1) 1
>> plot(p(1),p(2),'k*');
>> p=[0.2;0.5];
a=sim(net,p)
a = (2,1) 1
>> plot(p(1),p(2),'k*');
Рисунок 21 – Выявленные сетью центры кластеров (о)
>> p=[0.4;0.5];
a=sim(net,p)
a =
(3,1) 1
>> plot(p(1),p(2),'k*');
>> p=[0.8;0.75];
a=sim(net,p)
a = (1,1) 1
>> plot(p(1),p(2),'k*');
% По желанию можно преобразовывать разреженную матрицу решения сети в натуральный индекс при помощи функции vec2ind.
2. Пример создания самоорганизующейся карты.
% Сгенерируем тестовые данные - 1000 случайных точек в диапазоне координат (-1,1) и нанесем их на график:
>> P=rands(2,1000);
>> plot(P(1,:),P(2,:),'+r')
% Создадим самоорганизующуюся карту размером 5 х 6 нейронов:
 >> net=newsom([0 1;0 1],[5 6]);
>> net=newsom([0 1;0 1],[5 6]);
% Нанесем веса нейронов на график. Карта еще не обучилась, поэтому все веса изображены в виде единственной точки
>> plotsom(net.iw{1,1},net.layers{1}.distances)
% Установим количество эпох обучения = 1. Так как данных много, достаточно 1 эпохи обучения. В более сложных ситуациях количество эпох для полной организации карты может составлять 100-200
>> net.trainParam.epochs=1;
% Запустим механизм самообучения
>> net=train(net,P);
TRAINR, Epoch 1/1; TRAINR, Maximum epoch reached.
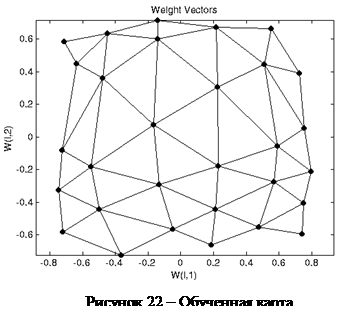
% Изобразим полученную в результате обучения карту на графике (см. рисунок 22)
>> plotsom(net.iw{1,1},net.layers{1}.distances)
% Теперь если мы сформируем произвольный вектор входа, то самоорганизующаяся карта Кохонена должна указать его принадлежность тому или иному кластеру (классу):
>> p=[0.5;0.3];
>> a=sim(net,p)
a = (16,1) 1
Указанный вектор принадлежит шестнадцатому кластеру.
1 Создайте слой Кохонена для кластеризации входных данных:
| 1 вариант | 2 вариант | 3 вариант | 4 вариант | 5 вариант | |||||
| x | y | x | y | x | y | x | y | x | y |
| 1 | 1 | 7,5 | 1 | 1,5 | 1 | 1,5 | 1 | 1,5 | 1 |
| 2 | 2 | 8 | 2 | 2,5 | 2 | 2,5 | 2 | 2,5 | 2 |
| 3 | 1 | 8,5 | 1 | 2,5 | 1 | 2 | 3 | 2 | 3 |
| 1,5 | 10 | 4,5 | 4,5 | 5,5 | 4,5 | 5,5 | 4,5 | 7 | 1,5 |
| 5 | 5 | 3,5 | 5 | 4,5 | 4,5 | 4,5 | 4,5 | 6,5 | 2 |
| 6 | 4,5 | 5 | 5,5 | 5 | 5,5 | 5 | 5,5 | 6 | 1,5 |
| 5,5 | 6 | 3,5 | 6 | 6 | 6 | 6 | 6 | 6 | 9 |
| 8 | 10 | 8 | 10 | 8,5 | 10 | 2 | 10 | 2 | 10 |
| 9 | 9 | 9 | 9 | 1,5 | 9 | 5 | 6,5 | 5,5 | 8,5 |
| 1 | 10 | 7,5 | 9 | 7,5 | 9 | 1,5 | 9 | 5,5 | 9,5 |
| 2 | 11 | 8,5 | 8 | 1 | 8 | 1 | 8 | 1 | 8 |
| 3 | 10 | 7,5 | 10 | 7,5 | 10 | 1 | 10 | 1 | 10 |
| 6 вариант | 7 вариант | 8 вариант | 9 вариант | 10 вариант | |||||
| x | y | x | y | x | y | x | y | x | y |
| 1,5 | 3 | 1,5 | 1 | 1,5 | 7,5 | 2 | 6 | 1,5 | 1,5 |
| 1 | 4,5 | 2,5 | 2 | 2,5 | 1,5 | 2 | 7 | 1 | 6,5 |
| 2 | 5 | 2,5 | 1 | 6,5 | 4 | 5,5 | 5 | 4 | 2,5 |
| 7 | 1,5 | 5,5 | 4,5 | 2 | 6 | 8 | 1 | 8 | 4 |
| 6,5 | 2 | 4,5 | 4,5 | 3 | 7,5 | 3 | 8 | 3,5 | 1,5 |
| 4,5 | 8 | 5 | 5,5 | 2 | 9 | 1 | 1 | 1,5 | 7 |
| 6 | 9 | 6 | 6 | 9 | 2,5 | 5 | 3,5 | 7 | 3,5 |
| 5 | 10,5 | 8,5 | 10 | 8 | 3 | 8 | 2 | 7,5 | 5 |
| 5,5 | 8,5 | 1,5 | 9 | 2,5 | 3 | 4,5 | 4,5 | 2,5 | 2 |
| 5,5 | 9,5 | 7,5 | 9 | 9 | 4 | 1,5 | 2 | 2 | 6 |
| 1 | 6 | 1 | 8 | 3 | 2,5 | 2 | 1 | 8,5 | 5 |
| 4,5 | 9,5 | 7,5 | 10 | 7,5 | 5 | 9 | 2,5 | 2,5 | 1 |
2 Создайте самообучающуюся карту признаков для кластеризации данных. Тестовые данные сгенерируйте случайным образом в квадрате (-1,1)´(-1,1) в количестве:
| 1 вариант | 2 вариант | 3 вариант | 4 вариант | 5 вариант |
| 50 | 100 | 150 | 200 | 250 |
| 6 вариант | 7 вариант | 8 вариант | 9 вариант | 10 вариант |
| 300 | 350 | 400 | 450 | 500 |
Контрольные вопросы
1. В чем суть задачи кластеризации образцов?
2. Что из себя представляет слой Кохонена, самоорганизующаяся карта признаков? Как они обучаются?
3. Приведите функции Matlab для работы со слоем Кохонена, самоорганизующейся картой признаков.
Лабораторная работа № 8
Сеть Хопфилда
1.1. Цель работы
Научиться работать с сетью Хопфилда newhop, исследовать устойчивость сети и её сходимость.
1.2. Краткие теоретические сведения
Американский исследователь Хопфилд в 80-х годах 20-го века предложил специальный тип нейросетей. Названные в его честь сети Хопфилда являются рекуррентными или сетями с обратными связями и предназначены для распознавания образов. Обобщенная структура этой сети представляется, как правило, в виде системы с обратной связью выхода с входом.
В сети Хопфилда входные сигналы нейронов являются одновременно и выходными сигналами сети: xi(k)= yi(k-1), при этом возбуждающий вектор особо не выделяется. В классической системе Хопфилда отсутствует связь нейрона с собственным выходом, что соответствует 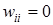 , а вся матрица весов является симметричной: w ij= wji
, а вся матрица весов является симметричной: w ij= wji
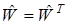 . (1)
. (1)
Симметричность матрицы весов гарантирует сходимость процесса обучения. Процесс обучения сети формирует зоны притяжения некоторых точек равновесия, соответствующих обучающим данным. При использовании ассоциативной памяти мы имеем дело с обучающим вектором 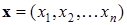 , либо с множеством этих векторов, которые в результате проводимого обучения определяют расположение конкретных точек притяжения (аттракторов).
, либо с множеством этих векторов, которые в результате проводимого обучения определяют расположение конкретных точек притяжения (аттракторов).
Каждый нейрон имеет функцию активации сигнум со значениями 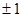 :
:
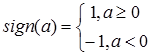 . (2)
. (2)
Это означает, что выходной сигнал i-го нейрона определяется функцией:
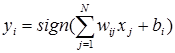 , (3)
, (3)
где N обозначает количество нейронов, N= n. Часто постоянная составляющая bi , определяющая порог срабатывания отдельных нейронов, равна 0. Тогда циклическое прохождение сигнала в сети Хопфилда можно представить соотношением:
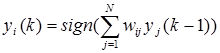 (4)
(4)
с начальным условием 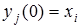 .
.
В процессе функционирования сети Хопфилда можно выделить два режима: обучения и классификации. В режиме обучения на основе известных обучающих выборок 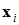 подбираются весовые коэффициенты wij. В режиме классификации при зафиксированных значениях весов и вводе конкретного начального состояния нейронов
подбираются весовые коэффициенты wij. В режиме классификации при зафиксированных значениях весов и вводе конкретного начального состояния нейронов 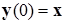 возникает переходный процесс, протекающий в соответствии с выражением (2) и заканчивающийся в одном из локальных устойчивых положений, задаваемом биполярным вектором со значениями
возникает переходный процесс, протекающий в соответствии с выражением (2) и заканчивающийся в одном из локальных устойчивых положений, задаваемом биполярным вектором со значениями 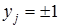 , для которого
, для которого 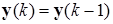 .
.
Обучение не носит рекуррентного характера. Достаточно ввести значения (правило Хебба) весов, выразив их через проекции вектора точки притяжения эталонного образа:
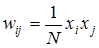 , (5)
, (5)
В соответствии с этим правилом сеть дает правильный результат при входном примере, совпадающим с эталонным образцом, поскольку:
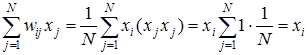 , (6)
, (6)
так как вследствие биполярности значений элементов вектора 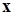 всегда
всегда 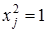 .
.
При вводе большого количества обучающих выборок 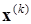 для k=1,2,… p веса wij подбираются согласно обобщенному правилу Хебба в соответствии с которым:
для k=1,2,… p веса wij подбираются согласно обобщенному правилу Хебба в соответствии с которым:
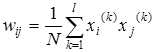 . (7)
. (7)
Благодаря такому режиму обучения веса принимают значения, определяемые усреднением множества обучаемых выборок. В случае множества обучаемых выборок актуальным становится вопрос о стабильности ассоциативной памяти.
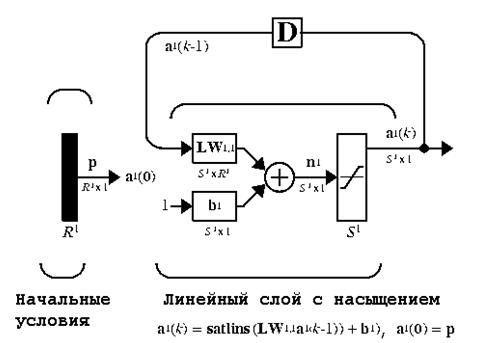
Сеть Хопфилда [2] является автоассоциативной сетью (рис. 12). Дискретная сеть Хопфилда имеет следующие характеристики: она содержит один слой элементов; каждый элемент связывается со всеми другими элементами, но не связан с самим собой; за один шаг работы обновляется только один элемент сети; элементы обновляются в случайном порядке; выход элемента ограничен значениями 0 или 1.
|
| Рис. 12. Схема архитектуры модифицированной сети Хопфилда |
1.3. Пример решения типовой задачи
Рассмотрим сеть Хопфилда [1] с четырьмя нейронами и определим четыре точки равновесия:
T = [+1 -1; -1 +1; +1 +1; -1 -1];
T=T';
plot(T(1,:),T(2,:),'rh','MarkerSize',13), hold on;
axis([-1.1 1.1 -1.1 1.1]);
title('Hopfield Network State Space');
xlabel('a(1)');
ylabel('a(2)');
net = newhop(T);
[Y,Pf,Af] = sim(net,4,[],T);
Y
Pf
Af
pause
color = 'rgbmy';
for i=1:25
a = {rands(2,1)};
[y,Pf,Af] = sim(net,{1 20},{},a);
record=[cell2mat(a) cell2mat(y)];
start=cell2mat(a);
plot(start(1,1),start(2,1),'kx',record(1,:),
record(2,:), color(rem(i,5)+1),'LineWidth',5)
end
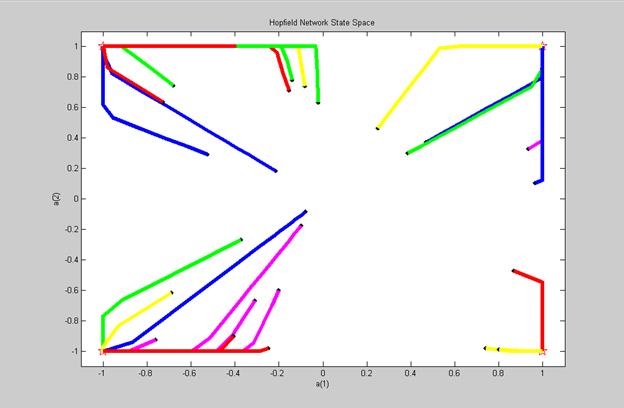
На рис. 13 показано поведение обученной сети при случайных начальных условиях a.
|
| Рис. 13. Поведение сети Хопфилда при случайных начальных условиях a |
1.4. Отчёт о выполнении работы
Отчёт о выполнении лабораторной работы №4 должен быть выполнен на листах формата А4 и содержать следующие результаты:
1. Исходные данные;
2. Текст программы с подробными комментариями;
3. Результаты моделирования (рис. 13);
4. Контрольный пример;
5. Краткие письменные ответы на контрольные вопросы, содержащиеся в приложении.
Контрольные вопросы для лабораторной работы № 8
1. Искусственный интеллект. Его истоки и проблемы.
2. Нейрофизиологические данные об обработке информации в биологических системах.
3. Искусственный нейрон. Идея и техническая реализация.
4. Модели нейронов. Типичные виды функций активации нейрона.
5. Многослойный персептрон.
6. Однонаправленные многослойные сети. Алгоритм обратного распространения ошибки.
7. Вывод конкретных формул алгоритма обратного распространения ошибки для двухслойных сетей с малым числом нейронов (2-3).
8. Градиентные методы. Алгоритм наискорейшего спуска. Недостатки метода. Метод моментов.
9. Радиальные нейронные сети. Обучение. Область применения.
10. Рекуррентные сети. Ассоциативная сеть Хопфилда. Обучение. Распознавание образов.
11. Сеть встречного распространения.
12. Обучение слоя Кохонена. Решение задач кластеризации.
13. Статистический подход к обучению нейронной сети. Машина Больцмана и ее модификации.
14. Применение нейронных сетей. Сбор данных для нейронных сетей.
15. Задача регрессии и прогнозирования временных рядов.
16. Основные характеристики пакета MATLAB. Простейшие вычисления. Работа с массивами. Графики функций. Сессия. М-файлы. Mat-файлы.
17. Нейронные сети в пакете MATLAB.








