НС с радиальными базисными функциями
(4 часа)
4.1 Цель работы: Получить практические навыки создания и использования НС с радиальными базисными элементами для решения задач аппроксимации и регрессии.
4.2 Сеть с радиальными базисными функциями
В сетях с радиальными базисными функциями используется подход, основанный на разбиении пространства гиперсферами. Каждый нейрон-радиальный элемент задается центром (некоторой разделяющей окружности) и радиусом (отклонением кривой разделения). По аналогии с обычным нейроном координаты центров радиальных элементов можно рассматривать как "веса", а радиус как "смещение".
НС с радиальными базисными элементами имеет один промежуточный слой, состоящий из радиальных элементов, каждый из которых воспроизводит гиперсферу, и выходной слой, состоящий из элементов с линейными функциями активации. Для моделирования любой функции достаточно взять определенное количество радиальных элементов.
НС с радиальными базисными элементами имеют ряд преимуществ. Они моделируют произвольную функцию с помощью всего одного промежуточного слоя, и обучаются на порядок быстрее, чем НС персептронного типа.
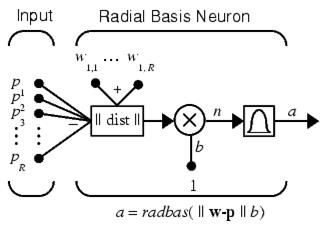Выражение для суммарного входа нейрона с радиальными базисными функциями отличается от суммарного входа обычных формальных нейронов (см. рисунок 9). Элемент 
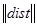на рисунке берет входной вектор p, однострочную матрицу весов входов w и вычисляет евклидово расстояние между ними Евклидово расстояние D между двумя векторами X и Y :
D = sum((x-y).^2).^0.5).
Рисунок 9 – Радиальный базисный нейрон
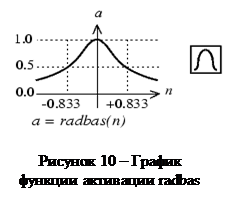
Радиальная базисная функция имеет максимум, равный 1, когда ее аргумент равен 0 (см. рисунок 10).
Когда расстояние между w и p уменьшается, выход функции возрастает. Таким образом, радиальный базисный нейрон действует как детектор, который выдает 1 только в том случае, когда вход p равен вектору весов w. Смещение b позволяет настраивать чувствительность радиального базисного нейрона. Например, если нейрон имеет смещение b=0,1, то он будет давать на выходе 0,5 для любого вектора p, расстояние от которого до вектора весов w составляет 8,33 (0,833/b).
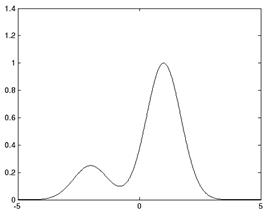
Произвольная криволинейная функция может быть аппроксимирована комбинацией радиальных базисных функций:
,
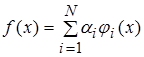где ji(x) – радиальная базисная функция (см. рисунок 11).
>> x = –5:0.01:5; %%
>> plot(x,(1/4)*radbas(x+2)+radbas(x–1));.
4.3 Изучаемые функции