Тақырыбы. Биологиялық және жасанды нейрон.
2 лек аяк жагы гана )))))))))))3лек Жандос Акжол
4 лек Улфат Улпан
5 Жадыра Азамат
6 Молдир Муха
7Жардем Асанали
8 Биржан Серик
2.3 Зертханалық жұмыстардың жоспары
№1 Зертханалық жұмыс
Тақырыбы. Биологиялық және жасанды нейрон.
Жұмыс мақсаты: биологиялық және жасанды нейронның құрылымын және жұмыс істеу принципін оқып үйрену.
Әдiстемелiк ұсыныстар .
Жасанды нейрон – енгізілген сигналдар жиынтығы бойынша шығу сигналын есептейтін қарапайым процессор. Салмақ коэффициентi бар немесе салмағы бар енгізілетін сигналдар ойлап-пiшiлген (взвешенный) байланыстар бойынша жiберіледi.
Жасанды нейронның құрамын көбейткiштер (синапстар), сумматорлар және түрлендiргiштер құрайды (жалпы жағдайда сызықты емес). Нейрондардың арасындағы байланыстарды синапстар жүзеге асырады және енгізілетін сигналдарды синапстың салмағына (бұл байланыстың күшін сипаттайтын сан) көбейтеді. Синапстың байланыстары бойынша сырттан енгізілген сигналдардың және басқа нейрондардан түсетiн сигналдардың қосуын сумматор орындайды. Жалпы жағдайда сызықты емес түрлендiргiш тек қана бiр аргументті сызықты емес функциясын жүзеге асырады - ол сумматордың шығуы ретінде алынады. Бұл функция активация функциясы немесе нейронның берiлiс функциясы деп аталады. Негiзiнде нейрон векторлық аргументтің скалярлық функциясын жүзеге асырады. Нейронның математикалық үлгiсi келесі формулалармен анықталады:
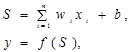
1. Matlab-тың анықтама жүйесінде келтiрiлген нейронның жұмыс істеу бағытымен танысыңыз
– D emo – Toolboxes – Neural Networks.
- Simple neuron and transfer functions (қарапайым нейрон және беріліс функциялар);
- Neuron with vector input (векторлық кірісі бар нейрон).
2. Берiлiс функцияның нейронның шығу сигналының мәніне ықпалын талқыланыңыз ( 1 кесте).
3. Neural Networks Matlab-тағы активация функцияларымен танысыңыз.
Жұмысты орындау тәртібі
1. 1 кестедегі келтірілген беріліс функциялардың графиктерін анықтаңыз.
2. 1-ші кестеде активацияның барлық функциялары үшiн енгізілетін және салмақтардың мәндері берілген, осы берілгендер үшін нейронның шығуын Excel – де есептеңiз. [-5,5] аралығында тиiстi жасанды нейронның схемасын бейнелеңiз.
1 Кесте – Нейрондарды активациялау функцияларының тiзiмi
| № | Функция атауы | Формула сы | Мәндер аумағы |
| 1 | Табалдырықты (Пороговая) hardlim |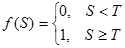 
| (0, 1) |
| 2 | Таңбалық (Знаковая) (сигнатурная) Hardlims |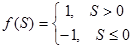 
| (-1, 1) |
| 3 | Сигмоидальдық (логистическая) logsig |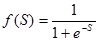 
| (0, 1) |
| 4 | Жартылай сызықтық (Полулинейная) poslin |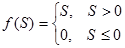 
| (0, ¥) |
| 5 | Сызықтық (Линейная) purelin |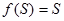 
| (-¥, ¥) |
| 6 | Радиальді-базистік (Радиальная базисная ) (гауссова) radbas |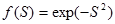 
| (0, 1) |
| 7 | Қанығумен жартылай сызықтық (Полулинейная с насыщением) satlin |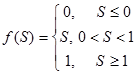 
| (0, 1) |
| 8 | Қанығумен сызықтық (Линейная с насыщением) satlins |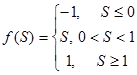 
| (-1, 1) |
| 9 | Гиперболалық тангенс (сигмоидальная) tansig |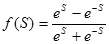 
| (-1, 1) |
| 10 | Үш бұрышты (треугольная) tribas |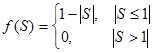 
| (0, 1) |
Тапсырма варианттары
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | |||||
| Х | W | X | W | X | W | X | W | X | W |
| 0,7 | -0,3 | 0,4 | 0,5 | 0,2 | -2,1 | 0,3 | 0,6 | 0,6 | 0,8 |
| 0,1 | 3,1 | 0,9 | -0,9 | 0,5 | 3,5 | 0,1 | 1,9 | 0,7 | -0,9 |
| 0,3 | 0,5 | 0,1 | 2,6 | 0,6 | -0,2 | 0,5 | 0,7 | 0,9 | 1,5 |
| b=0,9 | b=1,3 | b= –0.5 | b= 1,5 | b= – 0,7 | |||||
| Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 10 | |||||
| X | W | X | W | X | W | X | W | X | W |
| 0,2 | -1,1 | 0,2 | -1,1 | 0,3 | -1,5 | 0,5 | 0,2 | 0,1 | 1,8 |
| 0,5 | 0,8 | 0,5 | 0,8 | 0,7 | 2,4 | 1,1 | 2,1 | 1,7 | -1,9 |
| 0,4 | 0,6 | 0,4 | 0,6 | 1,6 | -3,2 | 1,9 | 0,3 | 2,9 | 0,5 |
| b=0,4 | b= –1 | b=0,3 | b= –2 | b= – 1,7 | |||||
3. Зерханалық жұмысында вариант бойынша берілгендерге барлық келтiрiлген Matlab-тың функцияларын орындаңыз.
Әдебиет нег. 8 [4-5], қос. 15 [1-62]
Бақылау сұрақтары
1. Биологиялық нейронның жұмыс істеу принципін және құрылымын сипаттаңыз.
2. Активацияның математикалық функцияларын атап өтіңіз. Олардың формулаларын және графиктерін, мәндердiң өзгеру облысын келтіріңіз.
3. Matlab Neural Networks –де активацияның қандай функциялары бар және активацияның функцияларының туындылары бар ма?
№ 2 Зертханалық жұмыс
Тақырыбы. Қарапайым нейрожелiлер. Персептрондар
2.1 Жұмыс мақсаты: Қарапайым нейрондық желілерді құруға және оларды пайдалануға үйрену. Нейрондық желімен жұмыс істеу үшiн графикалық функцияларын, қатенiң функцияларын, тағы басқа қосалқы функцияларын оқып білу және оларды қолданып практикалық дағдыларын алу.
2.2 Персептрондар
Нейрон, схема которого приведена на рисунке 2, называется нейроном персептронного типа, или просто персептроном. Как правило, персептроны имеют пороговую функцию активации. Нейронная сеть, состоящая из одного или нескольких слоев нейронов персептронного типа также называется персептроном.
Работа персептрона сводится к классификации входных сигналов, принадлежащих n-мерному гиперпространству, по некоторому числу классов. С математической точки зрения это происходит путем разбиения гиперпространства гиперплоскостями (в случае двумерного пространства разбиение осуществляется прямой). Задачи, которые может решать однослойный персептрон, называются линейно отделимыми.
Әдiстемелiк ұсыныстар
2.3 Зерттелетін функциялар. Нейрондық желісін жасау функциясы.
net = newp(PR, S, TF, LF) – персептронды құру функциясы. Персептрон – нейрондардан тұратын бiр қабатты нейрондық желi, әдетте оларда белсендiлiктiң (активация) табалдырықты функциясы болады.
Аргументтері: PR - R – кіріс элементтердiң ең төменгi және максимал мәндерiнен тұратын R х 2 матрицасы, S – нейрондар саны, TF – активацияны жасайтын функция, үнсіз бойынша 'hardlim', LF – оқыту функциясы, үнсіз бойынша 'learnp'.
Нейрондар қабаттарын баптау
Функциялар қосалқы болып табылады және басқа функциялармен қолданылады.
learnp(W, P, …) – персептронды оқыту алгоритімін жүзеге асыратын функциясы.
learnpn(W, P, …) – берілгендерді тұрақты ету әрекетімен персептронды үйретудің алгоритімін iске асыратын функция.
Қателердiң функциялары.
mae(E) – желiнiң орташа абсолюттiқ қатесiн қайтарады.
sse(E) – желiнiң қателер квадраттарының қосындысын қайтарады.
mse(E) – желiнiң орташа квадраттық ауытқуын қайтарады.
Барлық функциялары үшiн E-нің аргументі – желiнiң қателерiнiң матрицасы (T–Y), мұнда T – мақсаттық вектор, Y – желi модельдеуінің нәтижесі (опрос ).
Графикалық функциялар.
hintonw(W, maxw, minw) – салмақтар матрицасының хинтоновтың графигiн қайтаратын функция, онда әрбір салмақ коэффициентi тiк төртбұрыштың түрiнде көрсетiледi, оның аланы осы коэффициенттiн шамасына пропорционалды болады. Таңба (знак) тiк төртбұрыштың түсiмен көрсетiледi.
Аргументтер: W – салмақтар матрицасы, мiндеттi емес параметрлер maxw, minw – салмақтар матрицасының элементтерiнiң ең төменгi және ең жоғарғы мәндері.
Hintonwb (W, b, maxw,minw) – ұқсас функция, бiрақ графикада салмақ ғана емес, (b) орын ауыстыру да көрсетiледi
plotpv(P,T) – персептронның P кіретін және T мақсаттық векторларының график түрінде бейнесін қайтаратын функция.
plotpc(W,b) – персептрон шешiмінiң сызық графигiн қайтаратын функция. Аргументтер: W – салмақтар матрицасы , b –орын ауыстыру векторы. Рlotpv функциясымен бірге қолданылады.
Функция адаптации
[net, Y, E]=adapt(net, P, T) – выполняет адаптацию сети в соответствии с установками net.adaptFcn и net.adaptParam. Функция возвращает значения выходов Y и ошибку сети E. Аргументы: net – имя сети, P – входные векторы, T – выходные векторы.
Қолдануға арналған функциялар
Y=sim(net, P) – функция, моделирующая работу нейронной сети. Функция возвращает значения выходов Y. Аргументы: net – имя сети, P – ее входы.
gensim(net) – функция генерирует нейросетевой блок Simulink для последующего моделирования нейросети средствами этого пакета.
Нейрондық желілердің сипаттамалары
adaptFcn - определяет функцию, используемую при адаптации НС.
adaptParam - определяет параметры используемой функции адаптации (количество циклов настройки).
IW – массив, определяющий веса от входов к слоям НС.
b – массив, определяющий векторы смещений слоев нейронов.
2.4 Жұмысты орындау тәртібі
Барлық деректерді үйретушi және тексеретін жиындарға бөлшектеңіз. Классификацияны өткізетін персептронды жасаңыз. Графиктер түрінде нейрожелінің жұмыс істеуін көрсетіңіз.
2.4.1. Demo-Toolboxes-Neural Networks-та классификация есебімен таңысу.
- Decision boundaries (Граница решения).
Бірінші кластағы элементтерді ақ маркерлер белгілейді, қара – екіншіі. Диаграмма элементерін және шешу сызығын жылжытып қолданушы өзі қлассификация есептерін жасап шешімін алады. Ол үшін қойылған еепті шығарған кезде персептронның параметрлері автоматты түрде өзгереді,.
- Perceptron learning rule ( персептронды ұйретудің ережелерін қолдану).
Ақ және қара маркерлерін тасымалдап жаңа есептерді құруға болады. Нәтижесін алу үшін келесі пернелер қолданылады: "Learn" – бірлік векторды қолданып персептронды ұйрету; "Train" – 5 дейін ұйрету циклін қайталау; "Random" – кездейсоқ тәсілімен шешуді табу. Ауытқумен және ауытқусыз персептрон нұсқаларын таңдауға болады (Bias, No bias).
2.4.2. Matlab-та классификацияны өткізе алатын персептронды құру мысалы
Мысал ретінде максимальдық жылдамдылығына және максимальдық ұшып шығу салмағына тәуелді бомба тастайтын және истребитель ұшақтарына қлассификациялауды өткізетін есебін рәсімдейміз және шешімін табамыз. Самолет туралы берілген деректерді диаграммаға түсіреміз (3-сурет ).
Сызық арқылы бөлуді өткізетін есепті шешу қажет – провести прямую, которая разделит плоскость на две полуплоскости таким образом, что все точки первого класса (истребители) будут принадлежать одной полуплоскости, а все точки второго класса (бомбардировщики) будут принадлежать другой полуплоскости.
Для решения разделим имеющиеся данные на две группы. Первую часть используем для обучения созданного персептрона (обучающая выборка).
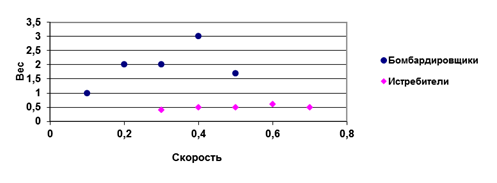
Рисунок 3 – Данные двух классов на плоскости
Вторую – для проверки правильности его работы после обучения (тестовая выборка).
>> P=[0.1 0.3 0.3 0.6 0.5; % Задаем 5 входных векторов – координат (x, y)
1 2 0.4 0.6 1.7] % пяти точек (обучающая выборка)
P = 0.1000 0.3000 0.3000 0.6000 0.5000
1.0000 2.0000 0.4000 0.6000 1.7000
>> T=[0 0 1 1 0] % Задаем целевой вектор принадлежности точек классам
T =
0 0 1 1 0
Ø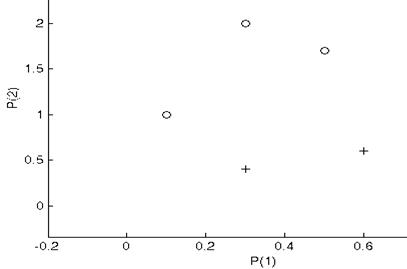 
Выводим график (см. рисунок 4). Точки, принадлежащие одному классу, изображены крестиками, другому классу – кружками.
>> plotpv(P,T)
Ø Создаем нейронную сеть, состоящую из одного персептрона с двумя входами
>> net=newp([0 1;0 2],1);
Ø Попытаемся выдать линию решения. Но созданный персептрон пока имеет нулевые веса и не сможет справиться с задачей:
>> linehandle=plotpc(net.IW{1},net.b{1})
>> E=1;