Аналитическое выравнивание по полиному второй степени
Данная модель имеет вид: 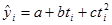
Для оценивания параметров тренда при 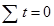 , применяют формулы (5.3) – (5.5). Тогда система примет вид (необходимые расчеты представлены в таблице столбцы 3-7):
, применяют формулы (5.3) – (5.5). Тогда система примет вид (необходимые расчеты представлены в таблице столбцы 3-7):
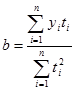 (5.3).
(5.3).
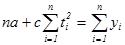 (5.4)
(5.4)
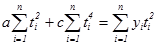 (5.5)
(5.5)
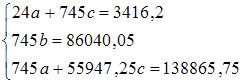
В результате решения системы получаем уравнение: 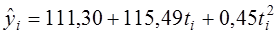 . Параметр
. Параметр 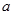 характеризует расчетное значение при t=0, т.е. расчетное значение составило 111,30 млн. р. Величина
характеризует расчетное значение при t=0, т.е. расчетное значение составило 111,30 млн. р. Величина 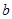 соответствует среднему абсолютному приросту уровней временного ряда, а параметр
соответствует среднему абсолютному приросту уровней временного ряда, а параметр 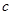 - половина абсолютного ускорения. Следовательно, можно сделать вывод, что в анализируемом периоде доходы бюджета возрастали в среднем за год на 115,49 млн. р. с абсолютным ускорением 0,9 млн. р.
- половина абсолютного ускорения. Следовательно, можно сделать вывод, что в анализируемом периоде доходы бюджета возрастали в среднем за год на 115,49 млн. р. с абсолютным ускорением 0,9 млн. р.
3 . Построить тренд – сезонную аддитивную или мультипликативную модель. Для всех построенных моделей с помощью средней относительной ошибки аппроксимации оценить их качество и дать прогноз на следующие два периода.
Прогнозирование по тренд – сезонной аддитивной модели
Проведем сглаживание временного ряда с помощью центрированной скользящей средней по формуле:
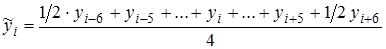
Рассчитаем абсолютные показатели сезонности по формуле 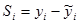 . Результаты расчетов скользящей средней и показателя сезонности представлены в таблице
. Результаты расчетов скользящей средней и показателя сезонности представлены в таблице
| период | доход yt | |||
| 2001 | I | 80,6 | y | Si |
|
| II | 90,5 |
|
|
|
| III | 95,5 |
|
|
|
| IV | 104,8 | 93,8375 | 1,6625 |
| 2002 | I | 88,5 | 95,9 | 8,9 |
| II | 99,1 | 98,05 | -9,55 | |
|
| III | 104,1 | 101,1375 | -2,0375 |
|
| IV | 120,9 | 105,1625 | -1,0625 |
| 2003 | I | 104,6 | 109,075 | 11,825 |
| II | 114,3 | 112,6625 | -8,0625 | |
|
| III | 117,6 | 116,55 | -2,25 |
|
| IV | 138,5 | 120,45 | -2,85 |
| 2004 | I | 118,2 | 123,3375 | 15,1625 |
| II | 123,8 | 125,9125 | -7,7125 | |
|
| III | 128,7 | 129,175 | -5,375 |
|
| IV | 153,5 | 131,9125 | -3,2125 |
| 2005 | I | 125,1 | 135,125 | 18,375 |
| II | 142,6 | 139,75 | -14,65 | |
|
| III | 146,9 | 144,75 | -2,15 |
|
| IV | 175,3 | 149,0375 | -2,1375 |
| 2006 | I | 137,6 | 153,375 | 21,925 |
| II | 164,8 | 158,8 | -21,2 | |
|
| III | 168,1 | 164,425 | 0,375 |
|
| IV | 199,1 |
|
|
Определим средние показатели сезонности по формуле: 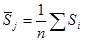 , т.е. для января средний показатель сезонности составит:
, т.е. для января средний показатель сезонности составит:
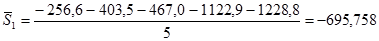 ,
,
для февраля:
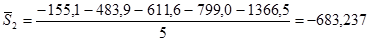
Аналогично рассчитывают для других месяцев .
Так как сумма средних показателей сезонности не равна нулю, проведем их корректировку по формуле:
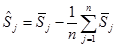 .
.
Скорректированный показатель сезонности для января составит:
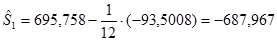 и т.д.
и т.д.
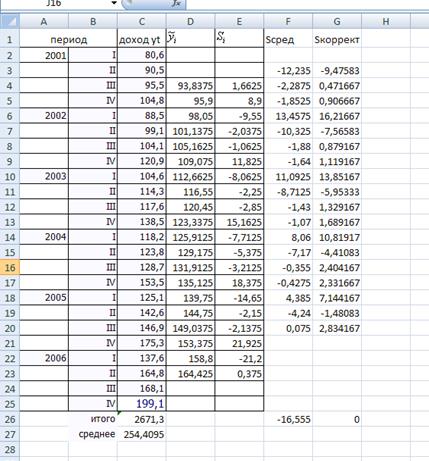
Результаты расчетов средних и скорректированных показателей сезонности заносим в таблицу
Таблица - Оценивание сезонной компоненты в аддитивной модели
5 задание
| Годы | |||
| y | x | ||
| 1 | 315,90 | 5,90 | |
| 2 | 331,00 | 6,90 | |
| 3 | 339,60 | 7,90 | |
| 4 | 363,80 | 9,30 | |
| 5 | 380,00 | 11,00 | |
| 6 | 389,30 | 11,90 | |
| 7 | 411,70 | 13,30 | |
| 8 | 431,60 | 14,30 | |
| 9 | 448,50 | 15,40 | |
| 10 | 462,54 | 16,79 | |
| 11 | 479,23 | 18,02 | |








