5Лабораторная работа 5 Моделирование временных рядов
Цель изучения темы: научитьсяопределять тип тенденции и выявлять наличие периодической составляющей во временном ряду, а также оценивать уровень сезонности, осуществлять фильтрацию периодических составляющих временного ряда и их моделирование. Научитсяоценивать тесноту и направление связи между показателями, представленными временными рядами. Строить модели регрессии по временным рядам, имеющим тенденцию, и прогнозировать на их основе.
Задание:
Для временного ряда финансового или социально-экономического показателя с помесячной или поквартальной динамикой требуется:
1) на основе графического анализа провести исследование компонентного состава временного ряда;
2) при обнаружении тенденции во временном ряду оценить параметры линейного и параболического тренда;
3) построить прогноз по тренд – сезонной аддитивной или мультипликативной модели;
4) построить прогноз по модели регрессии с включением фактора времени и фиктивных переменных;
5) по данным приложения Б для своего варианта оцените тесноту и направление связи между указанными признаками, а также постройте уравнение регрессии по первым разностям, по отклонениям от тренда и уравнение регрессии с включением фактора времени.
Для всех построенных моделей с помощью средней относительной ошибки аппроксимации оценить их качество и дать прогноз на следующие два периода.
Графический анализ исходного временного ряда (рисунок 5.1) свидетельствует о наличии трендовой компоненты, характер которой близок к линейному развитию: имеется устойчивая, ярко выраженная тенденция роста доходов бюджета Оренбургской области. Кроме того в ряду наблюдается сезонная составляющая с периодичностью 1 год (наименьшие значения доходов бюджета в январе каждого года).
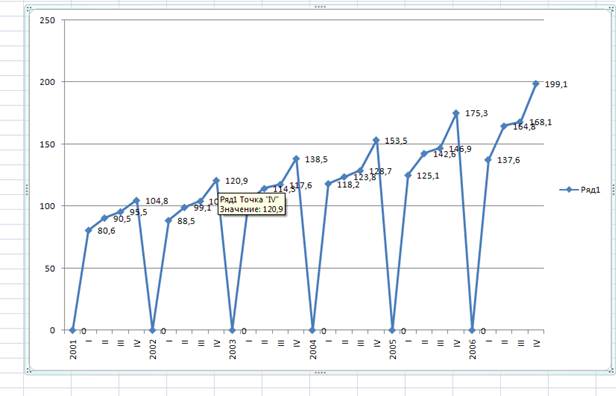
Рисунок 5.1 –Динамика доходов бюджета Оренбургской област 
и
2 При обнаружении тенденции во временном ряду оценить параметры линейного и параболического тренда
Аналитическое выравнивание по прямолинейному тренду
Уравнение прямолинейного тренда имеет вид: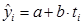 
.
При начале отсчета времени от середины ряда система нормальных уравнений упрощается и параметры уравнения определяют по формулам:
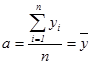(5.1)
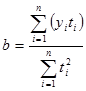(5.2)
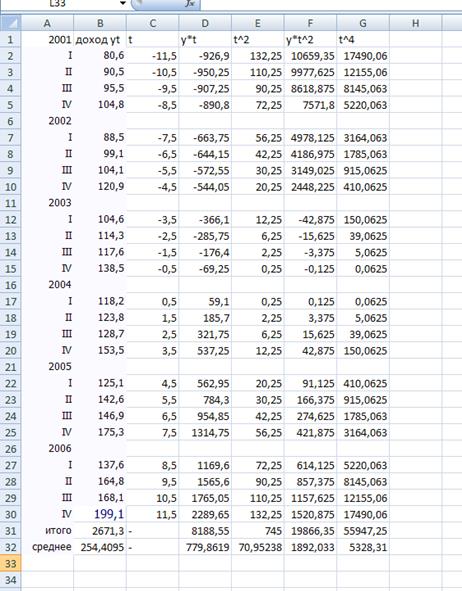
Необходимые расчеты представлены в таблице 5.1 (столбцы 3-5).
Тогда значения параметров составят:
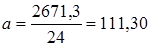
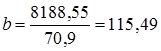
Уравнение тренда примет вид: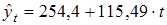 
. Согласно этой модели средний доход бюджета за анализируемый период составил 369,89 млн. р., а среднемесячный прирост доходов 34,53 млн. р.
Таблица –Расчет параметров линейного и параболического тренда
