Прогнозирование по тренд – сезонной мультипликативной модели
Так как амплитуда сезонных колебаний постепенно увеличивается, то для описания и прогнозирования динамики временного ряда можно использовать мультипликативную модель.
На первом этапе, как и при построении аддитивной модели, проведем сглаживание временного ряда с помощью центрированной скользящей средней по формуле.
На следующем этапе рассчитаем коэффициенты сезонности по формуле 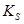 =
= 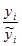 .
.
Результаты расчетов скользящей средней и коэффициента сезонности представлены в таблице 8.6.5.
Определяем средние показатели сезонности для одноименных кварталов (месяцев):
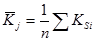 .
.
Таблица 8.6.5 - Разложение уровней ряда по мультипликативной модели
Так как сумма средних коэффициентов сезонности не равна 12, проведем их корректировку по формуле:
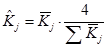 .
.
Так скорректированный коэффициент сезонности для января составит:
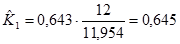 и т.д.
и т.д.
Результаты расчетов средних и скорректированных показателей сезонности заносим в таблицу 8.6.6.
Таблица 8.6.6 - Оценивание сезонной компоненты в мультипликативной модели 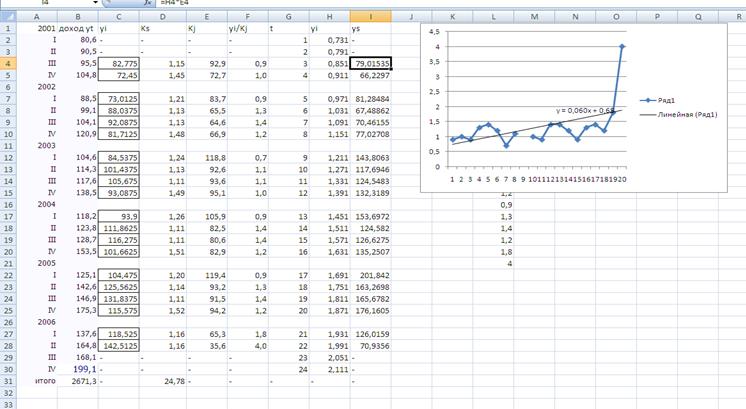
Так как сумма средних коэффициентов сезонности не равна4, проведем их корректировку по формуле:
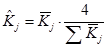 .
.
Результаты расчетов средних и скорректированных показателей сезонности заносим в таблицу 8.6.6.
Таблица 8.6.6 - Оценивание сезонной компоненты в мультипликативной модели
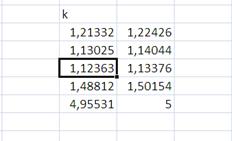
На следующем этапе определим десезоналированный ряд объема производства:
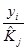 .
.
По десезоналированному временному ряду проводим аналитическое выравнивание по линейному тренду. Уравнение тренда имеет вид:
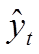 =0,671+0,060t.
=0,671+0,060t.
Затем рассчитываем тренд с учетом сезонности:
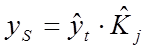 .
.
Результаты расчетов представлены в таблице 8.6.5.
Ожидаемый доход бюджета в январе 2006 г. составит 126,01млн. р., в феврале 70,93 млн.р.
Качество построенной модели оценивается как хорошее.
4. Построить модель регрессии с включением фактора времени и фиктивных переменных. Для всех построенных моделей с помощью средней относительной ошибки аппроксимации оценить их качество и дать прогноз на следующие два периода.
Прогнозирование по модели регрессии
с включением фактора времени и фиктивных переменных
Спрогнозируем объем производства с помощью модели регрессии с включением фактора времени и фиктивных переменных. Модель для помесячной динамики имеет вид:
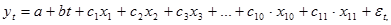
где 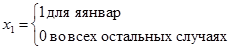
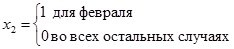
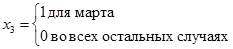
. 
Занесем значение фиктивных переменных и фактора времени в таблицу (таблица 8.6.7).
Таблица 8.6.7 - Исходные данные для расчета параметров уравнения регрессии с фиктивными переменными во временном ряду доходов бюджета, (млн.р.)
5 задание
| Годы | |||
| y | x | ||
| 1 | 315,90 | 5,90 | |
| 2 | 331,00 | 6,90 | |
| 3 | 339,60 | 7,90 | |
| 4 | 363,80 | 9,30 | |
| 5 | 380,00 | 11,00 | |
| 6 | 389,30 | 11,90 | |
| 7 | 411,70 | 13,30 | |
| 8 | 431,60 | 14,30 | |
| 9 | 448,50 | 15,40 | |
| 10 | 462,54 | 16,79 | |
| 11 | 479,23 | 18,02 | |








