Типовые динамические звенья систем

Дата: 2025-06-02; Просмотры: 8
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Лабораторная работа № 2

 

ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ СИСТЕМ

АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

1. ЦЕЛЬ РАБОТЫ

Исследование переходных характеристик и динамических свойств типовых звеньев систем автоматического управления.

 

2. УКАЗАНИЯ К САМОСТОЯТЕЛЬНОЙ РАБОТЕ

При подготовке к лабораторной работе необходимо изучить тему: «Типовые динамические звенья» по литературе [1], [2]. Составить схемы моделей динамических звеньев в соответствии с вариантом задания.

 

3. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Типовыми динамическими звеньями называются простейшие составные части систем автоматического управления, поведение которых описывается обыкновенными дифференциальными уравнениями не выше 2-ого порядка:

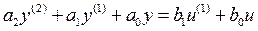, (2.1)

где y и u – соответственно выходная переменная и управляющее воздействие звена; ai и bi – постоянные коэффициенты.

С использованием оператора дифференцирования 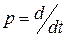уравнение (2.1) имеет вид:

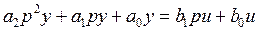, (2.2)

Определяем передаточную функцию W ( p ) звена, учитывая при этом, что начальные условия для уравнения (2.2) нулевые

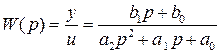(2.3)

Один из способов моделирования систем заключается в представлении преобразования “вход-выход” в виде комплексной передаточной функции:

,

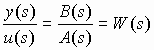которая получается путем применения преобразования Лапласа к (2.2) при начальных нулевых условиях. Здесь s - комплексная переменная. Связь между операторной и комплексной передаточными функциями можно записать в виде

.

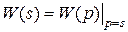Динамические свойства звеньев определяются по их реакции на типовое входное воздействие. Наиболее простым типовым воздействием является единичная ступенчатая функция 1(t), удовлетворяющая условиям

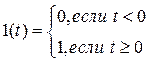. (2.4)

Одной из реакций звена является переходная характеристика h ( t ) – изменение выходной переменной во времени при подаче на вход звена единичной ступенчатой функции 1( t ). Переходная характеристика представляет переход звена (системы) от одного равновесного состояния или установившегося режима к другому.

По графику h ( t ) можно определить математическую модель исследуемого динамического звена и его параметры.

Интегрирующее звено

Описывается уравнениями:

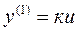или 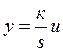, (2.5)

где k – постоянный коэффициент.

Переходная характеристика звена

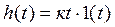(2.6)