Численное решение задачи Коши для дифференциальных уравнений.

Дата: 2025-06-02; Просмотры: 8
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

ЛАБОРАТОРНАЯ РАБОТА 6 .

ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.

Теоретический материал к данной теме содержится в [1, глава 14].

Отчет по лабораторной работе должен содержать следующие материалы по каждой задаче: 1) постановка задачи; 2) необходимый теоретический материал; 3) решение поставленной задачи; 4) анализ полученных результатов; 5) графический материал (если необходимо); 6) тексты программ.

Варианты заданий к задачам 6.1-6.2 даны в ПРИЛОЖЕНИИ 6.А.

 

Задача 6.1. Найти приближенное решение задачи Коши для обыкновенного дифференциального уравнения (ОДУ) 1 порядка с точностью .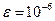

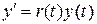
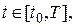(1)

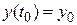
ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:

1. Найти аналитическое решение задачи (см. ПРИЛОЖЕНИЕ 6. B ).

2. Составить программу вычисления решения методом Эйлера. Найти решение задачи с постоянным шагом 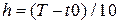. Построить график погрешности.

3. Используя встроенную функцию rkfixed пакета MATHCAD, найти приближенное решение задачи Коши с шагом 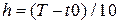по методу Рунге-Кутты 4 порядка точности. Построить график погрешности.

4.Составить программу вычисления решения методом Эйлера с заданной точностью, используя правило Рунге. Найти решение задачи с точностью 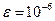, число точек N и шаг, при котором точность достигается. Построить график решения.

5. Сравнить полученные результаты.

6. Оформить отчет по задаче.

 

Задача 6.2. Задача Коши для ОДУ 1 порядка

 

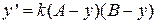
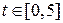(2)

.

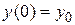описывает химическую реакцию взаимодействия двух веществ. Здесь А и В - первоначальная концентрация первого и второго веществ , 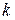- скорость химической реакции, 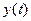описывает концентрацию вещества C, образовавшегося в результате химической реакции в момент времени t . Найти приближенное решение задачи и вычислить указанные в варианте величины.

 

ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:

 

1. Используя встроенную функцию rkfixed пакета MATHCAD, найти приближенное решение задачи Коши с шагом h=0.5 по методу Рунге-Кутты 4 порядка точности (см. ПРИЛОЖЕНИЕ 6. B ) при значении .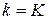

2. Увеличивая значение 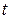, экспериментально найти такое значение TN , при котором процесс химической реакции устанавливается. За момент TN принять то значение 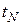, при котором: .

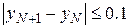3. На отрезке 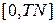построить точечный график найденного решения 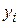, i =0.. N.

4. Найти скорость химической реакции 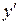в точках 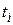, i =0.. N и построить точечный график 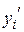на отрезке .

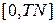5. Вычислить энергию химической реакции по формуле: 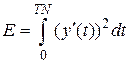. Интеграл вычислить формуле индивидуального варианта .

6. Задать множество значений параметра 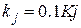, j=1..10 . Для каждого значения параметра найти приближенное решение задачи Коши (2) методом, указанным в индивидуальном варианте, на отрезке по времени 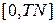с шагом h=0.1.

7. Для каждого полученного решения вычислить интеграл 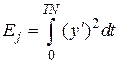и определить значение параметра 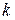, соответствующее максимальному значению интеграла.

8. Построить графики найденных решений 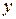, графики скоростей реакции 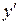, при разных значениях параметра .

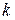ПРИЛОЖЕНИЕ 6.A

ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 6

ВНИМАНИЕ! Номер варианта 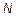для лабораторных работ вычисляется по следующей формуле:

 

1) 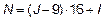для групп 9–11;

2) 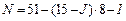для групп 12–15

(здесь 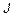— номер группы, а 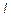— индивидуальный номер студента по журналу).

Примечание. Если полученный номер 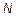получился больше значения 50, то принять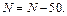

Если полученный номер 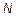получился меньше 1, то принять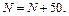

Таблица к задаче 6.1

N 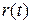y0 t0 T N 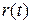y0 t0 T
6.1.1 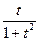1 0 2 6.1.26 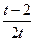-0.607 -1 1
6.1.2 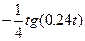1 0 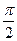6.1.27 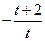0.368 1 2
6.1.3 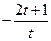0.135 1 2 6.1.28 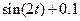0.607 0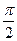
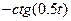
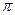
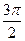
6.1.4 1 6.1.29 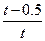2.332 0.5 1.5
6.1.5 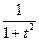1 0 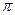6.1.30 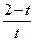0.152 0.5 2
6.1.6 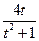0.1 0 2 6.1.31 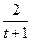0.368 0 2
6.1.7 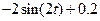e 0 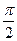6.1.32 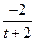0.25 0 2
6.1.8 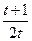0.908 0.5 2 6.1.33 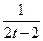1 2 4
6.1.9 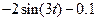1.948 0 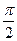6.1.34 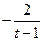1 2 4
6.1.10 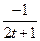1.414 0 2 6.1.35 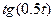1 0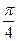
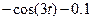
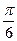
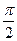
6.1.11 0.68 6.1.36 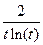1 e 2e
6.1.12 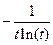1 e 2e 6.1.37 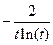1 e 2e
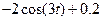
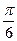
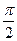
6.1.13 0.57 6.1.38 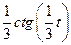1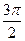
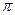
6.1.14 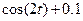1.783 0 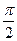6.1.39 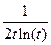1 e 2e
6.1.15 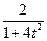1 0 3 6.1.40 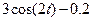3.83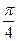
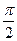
6.1.16 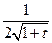e 0 2 6.1.41 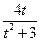3 0 5
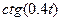
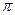
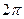
6.1.17 1 6.1.42 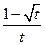2 0 1
6.1.18 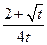4 0 2 6.1.43 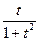1 0 2
6.1.19 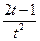1 1 3 6.1.44 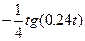1 0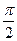
6.1.20 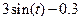2 0 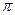6.1.45 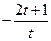0.135 1 2
6.1.21 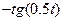1 0 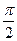6.1.46 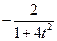1 0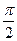
6.1.22 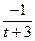0.5 1 2 6.1.47 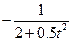1 0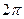
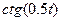
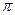
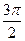
6.1.23 1 6.1.48 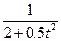1 0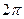
6.1.24 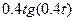1 0 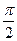6.1.49 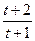0.303 -0.5 0.5
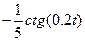
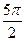
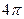
6.1.25 1 6.1.50 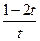0.135 1 3

 

Таблица к задаче 6.2

N y0 A B K N y0 A B K
6.2.1 0 400 190 0.001 6.2.26 0 620 300 0.001
6.2.2 0 600 430 0.00015 6.2.27 0 460 280 0.005
6.2.3 0 10 100 0.001 6.2.28 0 200 20 0.0001
6.2.4 50 370 240 0.001 6.2.29 15 75 25 0.0002
6.2.5 0 560 340 0.001 6.2.30 0 720 340 0.001
6.2.6 0 50 20 0.15 6.2.31 0 50 20 0.15
6.2.7 0 450 320 0.005 6.2.32 0 450 320 0.005
6.2.8 0 200 20 0.0001 6.2.33 0 200 20 0.0001
6.2.9 70 700 230 0.0003 6.2.34 70 700 230 0.0003
6.2.10 0 480 250 0.001 6.2.35 50 480 250 0.001
6.2.11 0 430 180 0.001 6.2.36 0 450 150 0.001
6.2.12 0 560 380 0.015 6.2.37 50 500 380 0.015
6.2.13 0 25 135 0.002 6.2.38 0 15 155 0.002
6.2.14 5 240 80 0.001 6.2.39 10 250 80 0.001
6.2.15 0 660 240 0.001 6.2.40 20 660 200 0.001
6.2.16 0 350 200 0.15 6.2.41 0 350 150 0.15
6.2.17 0 410 300 0.005 6.2.42 0 110 300 0.005
6.2.18 0 200 20 0.0001 6.2.43 0 200 10 0.0001
6.2.19 70 700 230 0.0002 6.2.44 70 700 230 0.0002
6.2.20 0 680 380 0.001 6.2.45 0 680 380 0.001
6.2.21 0 420 160 0.002 6.2.46 30 420 140 0.002
6.2.22 0 440 160 0.002 6.2.47 0 440 120 0.002
6.2.23 0 650 410 0.016 6.2.48 0 450 680 0.016
6.2.24 0 10 100 0.001 6.2.49 0 100 15 0.001
6.2.25 30 310 280 0.001 6.2.50 30 610 280 0.001
Номер варианта 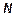Метод решения задачи Коши Метод вычисления интеграла
1, 11, 21, 31, 41 Эйлера-Коши Трапеций
2, 12, 22, 32, 42 Усовершенствованный Эйлера Центральных прямоугольников
3, 13, 23, 33, 43 Рунге-Кутты 3-го порядка (I) Симпсона
4, 14, 24, 34, 44 Экстраполяционный метод Адамса 2-го порядка Трапеций
5, 15, 25, 35, 45 Метод разложения по Тейлору 2-го порядка Правых прямоугольников
6, 16, 26, 36, 46 Рунге-Кутты 3-го порядка (III) Симпсона
7, 17, 27, 37, 47 Интерполяционный метод Адамса 2-го порядка Центральных прямоугольников
8, 18,28, 38, 48 Экстраполяционный метод Адамса 3-го порядка Трапеций
9, 19, 29, 39, 49 Рунге-Кутты 3-го порядка (II) Левых прямоугольников
10, 20, 30, 40, 50 Неявный метод Эйлера Симпсона

ПРИЛОЖЕНИЕ 6.В

 

Рассмотрим пример решения задачи 9.1

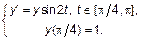
Заданное дифференциальное уравнение решается методом разделения переменных:

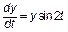
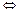
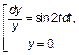
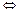
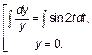
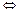
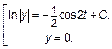
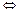
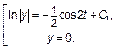
Полученное общее решение (множество всех решений) исходного ОДУ можно записать одной формулой

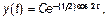где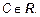

Для определения постоянной 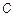воспользуемся начальным условием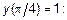

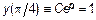
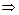
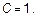
Таким образом, аналитическое решение задачи Коши имеет вид: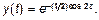

ПРИЛОЖЕНИЕ 6. C

I. Правило Рунге практической оценки погрешности решения задачи Коши для ОДУ 1-го порядка (правило двойного пересчета):

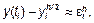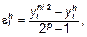
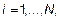
где 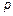— порядок метода (вычисления ведутся в узлах сетки ).

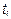Уточненное решение вычисляется по формуле: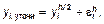

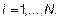
II . Расчетные формулы методов решения задачи Коши для ОДУ 1-го порядка:

1. Метод разложения по формуле Тейлора:

2-го порядка: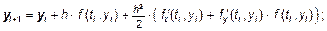

2. Модифицированный метод Эйлера 2-го порядка (метод Эйлера-Коши):

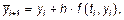
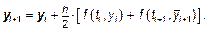
3. Усовершенствованный метод Эйлера 2 порядка:

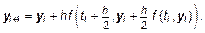
4. Метод Рунге-Кутты 3-го порядка (вариант I): 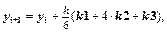где

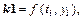
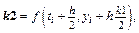
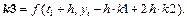
5. Метод Рунге-Кутты 3-го порядка (вариант II): 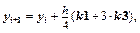где

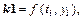
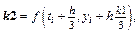
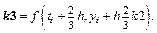
6. Метод Рунге-Кутты 3-го порядка (вариант III): 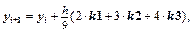где

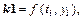
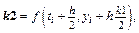
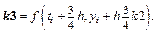
7. Метод Рунге-Кутты 4-го порядка: 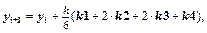где

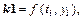
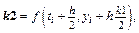
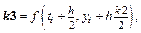
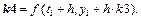
8. Экстраполяционный метод Адамса 2-го порядка:

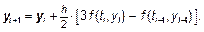
9. Интерполяционный метод Адамса 2-го порядка:

 

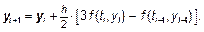
10. Экстраполяционный метод Адамса 3-го порядка:

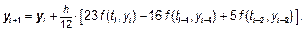
ЛИТЕРАТУРА

1. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высшая школа, 2003.