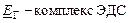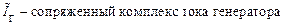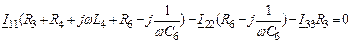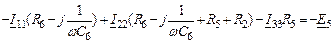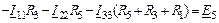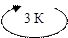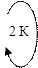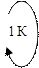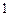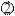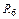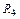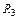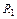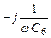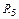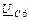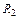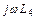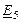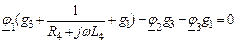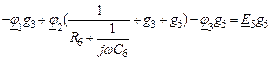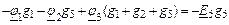Практика 2. Основы символического метода анализа цепей синусоидального тока
2.1 Синусоидальная ЭДС и представление в виде комплекса
Пример 1. Напряжение действующее в домашней розетке можно записать в следующем виде: 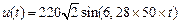 ,
,
220-действующее значение (Вольт)
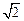 -коэффициент амплитуды для синусоидальной функции
-коэффициент амплитуды для синусоидальной функции
50-частота (Гц)
t-время
Данному синусоидальному напряжению можно поставить в соответствие два комплекса:
1. 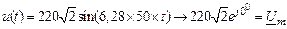 (комплексная амплитуда)
(комплексная амплитуда)
2. 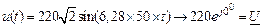 (комплекс действующего значения).
(комплекс действующего значения).
Можно работать с любым из этих комплексов. Чаще используют комплекс действующего значения.
Пример 2. Имеются две синусоидальные ЭДС: 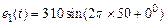 и
и 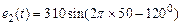 . Требуется получить разность этих двух функций.
. Требуется получить разность этих двух функций.
1. Записываем комплексную амплитуду первой ЭДС: 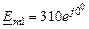
2.Записываем комплексную амплитуду второй ЭДС: 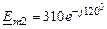
3. Используя программу Mathcad, получаем:

Результирующая ЭДС: 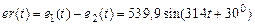
2.2 Запись уравнений по законам Кирхгофа, методам контурных токов и узловых потенциалов
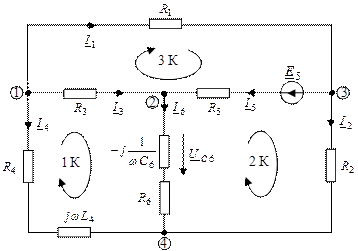
Пример 3. Для схемы, изображенной на рис.1:
1. Записать систему уравнений по законам Кирхгофа для мгновенных значений.
2. Создать расчетную модель для символического метода расчета схемы
3. Записать систему уравнений по законам Кирхгофа в символической форме.
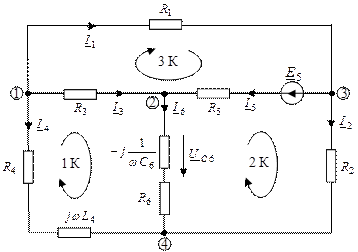
4. Записать систему уравнений по методу контурных токов в символической форме.
5. Записать систему уравнений по методу узловых потенциалов в символической форме.
            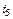 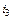 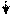 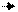 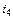    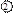   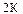   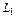  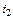 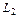 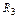 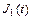  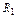 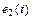 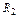 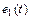 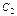                  
|
| Рис.1. Схема примера 3. |
Система уравнений по законам Кирхгофа для мгновенных значений
| 1-ый узел | 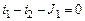
|
| 2-ой узел | 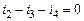
|
| 3-ий узел | 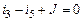
|
| 1-ый контур | 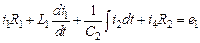
|
| 2-ой контур | 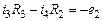
|
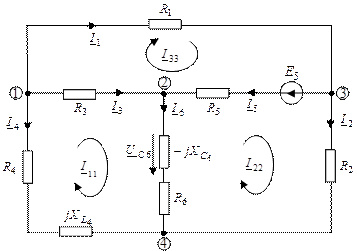
Расчетная модель схемы для символического метода
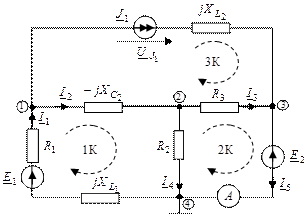 |
|
| ||
| Рис.2. Расчетная модель. Уравнения по законам Кирхгофа в символической форме | ||
| 1-ый узел |
| |
| 2-ой узел |
| |
| 3-ий узел |
| |
| 1-ый контур |
| |
| 2-ой контур |
| |
Уравнения по методу контурных токов в символической форме:
| 1-ый контур | 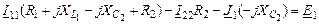
|
| 2-ой контур | 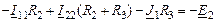
|
Уравнения по методу узловых потенциалов в символической форме.
Примем потенциал 4-го узла равным нулю. Тогда потенциал 3-го узла равен: 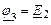 . Составляем два уравнения:
. Составляем два уравнения:
| 1-ый узел | 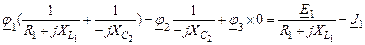
|
| 2-ой узел | 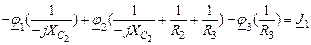
|
Зная величины потенциалов , можно рассчитать токи в ветвях, используя закон Ома и закон Ома для участка цепи с ЭДС.
|
|
| 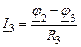
| ||
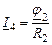
|
|
| ||
Для проверки правильности анализа составляется баланс мощности.
Мощность источников равна сумме мощностей отдельных источников: 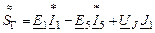
Мощность нагрузки равна сумме мощностей отдельных элементов: 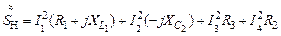 . Должно выполнятся условие:
. Должно выполнятся условие: 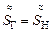
Пример 4. Для схемы, изображенной на рис.3:
|
| Рис.4. Схема примера 4 |
1. Создать расчетную модель для символического метода расчета схемы
2. Записать систему уравнений по законам Кирхгофа в символической форме.
3. Записать систему уравнений по методу контурных токов в символической форме.
4. Записать систему уравнений по методу узловых потенциалов в символической форме.
  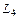  
|
| Рис.5. Схема для анализа символическим методом |
Уравнения по законам Кирхгофа в символическом виде:
| 1-ый узел | 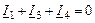
|
| 2-ой узел | 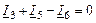
|
| 3-ий узел | 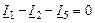
|
| 1-ый контур | 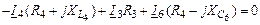
|
| 2-ой контур | 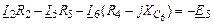
|
| 3-ий контур | 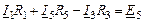
|
Уравнения по методу контурных токов в символическом виде:
| 1-ый контур | 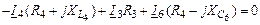
|
| 2-ой контур | 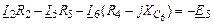
|
| 3-ий контур | 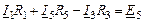
|
Рис.7. Расчетная модель схемы для примера 3.
Пример 4. Рассчитать токи в схеме , показанной на рис.8.
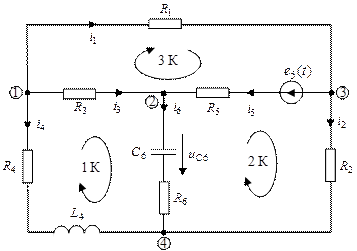
Повторение-мать учения Запишите систему уравнений по законам Кирхгофа для мгновенных значений:
Так как в схеме действует синусоидальная ЭДС, то для расчета используем символический метод. На рис.9 изображена расчетная модель.
Система уравнений по законам Кирхгофа в символической форме имеет вид:
Ниже показан расчет данной системы в программе Mathcad.
Обратите внимание на проверку расчета по балансу мощности: Мощность нагрузки: Мощность генератора
Проведем расчет схемы с использованием метода контурных токов. Рассмотрим схему, показанную на рис.10.
Записываем систему уравнений по методу контурных токов:
Ниже показан расчет данной системы в программе Mathcad. Следует заметить, что это фрагмент общей программы по расчету схемы, изображенной на рис.10. Значения сопротивлении и ЭДС были определены ранее, при расчеты схемы по законам Кирхгофа.
Проведем расчета схемы с использованием метода узловых потенциалов. Записываем систему уравнений по данному методу.
Примем потенциал 4-го узла равным нулю. Записываем систему уравнений по методу узловых потенциалов:
Ниже показан расчет данной системы в программе Mathcad.
|
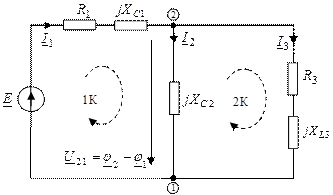
Пример 5. Для схемы, изображенной на рис.12:
1. Записать выражение для входного сопротивления относительно зажимов ЭДС
2. Записать систему уравнений по законам Кирхгофа в символической форме.
3. Построить качественную векторную диаграмму
|
| Рис.12. Схема примера 5 |
1. Сопротивления 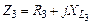 и
и 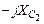 соединены параллельно. Их общее сопротивление определяется выражением:
соединены параллельно. Их общее сопротивление определяется выражением: 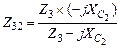
2. Комплекс входного сопротивления будет определяться выражением:
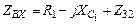
3. Записываем комплекс тока генератора, используя закон Ома: 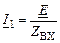
4. Находим напряжение 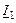
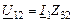
5. Находим 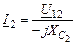 и
и 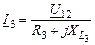
Записываем уравнения по законам Кирхгофа:
| 1-ый узел | 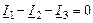
|
| 1-ый контур | 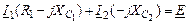
|
| 2-ой контур | 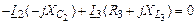
|
Построим качественную векторную диаграмму. Такие диаграммы строится с использованием уравнений по законам Кирхгофа и Ома. Важно выбрать вектор с которого начинается построение. Нельзя начинать с вектора тока на входе схемы ( 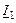 ). Лучше с тока который протекает по большему числу элементов, в данном случае с тока
). Лучше с тока который протекает по большему числу элементов, в данном случае с тока 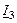 . Этот вектор построен первым. Далее строятся вектора в соответствии с уравнениями записанными по законам Кирхгофа.
. Этот вектор построен первым. Далее строятся вектора в соответствии с уравнениями записанными по законам Кирхгофа.

|
| Рис.12. Качественная векторная диаграмма для схемы по рис.12 |









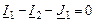
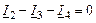
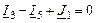
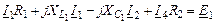
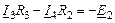
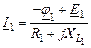
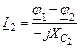
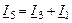
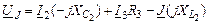
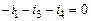
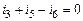
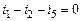
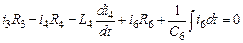
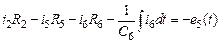
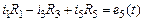
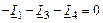
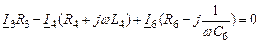
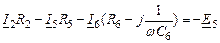
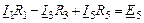




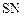 считается для каждого элемента по формуле
считается для каждого элемента по формуле 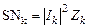 , где
, где 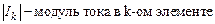 ,
, 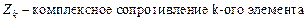 ,
,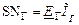 , где
, где